Da, to je i mene zanimalo. Evo što sam otkrio googlajući.
Najvažniji korak u dokazivanju te tvrdnje je zapravo pokazati da proizvoljan beskonačan skup [latex]A[/latex] možeš razdijeliš na dva podjednaka dijela koja će oba biti ekvipotentna početnom. Nakon toga dokaz možeš završit na razne načine. Najlakše crtanjem sličica.
Npr. Jasno je [latex]k(A \setminus B) \leq k(A)[/latex]. Kako je [latex]A \setminus B[/latex] beskonačan onda ga razdijeliš u dva skupa njemu ekvipotentna. I sada lako imaš [latex]k(A \setminus B) \geq(A)[/latex] jer bijektivno možeš poslat [latex]A \setminus B[/latex] u prvu polovicu, a injektivno [latex]B[/latex] u drugu polovicu koja je veća od [latex]B[/latex]. CSB daje jednakost.
Ostaje naravno pitanje kako "raspoloviti" beskonačan skup. Na http://planetmath.org/?op=getobj&from=objects&id=11739 ima dokaz da za sve beskonačne kardinale vrijedi idempotentnost. Iz toga lako izvučeš da su za beskonačni skup [latex]A[/latex] skupovi [latex]\{0,1\} \times A[/latex] i [latex]A[/latex] ekvipotentni, pa ti to daje jedno raspolavljanje. Naravno ostaje problem gornjeg dokaza, jer koristi uređaj na kardinalima (ordinalima) pa ga još ne razumijemo :D
Da. Sad kad sam se ja ovako raspisao, baš bi bilo lijepo kad bi neki asistent ili netko drugi dao kratki dokaz u jednoj liniji. :silly:
Da, to je i mene zanimalo. Evo što sam otkrio googlajući.
Najvažniji korak u dokazivanju te tvrdnje je zapravo pokazati da proizvoljan beskonačan skup 
možeš razdijeliš na dva podjednaka dijela koja će oba biti ekvipotentna početnom. Nakon toga dokaz možeš završit na razne načine. Najlakše crtanjem sličica.
Npr. Jasno je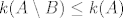 
. Kako je 
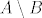beskonačan onda ga razdijeliš u dva skupa njemu ekvipotentna. I sada lako imaš 
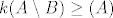jer bijektivno možeš poslat 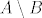u prvu polovicu, a injektivno 
u drugu polovicu koja je veća od . CSB daje jednakost.
Ostaje naravno pitanje kako "raspoloviti" beskonačan skup. Na http://planetmath.org/?op=getobj&from=objects&id=11739 ima dokaz da za sve beskonačne kardinale vrijedi idempotentnost. Iz toga lako izvučeš da su za beskonačni skup skupovi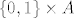 
i ekvipotentni, pa ti to daje jedno raspolavljanje. Naravno ostaje problem gornjeg dokaza, jer koristi uređaj na kardinalima (ordinalima) pa ga još ne razumijemo 
Da. Sad kad sam se ja ovako raspisao, baš bi bilo lijepo kad bi neki asistent ili netko drugi dao kratki dokaz u jednoj liniji. 
_________________
Jedan je smjer očit, a drugi je trivijalan.
