| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
 Postano: 18:03 sub, 27. 3. 2010 Naslov: zadatak matrični zapis lin. op. Postano: 18:03 sub, 27. 3. 2010 Naslov: zadatak matrični zapis lin. op. |
    |
|
|
treba naći matricu operatora A R3->P1 ( sa prostora r 3 u prostor polinoma st<=1)
A(x,y,z)=x+y+z+tx u paru baza { (1,1,0),(1,0,1),(0,0,1) } i { 1+t,1-2t)
zadatak s vježbi al za dz , ako je slučajno netko riješio pa da mi napiše sam riješenje il ak se nekom da riješit bilo bi super :D
treba naći matricu operatora A R3->P1 ( sa prostora r 3 u prostor polinoma st<=1)
A(x,y,z)=x+y+z+tx u paru baza { (1,1,0),(1,0,1),(0,0,1) } i { 1+t,1-2t)
zadatak s vježbi al za dz , ako je slučajno netko riješio pa da mi napiše sam riješenje il ak se nekom da riješit bilo bi super 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:19 sub, 27. 3. 2010 Naslov: Postano: 18:19 sub, 27. 3. 2010 Naslov: |
    |
|
|
e i f kanonske baze za [latex]\mathbb{R}^3[/latex] i [latex]P_1[/latex], e' i f' nekanonske baze.
[latex]A(f,e) = \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & 0 & 0 \end{matrix} \right], I(e,e') = \left[ \begin{matrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 1 \end{matrix} \right], I(f,f') = \left[ \begin{matrix} 1 & 1 \\ 1 & -2 \end{matrix} \right][/latex]
[latex]A(f',e') = I(f',f) \cdot A(f,e) \cdot I(e,e') = I(f,f')^{-1} \cdot A(f,e) \cdot I(e,e') = \left[ \begin{matrix} 1 & 1 \\ 1 & -2 \end{matrix} \right]^{-1} \cdot \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & 0 & 0 \end{matrix} \right] \cdot \left[ \begin{matrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 1 \end{matrix} \right] = \ldots = \frac{1}{3} \cdot \left[ \begin{matrix} 5 & 5 & 2 \\ 1 & 1 & 1 \end{matrix} \right][/latex]
e i f kanonske baze za 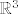 i i 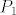 , e' i f' nekanonske baze. , e' i f' nekanonske baze.
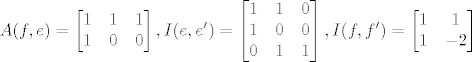
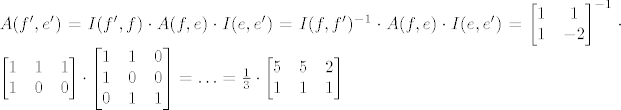
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
 Postano: 10:01 ned, 28. 3. 2010 Naslov: Postano: 10:01 ned, 28. 3. 2010 Naslov: |
    |
|
|
2. Operator B : P2 → P2 zadan je s
B(p)(t) = p(t + 1).
(P2 je prostor polinoma stupnja ≤ 2)
Odredite matriˇcni prikaz operatora B u paru baza
{B(1),B(t),B(t^2)}, {1 − t, 1 − t^2, 1 + t^2}.
jel mi moze neko pomoci odrediti samo ovu bazu u kojoj imamo operator ukljucen..
hvala
2. Operator B : P2 → P2 zadan je s
B(p)(t) = p(t + 1).
(P2 je prostor polinoma stupnja ≤ 2)
Odredite matriˇcni prikaz operatora B u paru baza
{B(1),B(t),B(t^2)}, {1 − t, 1 − t^2, 1 + t^2}.
jel mi moze neko pomoci odrediti samo ovu bazu u kojoj imamo operator ukljucen..
hvala
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 10:53 ned, 28. 3. 2010 Naslov: Postano: 10:53 ned, 28. 3. 2010 Naslov: |
    |
|
|
[latex]e = \{1, t, t^2\}, f = \{B(1), B(t), B(t^2)\} = \{1, 1 + t, 1 + 2 t + t^2\}, g = \{1 - t, 1 - t^2, 1 + t^2\}[/latex]
[latex]B(e) = \left[ \begin{matrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{matrix} \right], I(e,f) = \left[ \begin{matrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{matrix} \right], I(e,g) = \left[ \begin{matrix} 1 & 1 & 1 \\ -1 & 0 & 0 \\ 0 & -1 & 1 \end{matrix} \right][/latex]
[latex]B(g,f) = I(e,g)^{-1} \cdot B(e) \cdot I(e,f) = \ldots = \frac{1}{2} \left[ \begin{matrix} 0 & -2 & -8 \\ 1 & 3 & 7 \\ 1 & 3 & 9 \end{matrix} \right][/latex]
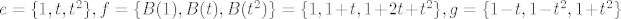

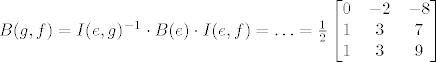
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 17:40 ned, 28. 3. 2010 Naslov: Postano: 17:40 ned, 28. 3. 2010 Naslov: |
    |
|
|
Po formuli u zadatku: B(p)(t) = p(t + 1).
1 je konstanta, tj. ne ovisi o t, pa je B(1)=1. Za t je očito (B(t)=t+1), a i za t^2 (B(t^2)=(t+1)^2=t^2+2t+1).
Za B(e), u i-ti stupac trebaš napisati koeficijente (redom kako se odabrao redosljed u bazi e) rastava [latex]B(e_i)[/latex] ([latex]e_i[/latex] je i-ti element baze e). Malo je neobično govoriti o uređaju u skupu, ali kad su nas već tak naučili... No, u ovom konkretnom slučaju možemo odabrati za bazu [latex]e = \{ 1, t, t^2 \}[/latex]. Tada se naš posao svodi na to da prepišemo koeficijente iz [latex]\{ 1 + 0 \cdot t + 0 \cdot t^2, 1 + 1 \cdot t + 0 \cdot t^2, 1 + 2 \cdot t + 1 \cdot t^2 \}[/latex] u stupce. Ima li nešto nejasno?
Po formuli u zadatku: B(p)(t) = p(t + 1).
1 je konstanta, tj. ne ovisi o t, pa je B(1)=1. Za t je očito (B(t)=t+1), a i za t^2 (B(t^2)=(t+1)^2=t^2+2t+1).
Za B(e), u i-ti stupac trebaš napisati koeficijente (redom kako se odabrao redosljed u bazi e) rastava 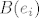 ( (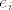 je i-ti element baze e). Malo je neobično govoriti o uređaju u skupu, ali kad su nas već tak naučili... No, u ovom konkretnom slučaju možemo odabrati za bazu je i-ti element baze e). Malo je neobično govoriti o uređaju u skupu, ali kad su nas već tak naučili... No, u ovom konkretnom slučaju možemo odabrati za bazu 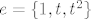 . Tada se naš posao svodi na to da prepišemo koeficijente iz . Tada se naš posao svodi na to da prepišemo koeficijente iz 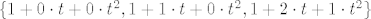 u stupce. Ima li nešto nejasno? u stupce. Ima li nešto nejasno?
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 19:16 ned, 28. 3. 2010 Naslov: Postano: 19:16 ned, 28. 3. 2010 Naslov: |
    |
|
|
Misliš vjerojatno pod (ii) :D
Možeš to na više načina. Jedan je da nađeš prikaz od A u kanonskoj bazi, pa onda to pomnožiš s (1,1,2) (mislim na vektor-stupac). Drugi je da (1,1,2) prikažeš u bazi f pa pomnožiš s A(g,f) (ili s A(f)), pa onda to moraš vratiti u prikaz u kanonskoj bazi. Meni se nekako prvi način čini bolji. Prvo probaj sam/a, pa javi ako nejde.
Edit: Kad se zapravo razmisli, dobi se da su to jedan te isti način :oops:, što je i nekako prirodno za očekivati :doh:. Dakle, formula bi bila [latex](Ax)(e) = I(e,g) \cdot A(g,f) \cdot I(f,e) \cdot x(e)[/latex] u oba "slučaja". Pravi drugi način bi bio da se iskoristi A(f) iz (i) dijela zadatka.
Misliš vjerojatno pod (ii) 
Možeš to na više načina. Jedan je da nađeš prikaz od A u kanonskoj bazi, pa onda to pomnožiš s (1,1,2) (mislim na vektor-stupac). Drugi je da (1,1,2) prikažeš u bazi f pa pomnožiš s A(g,f) (ili s A(f)), pa onda to moraš vratiti u prikaz u kanonskoj bazi. Meni se nekako prvi način čini bolji. Prvo probaj sam/a, pa javi ako nejde.
Edit: Kad se zapravo razmisli, dobi se da su to jedan te isti način  , što je i nekako prirodno za očekivati , što je i nekako prirodno za očekivati  . Dakle, formula bi bila . Dakle, formula bi bila 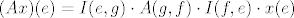 u oba "slučaja". Pravi drugi način bi bio da se iskoristi A(f) iz (i) dijela zadatka. u oba "slučaja". Pravi drugi način bi bio da se iskoristi A(f) iz (i) dijela zadatka.
Zadnja promjena: pmli; 5:45 pon, 29. 3. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 20:21 sub, 3. 4. 2010 Naslov: Postano: 20:21 sub, 3. 4. 2010 Naslov: |
    |
|
|
2. zadatak 2008 A grupa: http://web.math.hr/nastava/la/kolokviji/07-08/la2/kol1a.pdf
Ja sam to rješavao na sljedeći način, zanima me valja li štogod:
[latex]A(f'',e'')=I(f'',f')\cdot A(f',e')\cdot I(e',e'')=
\\
\\ = \left[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{matrix}\right]^{-1} \cdot \left[\begin{matrix} 1 & 1 & 1 & 2 \\ 2 & 0 & 1 & 0 \\ 1 & 1 & 0 & 2 \\ 1 & 1 & 1 & 2 \end{matrix} \right] \cdot \left[ \begin{matrix} 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\0 & 0 & 0 & -1 \\ 0 & 1 & 1 & 1 \end{matrix} \right]^{-1}=...
[/latex]
Prvu bazu za domenu sam označio sa (e'), drugu sa (e''), prvu bazu za kodomenu sa (f'), a drugu sa (f''). Samo me zanima jeli postupak korektan.
Također, za ovaj dio sa izomorfizmom, nisam stoposto siguran na koji način se u ovom zadatku dokaže pa bih molio pomoć.
2. zadatak 2008 A grupa: http://web.math.hr/nastava/la/kolokviji/07-08/la2/kol1a.pdf
Ja sam to rješavao na sljedeći način, zanima me valja li štogod:
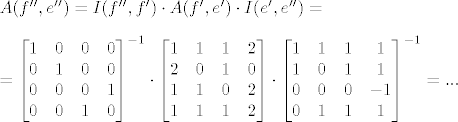
Prvu bazu za domenu sam označio sa (e'), drugu sa (e''), prvu bazu za kodomenu sa (f'), a drugu sa (f''). Samo me zanima jeli postupak korektan.
Također, za ovaj dio sa izomorfizmom, nisam stoposto siguran na koji način se u ovom zadatku dokaže pa bih molio pomoć.
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
|
















