| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
rozenheim
Forumaš(ica)

Pridružen/a: 04. 09. 2006. (16:39:45)
Postovi: (2)16
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 21:43 sri, 1. 11. 2006 Naslov: Re: Tenzorski produkt Postano: 21:43 sri, 1. 11. 2006 Naslov: Re: Tenzorski produkt |
    |
|
|
[quote="rozenheim"]"Tenzorski produkt vektorskih prostora X i Y je uredjen par (T, t) gdje je T v.p. nad F, a t:XxY->T bilinearno preslikavanje sa svojstvom:
za svaki V v.p. nad F i svako bilinearno preslikavanje Psi:XxY->V postoji jedinstveno (linearno preslikavanje, operator?) fi:T->V t.d. Psi=fi o t (o = komponirano).
Da li to znaci da je i (V, Psi) tenzorski produkt v.p. X i Y ?[/quote]
Ako sam dobro shvatio, ti pitaš da li je svaki vektorski prostor [latex]V[/latex] sa blilinearnim preslikavanjem [latex]\psi : X \times Y \rightarrow V[/latex] tenzorski produkt od [latex]X[/latex] i [latex]Y[/latex]? Ako to pitaš, onda je odgovor ne.
Tenzorski produkt od [latex]X[/latex] i [latex]Y[/latex] je specijalni par par [latex](T, t)[/latex] koji zadovoljava gornje univerzalno svojstvo. Lako pokažeš da iz univerzalog svojstva slijedi da su svaka dva tenzorska produkta [latex](T,t')[/latex] i [latex](T',t')[/latex] nužno izomorfna (npr. kao vekt. prostori), pa specijalno slijedi da definicija tenzorskog produkta nije trivijalna, tj da ju ne zadovoljava svaki par [latex](V,\psi)[/latex].
| rozenheim (napisa): | "Tenzorski produkt vektorskih prostora X i Y je uredjen par (T, t) gdje je T v.p. nad F, a t:XxY→T bilinearno preslikavanje sa svojstvom:
za svaki V v.p. nad F i svako bilinearno preslikavanje Psi:XxY→V postoji jedinstveno (linearno preslikavanje, operator?) fi:T→V t.d. Psi=fi o t (o = komponirano).
Da li to znaci da je i (V, Psi) tenzorski produkt v.p. X i Y ? |
Ako sam dobro shvatio, ti pitaš da li je svaki vektorski prostor 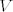 sa blilinearnim preslikavanjem sa blilinearnim preslikavanjem 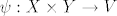 tenzorski produkt od tenzorski produkt od  i i 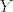 ? Ako to pitaš, onda je odgovor ne. ? Ako to pitaš, onda je odgovor ne.
Tenzorski produkt od  i i 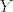 je specijalni par par je specijalni par par 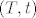 koji zadovoljava gornje univerzalno svojstvo. Lako pokažeš da iz univerzalog svojstva slijedi da su svaka dva tenzorska produkta koji zadovoljava gornje univerzalno svojstvo. Lako pokažeš da iz univerzalog svojstva slijedi da su svaka dva tenzorska produkta 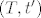 i i 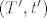 nužno izomorfna (npr. kao vekt. prostori), pa specijalno slijedi da definicija tenzorskog produkta nije trivijalna, tj da ju ne zadovoljava svaki par nužno izomorfna (npr. kao vekt. prostori), pa specijalno slijedi da definicija tenzorskog produkta nije trivijalna, tj da ju ne zadovoljava svaki par 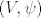 . .
|
|
| [Vrh] |
|
rozenheim
Forumaš(ica)

Pridružen/a: 04. 09. 2006. (16:39:45)
Postovi: (2)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 16:33 sri, 28. 4. 2010 Naslov: Postano: 16:33 sri, 28. 4. 2010 Naslov: |
    |
|
|
Imam problem s jednim dijelom dokaza slijedeće propozicije:
Neka su X, Y vektorski prostori, [latex]t\in X\oplus Y[/latex] i [latex]\{e_i~|~i\in I\}[/latex] baza za X, gdje je I indeksni skup. Tada postoji jedinstven konačan podskup [latex]I_0\subset I[/latex] i jedinstven skup [latex]\{y_i | i\in I_0\}\subset Y[/latex] td. je [latex]t=\sum_{i\in I_0}e_i\oplus y_i[/latex].
Dokaz: neka je [latex]\{f_j~|~j\in J\}[/latex] baza za Y. Tada je za neki konačni [latex]J_0\subset J[/latex],
[latex]\displaystyle t=\sum_{i\in I_0,~j\in J_0}\lambda_{ij}(e_i \oplus f_j)=\sum_{i\in I_0}e_i \oplus (\sum_{j\in J_0}\lambda_{ij}f_j)[/latex]
i stavimo [latex]y_i=\sum_{j\in J_0}\lambda_{ij}f_j[/latex]. Time je egzistencija dokazana.
Što se tiče jedinstvenosti, u bilješkama stoji da jedinstvenost slijedi iz slijedeće propozicije:
Neka je [latex]\{x_1,\dots,x_n\}[/latex] linearno nezavisan skup u X, te neka je [latex]\sum_{i=1}^n x_i \oplus y_i =0[/latex]. Tada je [latex]y_i=0, i=1,\dots, n[/latex] (analogno vrijedi ako x zamijenimo sa y).
Kako istovremeno time osiguravamo da su [latex]I_0[/latex] i još neki možebitni indeksni skup [latex]I_0'[/latex] jednaki i da je [latex]\{y_i | i\in I_0\}[/latex]=[latex]\{y'_i | i\in I_0'\}[/latex]?
Imam problem s jednim dijelom dokaza slijedeće propozicije:
Neka su X, Y vektorski prostori, 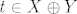 i i 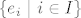 baza za X, gdje je I indeksni skup. Tada postoji jedinstven konačan podskup baza za X, gdje je I indeksni skup. Tada postoji jedinstven konačan podskup 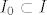 i jedinstven skup i jedinstven skup 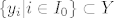 td. je td. je 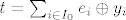 . .
Dokaz: neka je 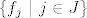 baza za Y. Tada je za neki konačni baza za Y. Tada je za neki konačni 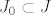 , ,
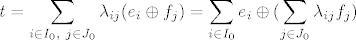
i stavimo 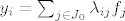 . Time je egzistencija dokazana. . Time je egzistencija dokazana.
Što se tiče jedinstvenosti, u bilješkama stoji da jedinstvenost slijedi iz slijedeće propozicije:
Neka je  linearno nezavisan skup u X, te neka je linearno nezavisan skup u X, te neka je 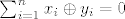 . Tada je . Tada je 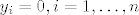 (analogno vrijedi ako x zamijenimo sa y). (analogno vrijedi ako x zamijenimo sa y).
Kako istovremeno time osiguravamo da su 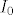 i još neki možebitni indeksni skup i još neki možebitni indeksni skup 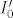 jednaki i da je jednaki i da je 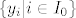 = =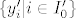 ? ?
_________________
The Dude Abides
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 4:49 čet, 29. 4. 2010 Naslov: Postano: 4:49 čet, 29. 4. 2010 Naslov: |
    |
|
|
[quote="goranm"]Imam problem s jednim dijelom dokaza slijedeće propozicije:
Neka su X, Y vektorski prostori, [latex]t\in X\oplus Y[/latex] i [latex]\{e_i~|~i\in I\}[/latex] baza za X, gdje je I indeksni skup. Tada postoji jedinstven konačan podskup [latex]I_0\subset I[/latex] i jedinstven skup [latex]\{y_i | i\in I_0\}\subset Y[/latex] td. je [latex]t=\sum_{i\in I_0}e_i\oplus y_i[/latex].
Dokaz: neka je [latex]\{f_j~|~j\in J\}[/latex] baza za Y. Tada je za neki konačni [latex]J_0\subset J[/latex],
[latex]\displaystyle t=\sum_{i\in I_0,~j\in J_0}\lambda_{ij}(e_i \oplus f_j)=\sum_{i\in I_0}e_i \oplus (\sum_{j\in J_0}\lambda_{ij}f_j)[/latex]
i stavimo [latex]y_i=\sum_{j\in J_0}\lambda_{ij}f_j[/latex]. Time je egzistencija dokazana.
Što se tiče jedinstvenosti, u bilješkama stoji da jedinstvenost slijedi iz slijedeće propozicije:
Neka je [latex]\{x_1,\dots,x_n\}[/latex] linearno nezavisan skup u X, te neka je [latex]\sum_{i=1}^n x_i \oplus y_i =0[/latex]. Tada je [latex]y_i=0, i=1,\dots, n[/latex] (analogno vrijedi ako x zamijenimo sa y).
Kako istovremeno time osiguravamo da su [latex]I_0[/latex] i još neki možebitni indeksni skup [latex]I_0'[/latex] jednaki i da je [latex]\{y_i | i\in I_0\}[/latex]=[latex]\{y'_i | i\in I_0'\}[/latex]?[/quote]
[latex] I_{0}, I_0'[/latex] su podskupovi skupa I, koji je linearno nezavisan. Ako se t moze napisati na dva nacina, kao [latex]t=\sum_{i\in I_0}e_i \otimes y_{i}=\sum_{i\in I_0'}e_i \otimes y'_{i}[/latex], onda prebacivanjem svega na istu stranu (tj pisanjem t-t=0) i koristenjem ovve tvrdnje koju si napisao dobijes da je koeficijent od t-t uz svaki e_{i} iz I_{0}UI'_{0} jednak nula. Dakle, ako se i pojavljuje samo u I_{0} a ne u I'_{0}, onda je y_{i}=0, pa ga mozemo izbaciti. Isto tako ako se pojavljuje samo u I'_{0}. Dakle, wlog I_{0}=I'_{0}. Nakon toga slijedi da je koeficijent uz svaki e_{i} takav da se i pojavljuje u I_{0} i u I'_{0} jednak nula, tj y_{i}-y'_{i}=0.
| goranm (napisa): | Imam problem s jednim dijelom dokaza slijedeće propozicije:
Neka su X, Y vektorski prostori, 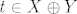 i i 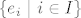 baza za X, gdje je I indeksni skup. Tada postoji jedinstven konačan podskup baza za X, gdje je I indeksni skup. Tada postoji jedinstven konačan podskup 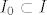 i jedinstven skup i jedinstven skup 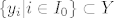 td. je td. je 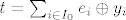 . .
Dokaz: neka je 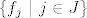 baza za Y. Tada je za neki konačni baza za Y. Tada je za neki konačni 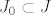 , ,
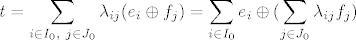
i stavimo 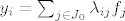 . Time je egzistencija dokazana. . Time je egzistencija dokazana.
Što se tiče jedinstvenosti, u bilješkama stoji da jedinstvenost slijedi iz slijedeće propozicije:
Neka je  linearno nezavisan skup u X, te neka je linearno nezavisan skup u X, te neka je 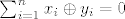 . Tada je . Tada je 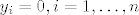 (analogno vrijedi ako x zamijenimo sa y). (analogno vrijedi ako x zamijenimo sa y).
Kako istovremeno time osiguravamo da su 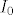 i još neki možebitni indeksni skup i još neki možebitni indeksni skup 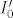 jednaki i da je jednaki i da je 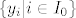 = =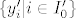 ? ? |
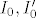 su podskupovi skupa I, koji je linearno nezavisan. Ako se t moze napisati na dva nacina, kao su podskupovi skupa I, koji je linearno nezavisan. Ako se t moze napisati na dva nacina, kao 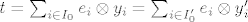 , onda prebacivanjem svega na istu stranu (tj pisanjem t-t=0) i koristenjem ovve tvrdnje koju si napisao dobijes da je koeficijent od t-t uz svaki e_{i} iz I_{0}UI'_{0} jednak nula. Dakle, ako se i pojavljuje samo u I_{0} a ne u I'_{0}, onda je y_{i}=0, pa ga mozemo izbaciti. Isto tako ako se pojavljuje samo u I'_{0}. Dakle, wlog I_{0}=I'_{0}. Nakon toga slijedi da je koeficijent uz svaki e_{i} takav da se i pojavljuje u I_{0} i u I'_{0} jednak nula, tj y_{i}-y'_{i}=0. , onda prebacivanjem svega na istu stranu (tj pisanjem t-t=0) i koristenjem ovve tvrdnje koju si napisao dobijes da je koeficijent od t-t uz svaki e_{i} iz I_{0}UI'_{0} jednak nula. Dakle, ako se i pojavljuje samo u I_{0} a ne u I'_{0}, onda je y_{i}=0, pa ga mozemo izbaciti. Isto tako ako se pojavljuje samo u I'_{0}. Dakle, wlog I_{0}=I'_{0}. Nakon toga slijedi da je koeficijent uz svaki e_{i} takav da se i pojavljuje u I_{0} i u I'_{0} jednak nula, tj y_{i}-y'_{i}=0.
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
|





