|
Valjda nije tajna, pa ću ja napisati. :)
[b]ZADACI:[/b]
[b]1.[/b] Neka je [latex]A[/latex] simetrična invertibilna [latex]n \times n[/latex] [latex]\left(n \geq 2\right)[/latex] matrica s pozitivnim elementima. Označimo sa [latex]z_n[/latex] broj nula u [latex]A^{-1}[/latex].[list]
a) Dokažite da je [latex]z_n \leq n^2 - 2n[/latex].
b) Dokažite da se jednakost u a) postiže. (Dakle, za svaki [latex]n[/latex], a ne samo za neki, npr. [latex]2[/latex] :D)
[/list:u]
[b]2.[/b] Neka je [latex]n \geq 3[/latex] prirodan broj i neka su [latex]a_1,\, a_2,\, \ldots,\, a_n[/latex] različiti prirodni brojevi. Dokažite da postoje različiti indeksi [latex]i[/latex] i [latex]j[/latex] takvi da [latex]a_i + a_j[/latex] ne dijeli niti jedan od brojeva [latex]3a_1,\, 3a_2,\, \ldots,\, 3a_n[/latex].
[b]3.[/b] Izračunajte limes
[latex]\lim\limits_{n \to \infty}{\frac{1}{\sqrt{n}}\int\limits_{1}^{n}{\ln{\left(1+\frac{1}{\sqrt{x}}\right)}\mathrm{d}x}}[/latex].
[b]4.[/b] Neka je [latex]X[/latex] skup od [latex]n \geq 3[/latex] elemenata i neka su [latex]A_1,\, \ldots,\, A_m[/latex] njegovi pravi podskupovi takvi da se svaki par elemenata skupa [latex]X[/latex] zajedno nalazi u točno jednom od tih podskupova. Dokažite da je tada [latex]m \geq n[/latex].
[b]5.[/b] Neka su [latex]a,\, b[/latex] pozitivni realni brojevi takvi da je [latex]a < b[/latex]. Definirajmo rekurzivno nizove [latex]\left(a_n\right)_n[/latex] i [latex]\left(b_n\right)_n[/latex] formulama [latex]a_0=a[/latex], [latex]b_0 = b[/latex],
[latex]a_{n+1}=\frac{a_n + b_n}{2}[/latex], [latex]b_{n+1}=\sqrt{a_{n+1}b_n}[/latex], [latex]n \geq 0[/latex].
Dokažite da je
[latex]\lim\limits_{n \to \infty}{a_n}=\lim\limits_{n \to \infty}{b_n}=\frac{\sqrt{b^2-a^2}}{\arccos{\frac{a}{b}}}[/latex].
Svaki zadatak je nosio 20 bodova, pisalo se 4 sata.
Evo i rezultata, za ljude koji su prošli.
[table]Ime Prezime Zad1 Zad2 Zad3 Zad4 Zad5 Ukupno
Nina Kamčev 20 2 20 20 0 62
Petar Sirković 20 20 15 3 2 60
Melkior Ornik 20 15 0 0 1 36
Ivan Krijan 10 2 19 2 0 33
Luka Rimanić 10 1 0 0 20 31
Filip Barl 10 0 19 0 0 29
Luka Žunić 10 0 15 0 2 27
Branimir Blašković 1 0 20 3 0 24
Ana Kontrec 1 2 20 0 1 24
Nikola Adžaga 10 3 5 2 2 22
Petar Bakić 0 0 20 2 0 22
Željko Kereta 0 0 20 2 0 22
Marko Božić 1 0 20 0 0 21[/table]
Valjda nije tajna, pa ću ja napisati. 
ZADACI:
1. Neka je  simetrična invertibilna simetrična invertibilna 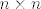  matrica s pozitivnim elementima. Označimo sa matrica s pozitivnim elementima. Označimo sa 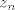 broj nula u broj nula u 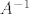 . .
a) Dokažite da je 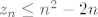 . .
b) Dokažite da se jednakost u a) postiže. (Dakle, za svaki  , a ne samo za neki, npr. , a ne samo za neki, npr.   ) )
2. Neka je 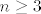 prirodan broj i neka su prirodan broj i neka su 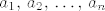 različiti prirodni brojevi. Dokažite da postoje različiti indeksi različiti prirodni brojevi. Dokažite da postoje različiti indeksi  i i 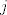 takvi da takvi da 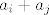 ne dijeli niti jedan od brojeva ne dijeli niti jedan od brojeva 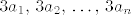 . .
3. Izračunajte limes
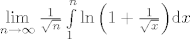 . .
4. Neka je  skup od skup od 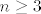 elemenata i neka su elemenata i neka su 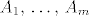 njegovi pravi podskupovi takvi da se svaki par elemenata skupa njegovi pravi podskupovi takvi da se svaki par elemenata skupa  zajedno nalazi u točno jednom od tih podskupova. Dokažite da je tada zajedno nalazi u točno jednom od tih podskupova. Dokažite da je tada  . .
5. Neka su 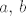 pozitivni realni brojevi takvi da je pozitivni realni brojevi takvi da je 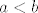 . Definirajmo rekurzivno nizove . Definirajmo rekurzivno nizove 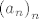 i i 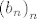 formulama formulama 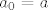 , , 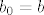 , ,
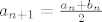 , , 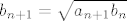 , , 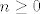 . .
Dokažite da je
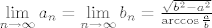 . .
Svaki zadatak je nosio 20 bodova, pisalo se 4 sata.
Evo i rezultata, za ljude koji su prošli.
| Ime | Prezime | Zad1 | Zad2 | Zad3 | Zad4 | Zad5 | Ukupno |
|---|
| Nina | Kamčev | 20 | 2 | 20 | 20 | 0 | 62 | | Petar | Sirković | 20 | 20 | 15 | 3 | 2 | 60 | | Melkior | Ornik | 20 | 15 | 0 | 0 | 1 | 36 | | Ivan | Krijan | 10 | 2 | 19 | 2 | 0 | 33 | | Luka | Rimanić | 10 | 1 | 0 | 0 | 20 | 31 | | Filip | Barl | 10 | 0 | 19 | 0 | 0 | 29 | | Luka | Žunić | 10 | 0 | 15 | 0 | 2 | 27 | | Branimir | Blašković | 1 | 0 | 20 | 3 | 0 | 24 | | Ana | Kontrec | 1 | 2 | 20 | 0 | 1 | 24 | | Nikola | Adžaga | 10 | 3 | 5 | 2 | 2 | 22 | | Petar | Bakić | 0 | 0 | 20 | 2 | 0 | 22 | | Željko | Kereta | 0 | 0 | 20 | 2 | 0 | 22 | | Marko | Božić | 1 | 0 | 20 | 0 | 0 | 21 |
|









