| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
 Postano: 23:31 sub, 16. 10. 2010 Naslov: Primjer 4.9. iz skripte Postano: 23:31 sub, 16. 10. 2010 Naslov: Primjer 4.9. iz skripte |
    |
|
|
rjesavah antikne kolokvije iz vjerojatnosti i tamo naletih na (pod)zadatak oblika:
[latex]\displaystyle \sum_{i=1}^{k} x_i = n; \ k, n \in \mathbb{N}[/latex], samo sto
[latex]\displaystyle \forall x_i, i\in\{1,\dots,k\}, x_i<m, m\in \mathbb{N}[/latex]
sto me (za divno cudo) podsjetilo na primjer 4.9. iz [url=http://web.math.hr/nastava/komb/SKRIPTA.pdf]skripte[/url], samo sto ovdje imamo (jednaku) gornju ogradu na sve [latex]\displaystyle x_i[/latex].
ako je potrebno, zadatak je 3. u [url=http://web.math.hr/nastava/uuv/files/uuv-0708-kol1.pdf]ovom[/url] koloviju, obe grupe.
iskreno, nije mi skroz jasno ni kako se isti primjer rjesava niti sa jednom gornjom ogradom, jer smo se mi vise bazirali na donje ograde, koje radimo supstitucijama jednu po jednu. kako ovdje?
rjesavah antikne kolokvije iz vjerojatnosti i tamo naletih na (pod)zadatak oblika:
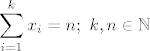 , samo sto , samo sto
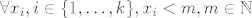
sto me (za divno cudo) podsjetilo na primjer 4.9. iz skripte, samo sto ovdje imamo (jednaku) gornju ogradu na sve 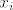 . .
ako je potrebno, zadatak je 3. u ovom koloviju, obe grupe.
iskreno, nije mi skroz jasno ni kako se isti primjer rjesava niti sa jednom gornjom ogradom, jer smo se mi vise bazirali na donje ograde, koje radimo supstitucijama jednu po jednu. kako ovdje?
_________________
...to kaj ona ima kilu viska, ja ne marim...
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:58 sub, 16. 10. 2010 Naslov: Postano: 23:58 sub, 16. 10. 2010 Naslov: |
    |
|
|
Čini mi se najbolje te zadatke riješiti brutalnom silom. :boks:
Na primjer, u zadatku iz prve grupe (zbroj brojeva na 5 kocki je 25) ima ukupno 7 slučajeva: (6, 6, 6, 6, 1), (6, 6, 6, 5, 2), (6, 6, 5, 5, 3), (6, 6, 6, 4, 3), (6, 6, 5, 4, 4), (6, 5, 5, 5, 4) i (5, 5, 5, 5, 5).
Čini mi se najbolje te zadatke riješiti brutalnom silom. 
Na primjer, u zadatku iz prve grupe (zbroj brojeva na 5 kocki je 25) ima ukupno 7 slučajeva: (6, 6, 6, 6, 1), (6, 6, 6, 5, 2), (6, 6, 5, 5, 3), (6, 6, 6, 4, 3), (6, 6, 5, 4, 4), (6, 5, 5, 5, 4) i (5, 5, 5, 5, 5).
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 16:30 ned, 17. 10. 2010 Naslov: Postano: 16:30 ned, 17. 10. 2010 Naslov: |
    |
|
|
Teoretski možeš i bez pogađanja, što bi možda bilo i bolje u nekom složenijem primjeru, ali ovdje samo apsurdno komplicira stvar.
Ukupni broj rješenja jednadžbe x1+x2+x3+x4+x5 = 25, gdje je xi > 0 je (24 povrh 4).
Sada pogledamo slučajeve kada je npr. x1 > 6. Takvih rješenja ima (18 povrh 4). Isto napraviš i za ostalih (5 povrh 1) izbora jedne varijable iz pet.
No tako brojiš viška slučajeve gdje su neke dvije varijable veće od 6, pa trebaš oduzeti (5 povrh 2 izbora dvije varijable iz 5) * (12 povrh 4 rješenja jednadžbe kada su dva iksa veća od 6). Sad si previše puta oduzeo slučajeve kada su tri varijable veće od 6, pa trebaš dodati još (5 povrh 3) * (4 povrh 4) i to je to, dobio si broj rješenja za koje nisu sve varijable <= 6. Kada ga oduzmeš od početnih (24 povrh 4), dobivaš 126 što je točan broj i odgovara broju permutacija onih skupova koje je pmli napisao.
Dakle, pokušavaš izračunati broj rješenje kada nisu svi iksevi manji od 6, a to je kardinalitet unije svih slučajeva kada je jedan od njih veći od 6. No ti slučajevi nisu disjunktni, pa moraš raditi preko FUI. Nije da bih to nazvao elegantnim, ali može se napisati formulom, pa eto :) Možda bi se čak moglo i nekako pojednostaviti, ali moje poznavanje kombinatornih identiteta je preslabo da bih se pokušao upustiti u tako što.
Teoretski možeš i bez pogađanja, što bi možda bilo i bolje u nekom složenijem primjeru, ali ovdje samo apsurdno komplicira stvar.
Ukupni broj rješenja jednadžbe x1+x2+x3+x4+x5 = 25, gdje je xi > 0 je (24 povrh 4).
Sada pogledamo slučajeve kada je npr. x1 > 6. Takvih rješenja ima (18 povrh 4). Isto napraviš i za ostalih (5 povrh 1) izbora jedne varijable iz pet.
No tako brojiš viška slučajeve gdje su neke dvije varijable veće od 6, pa trebaš oduzeti (5 povrh 2 izbora dvije varijable iz 5) * (12 povrh 4 rješenja jednadžbe kada su dva iksa veća od 6). Sad si previše puta oduzeo slučajeve kada su tri varijable veće od 6, pa trebaš dodati još (5 povrh 3) * (4 povrh 4) i to je to, dobio si broj rješenja za koje nisu sve varijable <= 6. Kada ga oduzmeš od početnih (24 povrh 4), dobivaš 126 što je točan broj i odgovara broju permutacija onih skupova koje je pmli napisao.
Dakle, pokušavaš izračunati broj rješenje kada nisu svi iksevi manji od 6, a to je kardinalitet unije svih slučajeva kada je jedan od njih veći od 6. No ti slučajevi nisu disjunktni, pa moraš raditi preko FUI. Nije da bih to nazvao elegantnim, ali može se napisati formulom, pa eto  Možda bi se čak moglo i nekako pojednostaviti, ali moje poznavanje kombinatornih identiteta je preslabo da bih se pokušao upustiti u tako što. Možda bi se čak moglo i nekako pojednostaviti, ali moje poznavanje kombinatornih identiteta je preslabo da bih se pokušao upustiti u tako što.
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 23:22 ned, 17. 10. 2010 Naslov: Postano: 23:22 ned, 17. 10. 2010 Naslov: |
    |
|
|
Ne znam, čitao sam ovo što ste tu pisali i koliko sam skužio treba na 5 kocaka dobiti zbroj 25, jel?
Ako je tako, onda je za svaki od brojeva uvijet i da je >= 1, pa bi kad tražiš broj ukupnih rješenja radio supstituciju za svaki od njih i na kraju dobio jednadžbu x1 + ... + x5 = 25 - 5*1 = 20, xi >= 0. A broj njenih rješenja je [latex]\binom{20+5-1}{5-1} = \binom{24}4[/latex]. Slično onda i kad tražiš broj rješenja kada su npr. dva broja veća od 6, a ostali bilo kakvi (ali strogo veći od nule): od dvaju moraš oduzeti 7, a od ostala tri još uvijek 1, pa na kraju dobivaš jednadžbu y1 + ... + y5 = 25-14-3 = 8, yi >= 0, koja ima onih [latex]\binom{8+5-1}{5-1} = \binom{12}4[/latex] rješenja koja sam spominjao.
Ne znam, čitao sam ovo što ste tu pisali i koliko sam skužio treba na 5 kocaka dobiti zbroj 25, jel?
Ako je tako, onda je za svaki od brojeva uvijet i da je >= 1, pa bi kad tražiš broj ukupnih rješenja radio supstituciju za svaki od njih i na kraju dobio jednadžbu x1 + ... + x5 = 25 - 5*1 = 20, xi >= 0. A broj njenih rješenja je 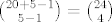 . Slično onda i kad tražiš broj rješenja kada su npr. dva broja veća od 6, a ostali bilo kakvi (ali strogo veći od nule): od dvaju moraš oduzeti 7, a od ostala tri još uvijek 1, pa na kraju dobivaš jednadžbu y1 + ... + y5 = 25-14-3 = 8, yi >= 0, koja ima onih . Slično onda i kad tražiš broj rješenja kada su npr. dva broja veća od 6, a ostali bilo kakvi (ali strogo veći od nule): od dvaju moraš oduzeti 7, a od ostala tri još uvijek 1, pa na kraju dobivaš jednadžbu y1 + ... + y5 = 25-14-3 = 8, yi >= 0, koja ima onih 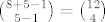 rješenja koja sam spominjao. rješenja koja sam spominjao.
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
|










