|
Prvi... linearnost se trivijalno pokaze (po definiciji). Nadalje, vidi kad je [latex]A + A^\tau = 0[/latex] (to su antisimetricne matrice), pa odatle iskopaj bazu jezgre (baza prostora antisimetricnih matrica) i defekt, a onda imas i sve ostalo. Baza slike jednaka je bazi prostora simetricnih matrica (sto i ima smisla jer se svaka matrica moze prikazati kao suma antisimetricne i simetricne -- to smo radili na Prog 2).
Treci... trazis ortogonalnu projekciju vektora [i]a[/i] na prostor [i]M[/i]. Drugim rijecima, trazis [i]t[/i] takav da je:
[latex]a - tb \in M, \quad b = [1\ 0\ 1\ -1]^\tau[/latex]
jer je [i]M[/i] definiran tako da sadrzi sve i samo one vektore koji su okomiti na [i]b[/i]. Drugim rijecima:
[latex]\langle a - tb, b \rangle = 0[/latex]
Uvrstis:
[latex]0 = [ 2-t\ -1\ -t\ 3+t ] [1\ 0\ 1\ -1]^\tau = 2-t -t -3 -t = -1-3t[/latex]
Dakle,
[latex]t = -1/3[/latex],
pa je trazeni vektor
[latex]\begin{bmatrix} 7/3 \\ -1 \\ 1/3 \\ 8/3\end{bmatrix}[/latex].
P.S. Izgleda mi kao da su vama vektori reci; meni su stupci i mogu se samo nadati da te to nece zbuniti.
Prvi... linearnost se trivijalno pokaze (po definiciji). Nadalje, vidi kad je 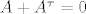 (to su antisimetricne matrice), pa odatle iskopaj bazu jezgre (baza prostora antisimetricnih matrica) i defekt, a onda imas i sve ostalo. Baza slike jednaka je bazi prostora simetricnih matrica (sto i ima smisla jer se svaka matrica moze prikazati kao suma antisimetricne i simetricne – to smo radili na Prog 2). (to su antisimetricne matrice), pa odatle iskopaj bazu jezgre (baza prostora antisimetricnih matrica) i defekt, a onda imas i sve ostalo. Baza slike jednaka je bazi prostora simetricnih matrica (sto i ima smisla jer se svaka matrica moze prikazati kao suma antisimetricne i simetricne – to smo radili na Prog 2).
Treci... trazis ortogonalnu projekciju vektora a na prostor M. Drugim rijecima, trazis t takav da je:
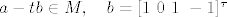
jer je M definiran tako da sadrzi sve i samo one vektore koji su okomiti na b. Drugim rijecima:
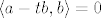
Uvrstis:
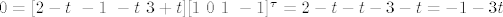
Dakle,
 , ,
pa je trazeni vektor
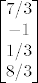 . .
P.S. Izgleda mi kao da su vama vektori reci; meni su stupci i mogu se samo nadati da te to nece zbuniti.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |





