| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 21:44 pon, 3. 10. 2011 Naslov: Dug s demonstratura 3.10. Postano: 21:44 pon, 3. 10. 2011 Naslov: Dug s demonstratura 3.10. |
    |
|
|
Vrijedi li za [latex]A \subset \mathbb{R}^k, B \subset \mathbb{R}^l\qquad\overline{A \times B} = \overline{A} \times \overline{B} \,?[/latex]
Odgovor: da.
Prije samog dokaza, evo male sistematizacije topoloških stvarčica čije ću rezultate koristiti, a možda vam i inače pomogne:
Promatramo neki skup [latex]A \subset \mathbb{R}^n[/latex]. Za svaku točku [latex]x \in \mathbb{R}^n[/latex] vrijedi točno jedno od sljedećeg:
(1) postoji otvorena kugla sa središtem u x koja je cijela sadržana u [latex]A \Leftrightarrow x \in Int A[/latex];
(2) postoji otvorena kugla sa središtem u x koja je cijela sadržana u [latex]A^c \Leftrightarrow x \in Int A^c[/latex];
(3) svaka otvorena kugla sa središtem u x sadrži bar jednu točku iz [latex]A[/latex] i bar jednu točku iz [latex]A^c \Leftrightarrow x \in \partial A[/latex].
[latex]\overline{A}[/latex] je sad (disjunktna!) unija (1) i (3), tj. skup svih točaka iz [latex]\mathbb{R}^n[/latex] t. d. u svakoj kugli oko njih postoji bar jedna točka skupa [latex]A[/latex].
Dakle, skupovi (1), (2) i (3) u disjunktnoj uniji daju cijeli [latex]\mathbb{R}^n[/latex], i ako ih u danoj situaciji odredite, što nije teško kad se malo naviknete na zamišljanje malih kugli, većina muka - nestaje.
Čak se i gomilišta mogu donekle dovesti u vezu s ovim gore: očito su sve točke skupa (1) gomilišta od [latex]A[/latex], sve točke skupa (2) gomilišta od [latex]A^c[/latex], a samo skup (3) je nepredvidiv - njegove točke mogu biti i gomilišta od [latex]A[/latex] i gomilišta od [latex]A^c[/latex] i oboje (ali moraju biti gomilište bar jednog od njih).
A evo sad i dokaza (od ovoga gore koristimo samo tvrdnju: [latex]\overline{A}[/latex] je skup svih točaka iz [latex]\mathbb{R}^n[/latex] t. d. u svakoj kugli oko njih postoji bar jedna točka iz skupa [latex]A[/latex]; kugle gledamo u max-normi (dokaz je tako najjednostavniji)):
Označimo za [latex]x \in \mathbb{R}^{k + l} \_ x = (x^k, x^l)[/latex], gdje [latex]x^k[/latex] označava "podvektor" sastavljen od prvih k, a [latex]x^l[/latex] od sljedećih l koordinata vektora x. Sad vrijedi:
[latex]x = (x^k, x^l) \in \overline{A \times B}[/latex]
[latex]\qquad \Leftrightarrow \forall \epsilon > 0 \quad \exists y = (y^k, y^l) \in A \times B \qquad \mathrm{t. d.} \qquad \|y - x\|_{\infty} < \epsilon[/latex]
(y je ona točka koja postoji u kugli [latex]K_\infty (x, \epsilon)[/latex])
[latex]\Leftrightarrow \forall \epsilon > 0 \quad \exists y^k \in A \_\mathrm{i}\_ y^l \in B \quad \mathrm{t. d.} \quad \|y^k - x^k\|_{\infty} < \epsilon \quad \mathrm{i} \quad\|y^l - x^l\|_{\infty} < \epsilon[/latex]
(ovdje smo samo koristili da je [latex](y^k, y^l) \in A \times B \Leftrightarrow y^k \in A \_ \mathrm{i} \_ y^l \in B[/latex] te da je maksimum [latex]|y_i - x_i|, i = 1, ..., k + l[/latex] manji od [latex]\epsilon[/latex] za sve [latex]i[/latex]-eve akko to vrijedi i za prvih k i za sljedećih l [latex]i[/latex]-eva)
[latex]\Leftrightarrow x^k \in \overline{A}\_ \mathrm{i}^\_x^l \in \overline{B}[/latex]
[latex]\Leftrightarrow (x^k, x^l) \in \overline{A}\times\overline{B}[/latex]
Postoje i drugi načini da se ovo dokaže. Npr., kad se malo ufurate u nizove i limese, moći ćete ovo dokazati pomoću njih. Hint: [latex]\overline{A}[/latex] je skup svih mogućih limesa nizova u [latex]A[/latex] koji konvergiraju u [latex]\mathbb{R}^n[/latex].
Vrijedi li za 
Odgovor: da.
Prije samog dokaza, evo male sistematizacije topoloških stvarčica čije ću rezultate koristiti, a možda vam i inače pomogne:
Promatramo neki skup 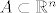 . Za svaku točku . Za svaku točku  vrijedi točno jedno od sljedećeg: vrijedi točno jedno od sljedećeg:
(1) postoji otvorena kugla sa središtem u x koja je cijela sadržana u 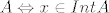 ; ;
(2) postoji otvorena kugla sa središtem u x koja je cijela sadržana u 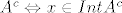 ; ;
(3) svaka otvorena kugla sa središtem u x sadrži bar jednu točku iz  i bar jednu točku iz i bar jednu točku iz 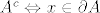 . .
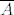 je sad (disjunktna!) unija (1) i (3), tj. skup svih točaka iz je sad (disjunktna!) unija (1) i (3), tj. skup svih točaka iz  t. d. u svakoj kugli oko njih postoji bar jedna točka skupa t. d. u svakoj kugli oko njih postoji bar jedna točka skupa  . .
Dakle, skupovi (1), (2) i (3) u disjunktnoj uniji daju cijeli  , i ako ih u danoj situaciji odredite, što nije teško kad se malo naviknete na zamišljanje malih kugli, većina muka - nestaje. , i ako ih u danoj situaciji odredite, što nije teško kad se malo naviknete na zamišljanje malih kugli, većina muka - nestaje.
Čak se i gomilišta mogu donekle dovesti u vezu s ovim gore: očito su sve točke skupa (1) gomilišta od  , sve točke skupa (2) gomilišta od , sve točke skupa (2) gomilišta od 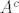 , a samo skup (3) je nepredvidiv - njegove točke mogu biti i gomilišta od , a samo skup (3) je nepredvidiv - njegove točke mogu biti i gomilišta od  i gomilišta od i gomilišta od 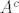 i oboje (ali moraju biti gomilište bar jednog od njih). i oboje (ali moraju biti gomilište bar jednog od njih).
A evo sad i dokaza (od ovoga gore koristimo samo tvrdnju: 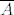 je skup svih točaka iz je skup svih točaka iz  t. d. u svakoj kugli oko njih postoji bar jedna točka iz skupa t. d. u svakoj kugli oko njih postoji bar jedna točka iz skupa  ; kugle gledamo u max-normi (dokaz je tako najjednostavniji)): ; kugle gledamo u max-normi (dokaz je tako najjednostavniji)):
Označimo za 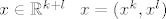 , gdje , gdje 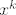 označava "podvektor" sastavljen od prvih k, a označava "podvektor" sastavljen od prvih k, a 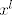 od sljedećih l koordinata vektora x. Sad vrijedi: od sljedećih l koordinata vektora x. Sad vrijedi:
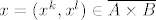
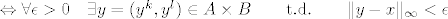
(y je ona točka koja postoji u kugli 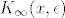 ) )
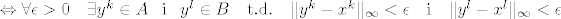
(ovdje smo samo koristili da je 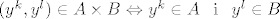 te da je maksimum te da je maksimum 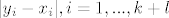 manji od manji od  za sve za sve  -eve akko to vrijedi i za prvih k i za sljedećih l -eve akko to vrijedi i za prvih k i za sljedećih l  -eva) -eva)
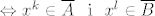
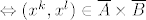
Postoje i drugi načini da se ovo dokaže. Npr., kad se malo ufurate u nizove i limese, moći ćete ovo dokazati pomoću njih. Hint: 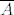 je skup svih mogućih limesa nizova u je skup svih mogućih limesa nizova u  koji konvergiraju u koji konvergiraju u  . .
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 19:57 ned, 4. 12. 2011 Naslov: Postano: 19:57 ned, 4. 12. 2011 Naslov: |
    |
|
|
Demonstrature su svaki tjedan u redovitim terminima, ali samo ako se netko najavi Ani mailom (inače se najvjerojatnije neće pojaviti). Da se sad ne zamaraš, ja ću joj reći da sutra svakako bude tamo.
Istina, malo je nezgodno što demonstrature nisu u jednom terminu, ali prilikom određivanja u rasporedu jednostavno nije postojao jedinstveni termin koji bi odgovarao objema grupama i Aninu rasporedu :( , pa ćete se morati snaći ovako...
Demonstrature su svaki tjedan u redovitim terminima, ali samo ako se netko najavi Ani mailom (inače se najvjerojatnije neće pojaviti). Da se sad ne zamaraš, ja ću joj reći da sutra svakako bude tamo.
Istina, malo je nezgodno što demonstrature nisu u jednom terminu, ali prilikom određivanja u rasporedu jednostavno nije postojao jedinstveni termin koji bi odgovarao objema grupama i Aninu rasporedu  , pa ćete se morati snaći ovako... , pa ćete se morati snaći ovako...
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 11:30 čet, 22. 12. 2011 Naslov: Dug s demonstratura 21.12. Postano: 11:30 čet, 22. 12. 2011 Naslov: Dug s demonstratura 21.12. |
    |
|
|
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
3. (b) (na demonstraturama je dana malo kriva uputa pa evo ispravka:)
Očito, trebamo maksimizirati fju [tex]V(x,y,z)=xyz[/tex] na skupu [tex]xy+xz+yz=27[/tex] (naravno, zanimaju nas samo točke sa x, y, z >0).
E sad, ima više načina kako krenuti:
1. klasični uvjetni ekstremi:
[dtex](yz,xz,xy)=\lambda (y+z,x+z,x+y)[/dtex]
[dtex]\frac{y+z}{yz}=\frac{x+z}{xz}=\frac{x+y}{xy}(=\frac{1}{\lambda})[/dtex]
[dtex]\frac{1}{z}+\frac{1}{y}=\frac{1}{z}+\frac{1}{x}=\frac{1}{y}+\frac{1}{x}[/dtex]
odakle se lako vidi da mora biti x=y=z=3.
Dakle, jedini kandidat za globalni maksimum nam je (3, 3, 3) (za x, y, z > 0).
2. Nećemo uvjetne ekstreme: maksimiziramo fju
[dtex]V(x,y)=xy\frac{27-xy}{x+y}[/dtex]
Tražimo stacionarne točke, opet nas zanima samo (3, 3, 3), pomoću Hessea sad možemo i provjeriti da se radi o lokalnom maksimumu.
Ali u oba načina još nismo pokazali da se radi o globalnom maksimumu, to se može npr. uz malo petljanja sa sredinama:
pretp. da je za neku (y, z) [tex]V(y, z) > 27 = V(3, 3)[/tex].
[dtex]\frac{27-yz}{y+z}yz>27[/dtex]
[dtex]27yz>y^2z^2+27y+27z\stackrel{A-G}{\geq}3\sqrt[3]{(y^2z^2)(27y)(27z)}=27yz[/dtex]
Kontradikcija!
Dakle, stvarno se radi o globalnom maksimumu.
3. Može vam pasti na pamet da malo promijenite slova i drastično pojednostavite zadatak:
uočimo da je za x, y, z > 0 točka (x, y, z) jedinstveno određena ako znamo (xy, xz, yz). Pa uvedimo nova slova:
[dtex]a:=xy, b:= xz, c:= yz[/dtex]
Uz uvjet a+b+c=27 pokušavamo maksimizirati fju
[dtex]V(a,b,c)=\sqrt{abc}[/dtex]
Maknimo prvo korijen i maksimizirajmo radije
[dtex]f(a,b,c)=abc[/dtex]
Sad možemo dalje kao i na prva dva načina, a možemo i samo iskoristiti sredine:
[dtex]abc\stackrel{G-A}{\leq}(\frac{a+b+c}{3})^3=(\frac{27}{3})^3=3^6[/dtex]
a jednakost vrijedi akko a = b = c (= 9), tj. x = y = z = 3.
I zadatak riješen!
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
3. (b) (na demonstraturama je dana malo kriva uputa pa evo ispravka:)
Očito, trebamo maksimizirati fju [tex]V(x,y,z)=xyz[/tex] na skupu [tex]xy+xz+yz=27[/tex] (naravno, zanimaju nas samo točke sa x, y, z >0).
E sad, ima više načina kako krenuti:
1. klasični uvjetni ekstremi:
[dtex](yz,xz,xy)=\lambda (y+z,x+z,x+y)[/dtex]
[dtex]\frac{y+z}{yz}=\frac{x+z}{xz}=\frac{x+y}{xy}(=\frac{1}{\lambda})[/dtex]
[dtex]\frac{1}{z}+\frac{1}{y}=\frac{1}{z}+\frac{1}{x}=\frac{1}{y}+\frac{1}{x}[/dtex]
odakle se lako vidi da mora biti x=y=z=3.
Dakle, jedini kandidat za globalni maksimum nam je (3, 3, 3) (za x, y, z > 0).
2. Nećemo uvjetne ekstreme: maksimiziramo fju
[dtex]V(x,y)=xy\frac{27-xy}{x+y}[/dtex]
Tražimo stacionarne točke, opet nas zanima samo (3, 3, 3), pomoću Hessea sad možemo i provjeriti da se radi o lokalnom maksimumu.
Ali u oba načina još nismo pokazali da se radi o globalnom maksimumu, to se može npr. uz malo petljanja sa sredinama:
pretp. da je za neku (y, z) [tex]V(y, z) > 27 = V(3, 3)[/tex].
[dtex]\frac{27-yz}{y+z}yz>27[/dtex]
[dtex]27yz>y^2z^2+27y+27z\stackrel{A-G}{\geq}3\sqrt[3]{(y^2z^2)(27y)(27z)}=27yz[/dtex]
Kontradikcija!
Dakle, stvarno se radi o globalnom maksimumu.
3. Može vam pasti na pamet da malo promijenite slova i drastično pojednostavite zadatak:
uočimo da je za x, y, z > 0 točka (x, y, z) jedinstveno određena ako znamo (xy, xz, yz). Pa uvedimo nova slova:
[dtex]a:=xy, b:= xz, c:= yz[/dtex]
Uz uvjet a+b+c=27 pokušavamo maksimizirati fju
[dtex]V(a,b,c)=\sqrt{abc}[/dtex]
Maknimo prvo korijen i maksimizirajmo radije
[dtex]f(a,b,c)=abc[/dtex]
Sad možemo dalje kao i na prva dva načina, a možemo i samo iskoristiti sredine:
[dtex]abc\stackrel{G-A}{\leq}(\frac{a+b+c}{3})^3=(\frac{27}{3})^3=3^6[/dtex]
a jednakost vrijedi akko a = b = c (= 9), tj. x = y = z = 3.
I zadatak riješen!
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
fejky
Forumaš(ica)
Pridružen/a: 23. 06. 2010. (16:53:45)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
|






