| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
Goran Muic
Forumaš(ica)
Pridružen/a: 12. 06. 2006. (09:18:23)
Postovi: (71)16
|
|
| [Vrh] |
|
rom
Forumaš(ica)
Pridružen/a: 26. 10. 2010. (11:10:35)
Postovi: (2D)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 13:16 pet, 7. 10. 2011 Naslov: Postano: 13:16 pet, 7. 10. 2011 Naslov: |
    |
|
|
Zapravo su dosta slicna ta 2 zadatka:
2.9:
Neka je x iz V takav da ga ponistavaju svi funkcionali iz V'.
Zadajmo bazu za V: [latex](e_1,\dots,e_n)[/latex] i nadjimo njoj dualnu bazu za V', [latex](f_1,\dots,f_n)[/latex]. Sada x raspisemo po vektorima nase baze:
[latex]\displaystyle x=\sum_{i=1}^n \alpha_ie_i[/latex]
Sada gledamo kako [latex]f_j[/latex] djeluje na x, za j=1,..., n
[latex]\displaystyle 0=f_j(x)=\sum_{i=1}^n \alpha_if_j(e_i) = \alpha_j[/latex]
pritom prva jednakost vrijedi jer svaki funkcional slika x u 0, druga vrijedi zbog linearnosti, a 3. je iz svojstva dualne baze: [latex] f_j(e_i)=\delta_{ij}[/latex]
iz ovoga se vidi da su svi koeficijenti alfa=0, pa je i x=0.
2.8
Slijedi iz 2.9:
Neka je [latex]x \in \bigcap_{i=1}^n ker f_i[/latex]
To znaci da svaki funkcional iz baze slika x u 0, ali iz toga direktno zakljucujemo da isto vrijedi za sve funkcionale iz V' (jer se svaki funkcional moze prikazati kao linearna kombinacija funkcionala iz baze).
Sada se zadatak svodi na 2.9 - x ponistavaju svi funkcionali, pa mora biti x=0.
Zapravo su dosta slicna ta 2 zadatka:
2.9:
Neka je x iz V takav da ga ponistavaju svi funkcionali iz V'.
Zadajmo bazu za V:  i nadjimo njoj dualnu bazu za V', i nadjimo njoj dualnu bazu za V',  . Sada x raspisemo po vektorima nase baze: . Sada x raspisemo po vektorima nase baze:
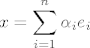
Sada gledamo kako 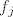 djeluje na x, za j=1,..., n djeluje na x, za j=1,..., n
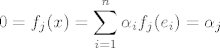
pritom prva jednakost vrijedi jer svaki funkcional slika x u 0, druga vrijedi zbog linearnosti, a 3. je iz svojstva dualne baze: 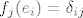
iz ovoga se vidi da su svi koeficijenti alfa=0, pa je i x=0.
2.8
Slijedi iz 2.9:
Neka je 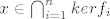
To znaci da svaki funkcional iz baze slika x u 0, ali iz toga direktno zakljucujemo da isto vrijedi za sve funkcionale iz V' (jer se svaki funkcional moze prikazati kao linearna kombinacija funkcionala iz baze).
Sada se zadatak svodi na 2.9 - x ponistavaju svi funkcionali, pa mora biti x=0.
|
|
| [Vrh] |
|
rom
Forumaš(ica)
Pridružen/a: 26. 10. 2010. (11:10:35)
Postovi: (2D)16
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)

Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol: 
Lokacija: pod stolom
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
maxi
Gost
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
|








