| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
lavicha
Forumaš(ica)
Pridružen/a: 15. 10. 2010. (18:25:49)
Postovi: (1A)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 16:46 ned, 20. 2. 2011 Naslov: Postano: 16:46 ned, 20. 2. 2011 Naslov: |
    |
|
|
[url=http://www.wolframalpha.com/]WolframAlpha[/url] ti je uvijek na raspolaganju. Za deriviranje imaš funkciju D, koja ima ovaj oblik:
[code:1]D[f(x), x][/code:1]
Prvo se piše funkcija koju želiš derivirati, a zatim po čemu se derivira. Ako želiš odrediti n-tu derivaciju (n je neki odabrani broj, rijetko će ti dati općenito rješenje), pišeš:
[code:1]D[f(x), {x, n}][/code:1]
Čak imaš i opciju Show steps.
Ako naiđeš na neke zadatke koje WolframAlpha ne može rješiti, slobodno pitaj. :)
WolframAlpha ti je uvijek na raspolaganju. Za deriviranje imaš funkciju D, koja ima ovaj oblik:
Prvo se piše funkcija koju želiš derivirati, a zatim po čemu se derivira. Ako želiš odrediti n-tu derivaciju (n je neki odabrani broj, rijetko će ti dati općenito rješenje), pišeš:
Čak imaš i opciju Show steps.
Ako naiđeš na neke zadatke koje WolframAlpha ne može rješiti, slobodno pitaj. 
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:50 uto, 22. 2. 2011 Naslov: Postano: 21:50 uto, 22. 2. 2011 Naslov: |
    |
|
|
Ha dobro, ne znam jesi li ti i sama probala, pa neću ulaziti u detalje, da ne pokvarim veselje. :)
Dakle, u ovom prvom, deriviraj obje strane: po formuli o derivaciji kompozicija dobivaš [latex]e^{f(x)}f'(x)+x^2f'(x)+2xf(x)+e^{-x}=0[/latex], ako sam ja to dobro i mudro izračunao. Specijalno, sad možeš to srediti da prikažeš baš [latex]f'(x)[/latex]. Ako dobro napamet računam, [latex]f'(x)=-\displaystyle\frac{e^{-x}+2xf(x)}{e^{f(x)}+x^2}[/latex]. Sad možeš i iz toga (ili ovog izraza gore) prikazati i [latex]f''[/latex] pomoću [latex]f[/latex] (zapravo, prikazat ćemo [latex]f''[/latex] pomoću [latex]f[/latex] i [latex]f'[/latex], a budući da znamo prikazati [latex]f'[/latex] pomoću [latex]f[/latex], sposobni smo prikazati drugu derivaciju samo pomoću [latex]f[/latex]. No, iz razloga personalnog osjećaja besmisla, neću to učiniti. :)).
Ako ja gore dobro računam, imamo [latex]e^{f(x)}f''(x)+e^{f(x)}(f'(x))^2+x^2f''(x)+2xf'(x)+2xf'(x)+2f(x)-e^{-x}=0[/latex]. (Moguće da sam tu učinio sad neku bezveze grešku, ali ajde, nema veze. :D) E, i sad je to to: opet bismo mogli [latex]f''(x)[/latex] izvući na drugu stranu i prikazati pomoću ostalih, kao za [latex]f'[/latex], ali taj dio prepuštam tebi.
Što se [latex]f'(0)[/latex] i [latex]f''(0)[/latex] tiče, uvrstimo [latex]x=0[/latex] u dvije jednadžbe koje smo gore dobili (jedna ova za prvu, a druga za drugu derivaciju). Dobivamo [latex]e^{f(0)}f'(0)+0^2f'(0)+2\cdot0f(0)+e^{-0}=0[/latex], tj. [latex]f'(0)=-\displaystyle\frac{1}{e^{f(0)}}[/latex]. Budući da je [latex]f(0)=0[/latex], što dobivaš uvrštavanjem [latex]x=0[/latex] u originalni uvjet zadatka, imamo [latex]f'(0)=-1[/latex]. Za drugu derivaciju dobivamo iz druge jednadžbe [latex]f''(0)+1-1=0[/latex], ako sam dobro izračunao, tj. [latex]f''(0)=0[/latex].
Eto, kažem, sad sam ovo na brzinu računao, tako da sam vjerojatno negdje pogriješio, ali ovo je koncept.
Što se tiče drugog zadatka, tu ću više ostaviti tebi. :) Prvo, primijeti (i dokaži) da je [latex]f[/latex] zbroj strogo rastućih funkcija. Dakle, i sama je strogo rastuća, pa je injekcija. Drugo, f(2)=10+e^8, pa je očito [latex]10+e^8[/latex] u slici funkcije. Time sad i po formuli za derivaciju inverza dobivamo i da je valjda [latex](f^{-1})'(10+e^8)=\displaystyle\frac{1}{f'(2)}=\displaystyle\frac{1}{13+12e^8}[/latex]. Ponovno, ako sam ja to sad dobro napamet izračunao... sorry ako nisam. :oops:
Eto, još jednom, pitaj ako ti se nešto čini krivo ili ako bude problema pri formalnom rješavanju. :)
Ha dobro, ne znam jesi li ti i sama probala, pa neću ulaziti u detalje, da ne pokvarim veselje. 
Dakle, u ovom prvom, deriviraj obje strane: po formuli o derivaciji kompozicija dobivaš  , ako sam ja to dobro i mudro izračunao. Specijalno, sad možeš to srediti da prikažeš baš , ako sam ja to dobro i mudro izračunao. Specijalno, sad možeš to srediti da prikažeš baš  . Ako dobro napamet računam, . Ako dobro napamet računam,  . Sad možeš i iz toga (ili ovog izraza gore) prikazati i . Sad možeš i iz toga (ili ovog izraza gore) prikazati i  pomoću pomoću  (zapravo, prikazat ćemo (zapravo, prikazat ćemo  pomoću pomoću  i i 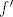 , a budući da znamo prikazati , a budući da znamo prikazati 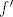 pomoću pomoću  , sposobni smo prikazati drugu derivaciju samo pomoću , sposobni smo prikazati drugu derivaciju samo pomoću  . No, iz razloga personalnog osjećaja besmisla, neću to učiniti. . No, iz razloga personalnog osjećaja besmisla, neću to učiniti.  ). ).
Ako ja gore dobro računam, imamo 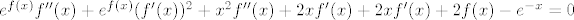 . (Moguće da sam tu učinio sad neku bezveze grešku, ali ajde, nema veze. . (Moguće da sam tu učinio sad neku bezveze grešku, ali ajde, nema veze.  ) E, i sad je to to: opet bismo mogli ) E, i sad je to to: opet bismo mogli 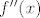 izvući na drugu stranu i prikazati pomoću ostalih, kao za izvući na drugu stranu i prikazati pomoću ostalih, kao za 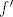 , ali taj dio prepuštam tebi. , ali taj dio prepuštam tebi.
Što se 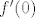 i i 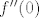 tiče, uvrstimo tiče, uvrstimo  u dvije jednadžbe koje smo gore dobili (jedna ova za prvu, a druga za drugu derivaciju). Dobivamo u dvije jednadžbe koje smo gore dobili (jedna ova za prvu, a druga za drugu derivaciju). Dobivamo 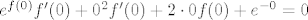 , tj. , tj.  . Budući da je . Budući da je  , što dobivaš uvrštavanjem , što dobivaš uvrštavanjem  u originalni uvjet zadatka, imamo u originalni uvjet zadatka, imamo 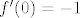 . Za drugu derivaciju dobivamo iz druge jednadžbe . Za drugu derivaciju dobivamo iz druge jednadžbe 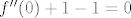 , ako sam dobro izračunao, tj. , ako sam dobro izračunao, tj. 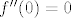 . .
Eto, kažem, sad sam ovo na brzinu računao, tako da sam vjerojatno negdje pogriješio, ali ovo je koncept.
Što se tiče drugog zadatka, tu ću više ostaviti tebi.  Prvo, primijeti (i dokaži) da je Prvo, primijeti (i dokaži) da je  zbroj strogo rastućih funkcija. Dakle, i sama je strogo rastuća, pa je injekcija. Drugo, f(2)=10+e^8, pa je očito zbroj strogo rastućih funkcija. Dakle, i sama je strogo rastuća, pa je injekcija. Drugo, f(2)=10+e^8, pa je očito 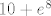 u slici funkcije. Time sad i po formuli za derivaciju inverza dobivamo i da je valjda u slici funkcije. Time sad i po formuli za derivaciju inverza dobivamo i da je valjda 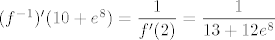 . Ponovno, ako sam ja to sad dobro napamet izračunao... sorry ako nisam. . Ponovno, ako sam ja to sad dobro napamet izračunao... sorry ako nisam. 
Eto, još jednom, pitaj ako ti se nešto čini krivo ili ako bude problema pri formalnom rješavanju. 
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
 Postano: 20:16 sub, 26. 2. 2011 Naslov: Postano: 20:16 sub, 26. 2. 2011 Naslov: |
    |
|
|
[quote="mornik"]Ha dobro, ne znam jesi li ti i sama probala, pa neću ulaziti u detalje, da ne pokvarim veselje. :)
Dakle, u ovom prvom, deriviraj obje strane: po formuli o derivaciji kompozicija dobivaš [latex]e^{f(x)}f'(x)+x^2f'(x)+2xf(x)+e^{-x}=0[/latex], ako sam ja to dobro i mudro izračunao. Specijalno, sad možeš to srediti da prikažeš baš [latex]f'(x)[/latex]. Ako dobro napamet računam, [latex]f'(x)=-\displaystyle\frac{e^{-x}+2xf(x)}{e^{f(x)}+x^2}[/latex]. Sad možeš i iz toga (ili ovog izraza gore) prikazati i [latex]f''[/latex] pomoću [latex]f[/latex] (zapravo, prikazat ćemo [latex]f''[/latex] pomoću [latex]f[/latex] i [latex]f'[/latex], a budući da znamo prikazati [latex]f'[/latex] pomoću [latex]f[/latex], sposobni smo prikazati drugu derivaciju samo pomoću [latex]f[/latex]. No, iz razloga personalnog osjećaja besmisla, neću to učiniti. :)).
Ako ja gore dobro računam, imamo [latex]e^{f(x)}f''(x)+e^{f(x)}(f'(x))^2+x^2f''(x)+2xf'(x)+2xf'(x)+2f(x)-e^{-x}=0[/latex]. (Moguće da sam tu učinio sad neku bezveze grešku, ali ajde, nema veze. :D) E, i sad je to to: opet bismo mogli [latex]f''(x)[/latex] izvući na drugu stranu i prikazati pomoću ostalih, kao za [latex]f'[/latex], ali taj dio prepuštam tebi.
Što se [latex]f'(0)[/latex] i [latex]f''(0)[/latex] tiče, uvrstimo [latex]x=0[/latex] u dvije jednadžbe koje smo gore dobili (jedna ova za prvu, a druga za drugu derivaciju). Dobivamo [latex]e^{f(0)}f'(0)+0^2f'(0)+2\cdot0f(0)+e^{-0}=0[/latex], tj. [latex]f'(0)=-\displaystyle\frac{1}{e^{f(0)}}[/latex]. Budući da je [latex]f(0)=0[/latex], što dobivaš uvrštavanjem [latex]x=0[/latex] u originalni uvjet zadatka, imamo [latex]f'(0)=-1[/latex]. Za drugu derivaciju dobivamo iz druge jednadžbe [latex]f''(0)+1-1=0[/latex], ako sam dobro izračunao, tj. [latex]f''(0)=0[/latex].
Eto, kažem, sad sam ovo na brzinu računao, tako da sam vjerojatno negdje pogriješio, ali ovo je koncept.
Što se tiče drugog zadatka, tu ću više ostaviti tebi. :) Prvo, primijeti (i dokaži) da je [latex]f[/latex] zbroj strogo rastućih funkcija. Dakle, i sama je strogo rastuća, pa je injekcija. Drugo, f(2)=10+e^8, pa je očito [latex]10+e^8[/latex] u slici funkcije. Time sad i po formuli za derivaciju inverza dobivamo i da je valjda [latex](f^{-1})'(10+e^8)=\displaystyle\frac{1}{f'(2)}=\displaystyle\frac{1}{13+12e^8}[/latex]. Ponovno, ako sam ja to sad dobro napamet izračunao... sorry ako nisam. :oops:
Eto, još jednom, pitaj ako ti se nešto čini krivo ili ako bude problema pri formalnom rješavanju. :)[/quote]
sve jasno i nigdje nisi grešku napravioo. hvala ti puno na pomoći :D
| mornik (napisa): | Ha dobro, ne znam jesi li ti i sama probala, pa neću ulaziti u detalje, da ne pokvarim veselje. 
Dakle, u ovom prvom, deriviraj obje strane: po formuli o derivaciji kompozicija dobivaš  , ako sam ja to dobro i mudro izračunao. Specijalno, sad možeš to srediti da prikažeš baš , ako sam ja to dobro i mudro izračunao. Specijalno, sad možeš to srediti da prikažeš baš  . Ako dobro napamet računam, . Ako dobro napamet računam,  . Sad možeš i iz toga (ili ovog izraza gore) prikazati i . Sad možeš i iz toga (ili ovog izraza gore) prikazati i  pomoću pomoću  (zapravo, prikazat ćemo (zapravo, prikazat ćemo  pomoću pomoću  i i 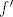 , a budući da znamo prikazati , a budući da znamo prikazati 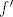 pomoću pomoću  , sposobni smo prikazati drugu derivaciju samo pomoću , sposobni smo prikazati drugu derivaciju samo pomoću  . No, iz razloga personalnog osjećaja besmisla, neću to učiniti. . No, iz razloga personalnog osjećaja besmisla, neću to učiniti.  ). ).
Ako ja gore dobro računam, imamo 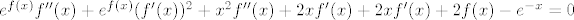 . (Moguće da sam tu učinio sad neku bezveze grešku, ali ajde, nema veze. . (Moguće da sam tu učinio sad neku bezveze grešku, ali ajde, nema veze.  ) E, i sad je to to: opet bismo mogli ) E, i sad je to to: opet bismo mogli 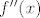 izvući na drugu stranu i prikazati pomoću ostalih, kao za izvući na drugu stranu i prikazati pomoću ostalih, kao za 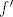 , ali taj dio prepuštam tebi. , ali taj dio prepuštam tebi.
Što se 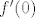 i i 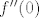 tiče, uvrstimo tiče, uvrstimo  u dvije jednadžbe koje smo gore dobili (jedna ova za prvu, a druga za drugu derivaciju). Dobivamo u dvije jednadžbe koje smo gore dobili (jedna ova za prvu, a druga za drugu derivaciju). Dobivamo 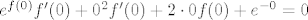 , tj. , tj.  . Budući da je . Budući da je  , što dobivaš uvrštavanjem , što dobivaš uvrštavanjem  u originalni uvjet zadatka, imamo u originalni uvjet zadatka, imamo 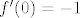 . Za drugu derivaciju dobivamo iz druge jednadžbe . Za drugu derivaciju dobivamo iz druge jednadžbe 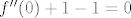 , ako sam dobro izračunao, tj. , ako sam dobro izračunao, tj. 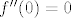 . .
Eto, kažem, sad sam ovo na brzinu računao, tako da sam vjerojatno negdje pogriješio, ali ovo je koncept.
Što se tiče drugog zadatka, tu ću više ostaviti tebi.  Prvo, primijeti (i dokaži) da je Prvo, primijeti (i dokaži) da je  zbroj strogo rastućih funkcija. Dakle, i sama je strogo rastuća, pa je injekcija. Drugo, f(2)=10+e^8, pa je očito zbroj strogo rastućih funkcija. Dakle, i sama je strogo rastuća, pa je injekcija. Drugo, f(2)=10+e^8, pa je očito 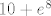 u slici funkcije. Time sad i po formuli za derivaciju inverza dobivamo i da je valjda u slici funkcije. Time sad i po formuli za derivaciju inverza dobivamo i da je valjda 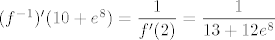 . Ponovno, ako sam ja to sad dobro napamet izračunao... sorry ako nisam. . Ponovno, ako sam ja to sad dobro napamet izračunao... sorry ako nisam. 
Eto, još jednom, pitaj ako ti se nešto čini krivo ili ako bude problema pri formalnom rješavanju.  |
sve jasno i nigdje nisi grešku napravioo. hvala ti puno na pomoći 
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
Vanja_
Forumaš(ica)

Pridružen/a: 21. 11. 2009. (14:38:39)
Postovi: (2C)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 20:22 čet, 3. 3. 2011 Naslov: Postano: 20:22 čet, 3. 3. 2011 Naslov: |
    |
|
|
Nisam baš u potpunosti shvatio kako ide tvoje rješenje :), ali ideja (barem sigurno za prvu/treću grupu, pretpostavljam da si o njima govorio) jest tu - svesti stotu derivaciju na 98. derivaciju, pa nju na 96. itd. Tako nešto nije teško izvesti, samo idemo običnim Leibnizovim pravilom. Mislim da to zapravo i jest ovo što si ti htio izvesti, samo trebaš dovući do kraja.
Rješavam recimo prvu grupu, s [latex]\sin(x^2)[/latex]. Neka je to [latex]f(x)[/latex]. Sad, želimo dobiti [latex]f^{(100)}(0)[/latex]. Dobro, prvo derivirajmo [latex]f[/latex] jednom. Dobivamo da je [latex]f'(x)=2x\cos(x^2)[/latex]. OK, sad to derivirajmo [latex]99[/latex] puta - po Leibnizu (uz uvrštavanje [latex]x=0[/latex] gdje možemo) dobivamo da je [latex]f^{(100)}(x)=2\cdot 99(\cos(x^2))^{(98)}[/latex]. E, a sad samo izvedemo za kosinus isto što smo i za sinus: [latex](\cos(x^2))^{(98)}=(-2x\sin(x^2))^{(97)}[/latex]. Po Leibnizu, to iznosi [latex]-2\cdot 97\cdot \sin(x^2)^{(96)}[/latex] u nuli. E, a sad si, zapravo, obzirom na to da isti postupak gore možemo proizvesti počevši od proizvoljnog [latex]n\geq 4[/latex], a ne od [latex]100[/latex] dobio rekurziju koju si htio: [latex]f^{(n)}(0)= -4\cdot (n-1)\cdot (n-3)f^{(n-4)}(0)[/latex]. Na taj način direktno dolaziš na ono što smo htjeli: [latex]f^{(100)}(0)=(-1)^{25}\cdot 99!!\cdot \sin (0^2)=0[/latex].
Evo, nadam se da je to OK, možda sam pogriješio u nekom graničnom slučaju ili nešto, ali to je generalno ideja. :) Treći zadatak (tj. treća grupa) je isti (dapače, usput smo i njega manje-više riješili :D), a pretpostavljam da se i drugi i četvrti svode na manje-više to... reci ako ipak ne. :)
Nisam baš u potpunosti shvatio kako ide tvoje rješenje  , ali ideja (barem sigurno za prvu/treću grupu, pretpostavljam da si o njima govorio) jest tu - svesti stotu derivaciju na 98. derivaciju, pa nju na 96. itd. Tako nešto nije teško izvesti, samo idemo običnim Leibnizovim pravilom. Mislim da to zapravo i jest ovo što si ti htio izvesti, samo trebaš dovući do kraja. , ali ideja (barem sigurno za prvu/treću grupu, pretpostavljam da si o njima govorio) jest tu - svesti stotu derivaciju na 98. derivaciju, pa nju na 96. itd. Tako nešto nije teško izvesti, samo idemo običnim Leibnizovim pravilom. Mislim da to zapravo i jest ovo što si ti htio izvesti, samo trebaš dovući do kraja.
Rješavam recimo prvu grupu, s 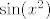 . Neka je to . Neka je to 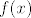 . Sad, želimo dobiti . Sad, želimo dobiti 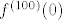 . Dobro, prvo derivirajmo . Dobro, prvo derivirajmo  jednom. Dobivamo da je jednom. Dobivamo da je 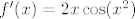 . OK, sad to derivirajmo . OK, sad to derivirajmo 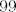 puta - po Leibnizu (uz uvrštavanje puta - po Leibnizu (uz uvrštavanje  gdje možemo) dobivamo da je gdje možemo) dobivamo da je  . E, a sad samo izvedemo za kosinus isto što smo i za sinus: . E, a sad samo izvedemo za kosinus isto što smo i za sinus: 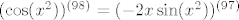 . Po Leibnizu, to iznosi . Po Leibnizu, to iznosi  u nuli. E, a sad si, zapravo, obzirom na to da isti postupak gore možemo proizvesti počevši od proizvoljnog u nuli. E, a sad si, zapravo, obzirom na to da isti postupak gore možemo proizvesti počevši od proizvoljnog 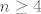 , a ne od , a ne od 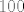 dobio rekurziju koju si htio: dobio rekurziju koju si htio: 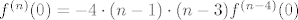 . Na taj način direktno dolaziš na ono što smo htjeli: . Na taj način direktno dolaziš na ono što smo htjeli: 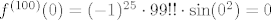 . .
Evo, nadam se da je to OK, možda sam pogriješio u nekom graničnom slučaju ili nešto, ali to je generalno ideja.  Treći zadatak (tj. treća grupa) je isti (dapače, usput smo i njega manje-više riješili Treći zadatak (tj. treća grupa) je isti (dapače, usput smo i njega manje-više riješili  ), a pretpostavljam da se i drugi i četvrti svode na manje-više to... reci ako ipak ne. ), a pretpostavljam da se i drugi i četvrti svode na manje-više to... reci ako ipak ne. 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:35 čet, 3. 3. 2011 Naslov: Postano: 20:35 čet, 3. 3. 2011 Naslov: |
    |
|
|
[quote="vuja"]Jel može tko riješiti zadatak 1.33 pod a) (oni dolje za vježbu)? Elementaran primjer je, ali... Treba za provjeru :D Hvala :D
http://web.math.hr/nastava/analiza/files/ch1_3.pdf[/quote]
Za provjeru: [url=http://www.wolframalpha.com/input/?i=D(x^2/(1-x),+{x,+8})]WolframAlpha[/url].
Što se metode tiče, kod takvih zadataka je dobro prvo rastaviti na parcijalne razlomke. Konkretno, dovoljno je podijeliti dva polinoma: [latex]\displaystyle \frac{x^2}{1 - x} = -x - 1 + \frac{1}{1 - x}[/latex]. Indukcijom se lako provjeri da je [latex]\displaystyle \left( \frac{1}{1 - x} \right)^{(n)} = \frac{n!}{(1 - x)^{n + 1}}[/latex].
[quote="Vanja_"]Da li netko ima ideju kako bi rijesio ovaj prvi zadatak za n-tim derivacijama?
http://web.math.hr/nastava/analiza/kol/ma2-0708-kol1.pdf[/quote]
Iskoristi [latex]y' = 2 x \cos(x^2)[/latex], tj. [latex]\displaystyle \cos(x^2) = \frac{y'}{2 x}[/latex]. Kad se pojednostavi, dobi se [latex]x y'' - y' + 4 x^3 y = 0[/latex]. Trebala bi ispasti rekurzivna relacija [latex]y^{(n)}(0) = -4 (n - 1) (n - 3) y^{(n - 4)}(0)[/latex].
Drugi način je preko (ne)parnosti. Može se dokazati da je derivacija parne funkcije neparna, a neparne parna. Također se može pokazati da je derivacija parne funkcije u 0 jednaka 0. Vidimo da je zadana parna funkcija i traži se "parna derivacija" u 0, pa je rješenje 0.
Sad, pitanje je koliko su vam to asistenti istaknuli, tj. zahtijeva li se da sve to dokazujete na kolokviju. To treba njih pitati.
Edit: Da, glup sam. Ne zanima nas derivacija od [latex]f^{(100)}[/latex] u 0, već vrijednost u 0. :facepalm:
Za provjeru: WolframAlpha.
Što se metode tiče, kod takvih zadataka je dobro prvo rastaviti na parcijalne razlomke. Konkretno, dovoljno je podijeliti dva polinoma:  . Indukcijom se lako provjeri da je . Indukcijom se lako provjeri da je 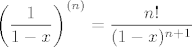 . .
Iskoristi 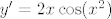 , tj. , tj. 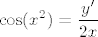 . Kad se pojednostavi, dobi se . Kad se pojednostavi, dobi se 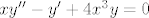 . Trebala bi ispasti rekurzivna relacija . Trebala bi ispasti rekurzivna relacija 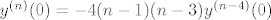 . .
Drugi način je preko (ne)parnosti. Može se dokazati da je derivacija parne funkcije neparna, a neparne parna. Također se može pokazati da je derivacija parne funkcije u 0 jednaka 0. Vidimo da je zadana parna funkcija i traži se "parna derivacija" u 0, pa je rješenje 0.
Sad, pitanje je koliko su vam to asistenti istaknuli, tj. zahtijeva li se da sve to dokazujete na kolokviju. To treba njih pitati.
Edit: Da, glup sam. Ne zanima nas derivacija od 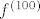 u 0, već vrijednost u 0. u 0, već vrijednost u 0. 
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:45 čet, 10. 3. 2011 Naslov: Postano: 19:45 čet, 10. 3. 2011 Naslov: |
    |
|
|
Okej, ideja za prvu grupu ide valjda ovako nekako: prebaci nazivnik na drugu stranu - sad imaš [latex]f(x)(1+e^{2x})=2x[/latex]. Sad, idemo stvar riješiti tzv. jakom indukcijom: lako ručno izračunamo da za recimo [latex]n=0[/latex] i [latex]n=1[/latex] tvrdnja vrijedi - to reci ako bude nekakav problem. E, sad pretpostavljamo da tvrdnja vrijedi za sve [latex]0\leq k\leq n-1[/latex] i želimo pokazati da onda vrijedi i za [latex]n[/latex] (mogli smo uzeti i da vrijedi do [latex]n[/latex], pa pokazivati za [latex]n+1[/latex], ali ovako mi se čini lakše za zapisati). Već smo pokazali za [latex]n=0[/latex] i [latex]n=1[/latex], pa možemo uzeti [latex]n\geq 2[/latex].
Gornji izraz deriviramo [latex]n[/latex] puta, s desne strane direktno, a slijeva Leibnizovom formulom. Dobivamo [latex]f^{(n)}(x)(1+e^{2x})+\sum_{k=0}^{n-1}\binom{n}{k}f^{(k)}(x)2^{n-k}e^{2x}=0[/latex], ako sam ja to sad dobro na brzinu izračunao (tu fale neki koraci, tako da si raspiši to slobodno :P).
Uvrstimo sad [latex]x=0[/latex] i dobivamo [latex]2f^{(n)}(0)+\sum_{k=0}^{n-1}\binom{n}{k}f^{(k)}(0)2^{n-k}=0[/latex]. Primijetimo sad da su, po indukcijskoj pretpostavci, svi [latex]f^{(k)}(0)[/latex] cijeli, pa je [latex]\sum_{k=0}^{n-1}\binom{n}{k}f^{(k)}(0)2^{n-k}[/latex] paran broj (svaki član ima barem jednu potenciju broja [latex]2[/latex] kraj sebe). No, onda je i [latex]2f^{(n)}(0)}[/latex] paran cijeli broj, pa je i [latex]f^{(n)}(0)[/latex] cijeli. Gotovo. :)
(Naravno, nigdje nisam posebno pripominjao da je [latex]f[/latex] proizvoljno mnogo puta derivabilna u [latex]0[/latex], što nije nebitno, ali se lako vidi, kao i u zadatku koji slijedi.)
Što se druge grupe tiče, ja bih išao nekako ovako (ne tvrdim baš da je to najbolji način, ali slično je ovome gore). Ponovno, za recimo [latex]n=1[/latex] i [latex]n=2[/latex] izračunamo ručno, da se ne moramo s time mučiti. Opet ćemo ići jakom indukcijom - pretpostavljamo da tvrdnja vrijedi za sve [latex]k\leq n[/latex] i pokazujemo ju za [latex]n+1[/latex]. E, sad, dalje primijeti (do toga se dosta prirodno dođe ili kvadriranjem pa deriviranjem ili čisto deriviranjem... nije neka mudrost, uglavnom :)) da vrijedi [latex]f(x)\cdot f'(x)=x[/latex]. Sad, derivirajmo to [latex]n[/latex] puta. Dobivamo (osim za [latex]n=1[/latex], što smo već razriješili prije, kao i u prvom zadatku) [latex]\sum_{k=0}^n\binom{n}{k}f^{(k)}(x)f^{(n-k+1)}(x)=0[/latex], tj. [latex]f(x)\cdot f^({n+1})+\sum_{k=1}^n\binom{n}{k}f^{(k)}(x)f^{(n-k+1)}{(x)=0[/latex]. E, sad, gledajmo predznake od ovoga tu - možeš razdijeliti na slučaj kad je [latex]n[/latex] paran i slučaj kad je neparan, na primjer. Ako je paran, [latex]k[/latex] i [latex]n+1-k[/latex] bit će različite parnosti, pa ćemo u svim produktima oblika [latex]f^{(k)}(x)f^{(n-k+1)}(x)[/latex] imati, po indukciji, negativan broj (ponovno, raspiši ako treba). To znači da, kad prebacimo na drugu stranu, [latex]f(x)\cdot f^({n+1})=-\sum_{k=1}^n\binom{n}{k}f^{(k)}(x)f^{(n-k+1)}(x)>0[/latex] odnosno, zbog [latex]f(x)>0[/latex], [latex]f^{(n+1)}(x)=(-1)^{n}f^{(n+1)}(x)>0[/latex]. Dakle, tvrdnja indukcije u ovom slučaju stoji.
Ako je [latex]n[/latex] neparan, potpuno analogno (jer su [latex]k[/latex] i [latex]n+1-k[/latex] iste parnosti, pa su ovi produkti pozitivni) dobivaš [latex]f(x)\cdot f^{(n+1)}=-\sum_{k=1}^n\binom{n}{k}f^({k})(x)f^{(n-k+1)}(x)<0[/latex]. Dakle, [latex]-f^{(n+1)}(x)=(-1)^{n}f^{(n+1)}(x)>0[/latex].
Eto, to je valjda to. :)
Okej, ideja za prvu grupu ide valjda ovako nekako: prebaci nazivnik na drugu stranu - sad imaš 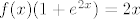 . Sad, idemo stvar riješiti tzv. jakom indukcijom: lako ručno izračunamo da za recimo . Sad, idemo stvar riješiti tzv. jakom indukcijom: lako ručno izračunamo da za recimo  i i 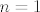 tvrdnja vrijedi - to reci ako bude nekakav problem. E, sad pretpostavljamo da tvrdnja vrijedi za sve tvrdnja vrijedi - to reci ako bude nekakav problem. E, sad pretpostavljamo da tvrdnja vrijedi za sve  i želimo pokazati da onda vrijedi i za i želimo pokazati da onda vrijedi i za  (mogli smo uzeti i da vrijedi do (mogli smo uzeti i da vrijedi do  , pa pokazivati za , pa pokazivati za 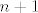 , ali ovako mi se čini lakše za zapisati). Već smo pokazali za , ali ovako mi se čini lakše za zapisati). Već smo pokazali za  i i 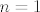 , pa možemo uzeti , pa možemo uzeti 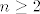 . .
Gornji izraz deriviramo  puta, s desne strane direktno, a slijeva Leibnizovom formulom. Dobivamo puta, s desne strane direktno, a slijeva Leibnizovom formulom. Dobivamo 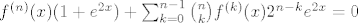 , ako sam ja to sad dobro na brzinu izračunao (tu fale neki koraci, tako da si raspiši to slobodno , ako sam ja to sad dobro na brzinu izračunao (tu fale neki koraci, tako da si raspiši to slobodno  ). ).
Uvrstimo sad  i dobivamo i dobivamo  . Primijetimo sad da su, po indukcijskoj pretpostavci, svi . Primijetimo sad da su, po indukcijskoj pretpostavci, svi 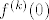 cijeli, pa je cijeli, pa je 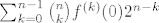 paran broj (svaki član ima barem jednu potenciju broja paran broj (svaki član ima barem jednu potenciju broja  kraj sebe). No, onda je i kraj sebe). No, onda je i 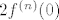 paran cijeli broj, pa je i paran cijeli broj, pa je i 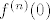 cijeli. Gotovo. cijeli. Gotovo. 
(Naravno, nigdje nisam posebno pripominjao da je  proizvoljno mnogo puta derivabilna u proizvoljno mnogo puta derivabilna u  , što nije nebitno, ali se lako vidi, kao i u zadatku koji slijedi.) , što nije nebitno, ali se lako vidi, kao i u zadatku koji slijedi.)
Što se druge grupe tiče, ja bih išao nekako ovako (ne tvrdim baš da je to najbolji način, ali slično je ovome gore). Ponovno, za recimo 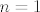 i i  izračunamo ručno, da se ne moramo s time mučiti. Opet ćemo ići jakom indukcijom - pretpostavljamo da tvrdnja vrijedi za sve izračunamo ručno, da se ne moramo s time mučiti. Opet ćemo ići jakom indukcijom - pretpostavljamo da tvrdnja vrijedi za sve 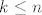 i pokazujemo ju za i pokazujemo ju za 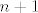 . E, sad, dalje primijeti (do toga se dosta prirodno dođe ili kvadriranjem pa deriviranjem ili čisto deriviranjem... nije neka mudrost, uglavnom . E, sad, dalje primijeti (do toga se dosta prirodno dođe ili kvadriranjem pa deriviranjem ili čisto deriviranjem... nije neka mudrost, uglavnom  ) da vrijedi ) da vrijedi 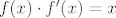 . Sad, derivirajmo to . Sad, derivirajmo to  puta. Dobivamo (osim za puta. Dobivamo (osim za 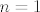 , što smo već razriješili prije, kao i u prvom zadatku) , što smo već razriješili prije, kao i u prvom zadatku) 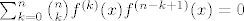 , tj. , tj. 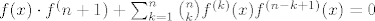 . E, sad, gledajmo predznake od ovoga tu - možeš razdijeliti na slučaj kad je . E, sad, gledajmo predznake od ovoga tu - možeš razdijeliti na slučaj kad je  paran i slučaj kad je neparan, na primjer. Ako je paran, paran i slučaj kad je neparan, na primjer. Ako je paran,  i i 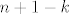 bit će različite parnosti, pa ćemo u svim produktima oblika bit će različite parnosti, pa ćemo u svim produktima oblika 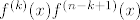 imati, po indukciji, negativan broj (ponovno, raspiši ako treba). To znači da, kad prebacimo na drugu stranu, imati, po indukciji, negativan broj (ponovno, raspiši ako treba). To znači da, kad prebacimo na drugu stranu, 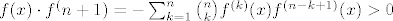 odnosno, zbog odnosno, zbog 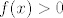 , ,  . Dakle, tvrdnja indukcije u ovom slučaju stoji. . Dakle, tvrdnja indukcije u ovom slučaju stoji.
Ako je  neparan, potpuno analogno (jer su neparan, potpuno analogno (jer su  i i 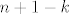 iste parnosti, pa su ovi produkti pozitivni) dobivaš iste parnosti, pa su ovi produkti pozitivni) dobivaš 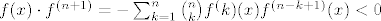 . Dakle, . Dakle, 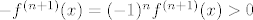 . .
Eto, to je valjda to. 
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
|












