|
Bok svima, evo kratka nadopuna prošlih demonstratura.
Riješavali smo kolokvij 2013.
1. Bilo je postavljeno pitanje može li se prvi zadatak riješiti koristeći Greenov teorem. Može - tako da gornji dio elipse nadopunimo segmentom na x-osi od -a do a. Postupak je bio valjan, samo mi se potkrala trivijalna greška prilikom računanja dvostrukog integrala (integrirao sam r, umjesto r^2). Inače je sve bilo u redu.
2. Nisam imao odmah dobru ideju za rješenje 6.c) zadatka pa nam je išlo malo teže. Uglavnom, evo alternative.
Prva alternativa je koristiti da je skup na kojem je forma zadana zvjezdast.
Naime, vrijedi teorem da je zatvorena forma egzaktna ukoliko je definirana na zvjezdastom skupu.
Ovaj skup je očito zvjezdast (izaberite neku točku na x osi - iz nje se može povući dužina u bilo koju drugu točku u tom skupu), forma je zatvorena i to je to.
Druga mogućnost je direktno preko Greenovog teorema. Ovo sam pokušavao na demonstraturama.
Htjeli bismo pokazati da integral forme ovisi samo o krajnim točkama puta. Ideja je nadopuniti put do zatvorenog puta. Predložio sam tada da se to napravi segmentima. To je moguće samo što onda ne možemo eksplicitno izračunati integrale - no to NIJE ni potrebno. Ako imamo integral po segmentu poanta je samo u tome da je to uvijek jedan te isti segment tj. vrijednost integrala je konstanta (koja god već bila). Neka je gamma proizvoljni put između nekih točaka A i B, a gamma_1 segmenti i gamma_2 segmenti koji spajaju točke s recimo točkom (1,0) na x-osi. Tada je
Znači [dtex]\int_\gamma+\int_{\gamma_1}+\int_{\gamma_2}=\iint_A d\omega=\iint_A=0[/dtex]
Iz toga se odmah dobije da je vrijednost integrala po gamma konstantna.
Još jedna mogućnost je sjetiti se da se kutna forma ponaša JAKO dobro ako u nju uvrstimo parametrizaciju kružnice. Pa je možda malo bolje ići po kružnici u pogledu same integracije.
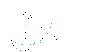
Neka imamo neke točke A i B i proizvoljan put između njih. Neka su polarne koordinate točke A(r, p) i B(R, q) i BSO r<R. Možemo ga nadopuniti do zatvorenog puta tako da uzmemo kružnicu oko ishodišta(!) za točku A, vučemo je do x-osi. Isto tako za točku B. Tada samo spojimo ta dva dijela nekim segmentom na x-osi. Na slici za primjer su to putevi gamma1,2,3.
Moguće je da ta zatvorena krivulja zatvara malo složenije područje kao na slici no naravno zbog aditivnosti integrala to ne igra nikakvu ulogu.
Napišimo sada parametrizaciju:
[tex]\gamma_1(t)=(r \cos t, r \sin t), t\in[0,p][/tex]
[tex]\gamma_2(t)=(t,0), t\in[r,R][/tex]
[tex]\gamma_3(t)=(R \cos t, R \sin t), t\in[q,0][/tex]
Onda napokon
[tex]\int_{\gamma}\omega+\int_{\gamma_1}\omega+\int{\gamma_2}\omega+\int{\gamma_3}\omega=\iint_A d\omega=\iint_A 0 =0[/tex]
Uvrste se parametrizacije gornjih puteva te se dobije da za proizvoljni put gamma vrijednost integrala je ista. Po teoremu s predavanja je to ekvivalentno egzkatnosti forme. Problem naravno s ovim načinom je što ovisi o poziciji točaka... npr. ovdje pretpostavljam da je točka A pod pozitivnim kutem, a B negativnim... ali naravno svi slučajevi su potpuno analogni pa i ovo uglavnom riješava zadatak. Stavljam u attach primjer ove nadopune iz 3. zadatka, nije ništa posebno.
I to je sve zasad :)
Bok svima, evo kratka nadopuna prošlih demonstratura.
Riješavali smo kolokvij 2013.
1. Bilo je postavljeno pitanje može li se prvi zadatak riješiti koristeći Greenov teorem. Može - tako da gornji dio elipse nadopunimo segmentom na x-osi od -a do a. Postupak je bio valjan, samo mi se potkrala trivijalna greška prilikom računanja dvostrukog integrala (integrirao sam r, umjesto r^2). Inače je sve bilo u redu.
2. Nisam imao odmah dobru ideju za rješenje 6.c) zadatka pa nam je išlo malo teže. Uglavnom, evo alternative.
Prva alternativa je koristiti da je skup na kojem je forma zadana zvjezdast.
Naime, vrijedi teorem da je zatvorena forma egzaktna ukoliko je definirana na zvjezdastom skupu.
Ovaj skup je očito zvjezdast (izaberite neku točku na x osi - iz nje se može povući dužina u bilo koju drugu točku u tom skupu), forma je zatvorena i to je to.
Druga mogućnost je direktno preko Greenovog teorema. Ovo sam pokušavao na demonstraturama.
Htjeli bismo pokazati da integral forme ovisi samo o krajnim točkama puta. Ideja je nadopuniti put do zatvorenog puta. Predložio sam tada da se to napravi segmentima. To je moguće samo što onda ne možemo eksplicitno izračunati integrale - no to NIJE ni potrebno. Ako imamo integral po segmentu poanta je samo u tome da je to uvijek jedan te isti segment tj. vrijednost integrala je konstanta (koja god već bila). Neka je gamma proizvoljni put između nekih točaka A i B, a gamma_1 segmenti i gamma_2 segmenti koji spajaju točke s recimo točkom (1,0) na x-osi. Tada je
Znači [dtex]\int_\gamma+\int_{\gamma_1}+\int_{\gamma_2}=\iint_A d\omega=\iint_A=0[/dtex]
Iz toga se odmah dobije da je vrijednost integrala po gamma konstantna.
Još jedna mogućnost je sjetiti se da se kutna forma ponaša JAKO dobro ako u nju uvrstimo parametrizaciju kružnice. Pa je možda malo bolje ići po kružnici u pogledu same integracije.
Neka imamo neke točke A i B i proizvoljan put između njih. Neka su polarne koordinate točke A(r, p) i B(R, q) i BSO r<R. Možemo ga nadopuniti do zatvorenog puta tako da uzmemo kružnicu oko ishodišta(!) za točku A, vučemo je do x-osi. Isto tako za točku B. Tada samo spojimo ta dva dijela nekim segmentom na x-osi. Na slici za primjer su to putevi gamma1,2,3.
Moguće je da ta zatvorena krivulja zatvara malo složenije područje kao na slici no naravno zbog aditivnosti integrala to ne igra nikakvu ulogu.
Napišimo sada parametrizaciju:
[tex]\gamma_1(t)=(r \cos t, r \sin t), t\in[0,p][/tex]
[tex]\gamma_2(t)=(t,0), t\in[r,R][/tex]
[tex]\gamma_3(t)=(R \cos t, R \sin t), t\in[q,0][/tex]
Onda napokon
[tex]\int_{\gamma}\omega+\int_{\gamma_1}\omega+\int{\gamma_2}\omega+\int{\gamma_3}\omega=\iint_A d\omega=\iint_A 0 =0[/tex]
Uvrste se parametrizacije gornjih puteva te se dobije da za proizvoljni put gamma vrijednost integrala je ista. Po teoremu s predavanja je to ekvivalentno egzkatnosti forme. Problem naravno s ovim načinom je što ovisi o poziciji točaka... npr. ovdje pretpostavljam da je točka A pod pozitivnim kutem, a B negativnim... ali naravno svi slučajevi su potpuno analogni pa i ovo uglavnom riješava zadatak. Stavljam u attach primjer ove nadopune iz 3. zadatka, nije ništa posebno.
I to je sve zasad 
| Description: |
|
| Filesize: |
51.46 KB |
| Viewed: |
398 Time(s) |
|
|




