| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Kento
Forumaš(ica)

Pridružen/a: 19. 09. 2012. (13:29:11)
Postovi: (2A)16
|
 Postano: 22:17 čet, 4. 6. 2015 Naslov: 2. kolokvij 2014./2015. Postano: 22:17 čet, 4. 6. 2015 Naslov: 2. kolokvij 2014./2015. |
    |
|
|
U prilogu se nalaze rješenja jedne grupe s prošlogodišnjeg kolokvija ("[i]inženjerska varijanta[/i]", no kolokvij za nastavnički smjer je relativno sličan). Ukoliko imate bilo kakvih pitanja u vezi rješenja (ili primijetite neku grešku), slobodno me kontaktirajte mailom. Svima želim puno sreće (bolje rečeno, znanja) na kolokviju!
U prilogu se nalaze rješenja jedne grupe s prošlogodišnjeg kolokvija ("inženjerska varijanta", no kolokvij za nastavnički smjer je relativno sličan). Ukoliko imate bilo kakvih pitanja u vezi rješenja (ili primijetite neku grešku), slobodno me kontaktirajte mailom. Svima želim puno sreće (bolje rečeno, znanja) na kolokviju!
| Description: |
|

Download |
| Filename: |
ka_kol2_2014_ing.pdf |
| Filesize: |
75.16 KB |
| Downloaded: |
1627 Time(s) |
|
|
| [Vrh] |
|
Kento
Forumaš(ica)

Pridružen/a: 19. 09. 2012. (13:29:11)
Postovi: (2A)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Kento
Forumaš(ica)

Pridružen/a: 19. 09. 2012. (13:29:11)
Postovi: (2A)16
|
 Postano: 21:45 uto, 16. 6. 2015 Naslov: Postano: 21:45 uto, 16. 6. 2015 Naslov: |
    |
|
|
[quote="Anonymous"][quote="Kento"]Ispravak u 3. zadatku: budući da je područje integracije krug radijusa [latex]\frac{3}{2}\pi[/latex], podintegralna funkcija ima još dva singulariteta, [latex]-\pi[/latex] i [latex]\pi[/latex], unutar [latex]\Gamma[/latex] (to su polovi 1. reda). Dakle, rješenju koje sam napisao treba dodati još i reziduume podintegralne funkcije u tim singularitetima (pomnožene s )[latex]2\pi i[/latex].[/quote]
jel moze sad pomoc kako jos te singularitete rijesiti u pi i -pi. Jesu to polovi 1.reda? Da li zapisem sinz kao -sin(z-pi) pa mi onda sinz(z-pi)/z-pi ide u 1?[/quote]
Da, tako je. To su polovi 1. reda, i korištenjem formule redukcije [latex]\sin z=-\sin(z-\pi)[/latex] koja je navedena se dobiju traženi reziduumi.
| Anonymous (napisa): | | Kento (napisa): | Ispravak u 3. zadatku: budući da je područje integracije krug radijusa 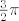 , podintegralna funkcija ima još dva singulariteta, , podintegralna funkcija ima još dva singulariteta, 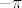 i i  , unutar , unutar 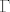 (to su polovi 1. reda). Dakle, rješenju koje sam napisao treba dodati još i reziduume podintegralne funkcije u tim singularitetima (pomnožene s ) (to su polovi 1. reda). Dakle, rješenju koje sam napisao treba dodati još i reziduume podintegralne funkcije u tim singularitetima (pomnožene s ) . . |
jel moze sad pomoc kako jos te singularitete rijesiti u pi i -pi. Jesu to polovi 1.reda? Da li zapisem sinz kao -sin(z-pi) pa mi onda sinz(z-pi)/z-pi ide u 1? |
Da, tako je. To su polovi 1. reda, i korištenjem formule redukcije 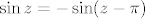 koja je navedena se dobiju traženi reziduumi. koja je navedena se dobiju traženi reziduumi.
|
|
| [Vrh] |
|
simon11
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (21:02:52)
Postovi: (7C)16
Spol: 
Lokacija: FunkyTown
|
|
| [Vrh] |
|
|





