| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 14:36 pon, 16. 8. 2004 Naslov: Postano: 14:36 pon, 16. 8. 2004 Naslov: |
    |
|
|
[quote="Anonymous"]Koji je od njih bliži stvarnoj vrijednosti površine ispod krivulje ?
Jeli to relativno ili jedan od njih ipak uvijek prednjači ?[/quote]
Relativno. :-s
Uzmi da je izmedju [i]a[/i] i [i]b[/i] parabola kojoj tjeme nije u sredini. :| Mislim da je jasno da se moze namjestiti da [latex]{f\left(\frac{a+b}{2}\right)}\cdot\left(b-a\right)[/latex] tocna povrsina ispod krivulje. :) Slicno mozes namjestiti i za drugu formulu, samo trenutno nemam inspiracije kako (ipak je jos rano ;)).
No, limesi, kad [i]n[/i] ide u beskonacno, su isti, pa to i nije tako bitno. 8)
| Anonymous (napisa): | Koji je od njih bliži stvarnoj vrijednosti površine ispod krivulje ?
Jeli to relativno ili jedan od njih ipak uvijek prednjači ? |
Relativno. 
Uzmi da je izmedju a i b parabola kojoj tjeme nije u sredini.  Mislim da je jasno da se moze namjestiti da Mislim da je jasno da se moze namjestiti da 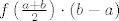 tocna povrsina ispod krivulje. tocna povrsina ispod krivulje.  Slicno mozes namjestiti i za drugu formulu, samo trenutno nemam inspiracije kako (ipak je jos rano Slicno mozes namjestiti i za drugu formulu, samo trenutno nemam inspiracije kako (ipak je jos rano  ). ).
No, limesi, kad n ide u beskonacno, su isti, pa to i nije tako bitno. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 12:07 pet, 27. 8. 2004 Naslov: Re: Razmatranja o integralu Postano: 12:07 pet, 27. 8. 2004 Naslov: Re: Razmatranja o integralu |
    |
|
|
[quote="Anonymous"]GRADIVO-INTEGRALI :
Zamislite si krivulju-graf funkcije iznad osi x,koja je neprekidna na segmentu [a,b].
Koji od ova dva broja bolje(preciznije) aproksimira površinu ispod grafa krivulje i zašto,koji je odnos ta dva broja ? :
(f(a)+f(b))/2 * (b-a)
ili
f( (a+b)/2 ) * (b-a)[/quote]
Kao što je već rečeno, ovisi. Evo konkretnih primjera:
(Označimo integral s I , a gornje brojeve s J i K redom.)
(BTW, vsego, za ovo što si ti namjeravao postići nisu ti dovoljne parabole, čak niti polinomi 3. stupnja - trebaš polinome stupnja bar 4 (ili neke funkcije koje nisu polinomi, naravno).)
Na intervalu [0,1] (da ne moramo množiti s b-a ; ):
f1(x):=5x^4-9x^2+5 => I=J=3<K=49/16
f2(x):=20x^4-33x^2+14 => I=K=7<J=15/2 .
Odnos između ta dva broja... također bilo koji. Za f1 je J<K , za f2 je J>K , a za bilo koju linearnu funkciju su jednaki.
(Inače... možda si zaboravio neke napomene o konveksnosti, konkavnosti... s njima bi zadatak mogao imati malo više smisla.; )
HTH,
| Anonymous (napisa): | GRADIVO-INTEGRALI :
Zamislite si krivulju-graf funkcije iznad osi x,koja je neprekidna na segmentu [a,b].
Koji od ova dva broja bolje(preciznije) aproksimira površinu ispod grafa krivulje i zašto,koji je odnos ta dva broja ? :
(f(a)+f(b))/2 * (b-a)
ili
f( (a+b)/2 ) * (b-a) |
Kao što je već rečeno, ovisi. Evo konkretnih primjera:
(Označimo integral s I , a gornje brojeve s J i K redom.)
(BTW, vsego, za ovo što si ti namjeravao postići nisu ti dovoljne parabole, čak niti polinomi 3. stupnja - trebaš polinome stupnja bar 4 (ili neke funkcije koje nisu polinomi, naravno).)
Na intervalu [0,1] (da ne moramo množiti s b-a ; ):
f1(x):=5x^4-9x^2+5 ⇒ I=J=3<K=49/16
f2(x):=20x^4-33x^2+14 ⇒ I=K=7<J=15/2 .
Odnos između ta dva broja... također bilo koji. Za f1 je J<K , za f2 je J>K , a za bilo koju linearnu funkciju su jednaki.
(Inače... možda si zaboravio neke napomene o konveksnosti, konkavnosti... s njima bi zadatak mogao imati malo više smisla.; )
HTH,
|
|
| [Vrh] |
|
|





