| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 12:23 ned, 22. 8. 2004 Naslov: Reimanov integral Postano: 12:23 ned, 22. 8. 2004 Naslov: Reimanov integral |
    |
|
|
Ovako,Reimanov teorem glasi :
[color=green]Pretpostavke : f:[a,b]->IR neprekidna
Doprinos teorema : onda je f (R)-integrabilna te postoji točka c sa
svojstvom Sf(x)dx=f(c)*(b-a) [/color]
(gdje je S oznaka za integral od a do b)
Pitanja:
1.U pretpostavci teorema zahtjevam omeđenu funkciju što je normalno jer samo za takve smo definirali (R)-integrabilnost,ali,zahtjevam užu klasu omeđenih funkcija odnosno upravo one koje su neprekidne na svojoj domeni.
Meni svojstvo neprekidnosti funkcije u dokazu treba i što onda ja mogu zaključiti ?
Da nitko nije uspio dokazati teorem bez toga svojstva ?
Da ipak postoji identičan teorem s tom razlikom da nije potrebna neprekidnost već jednostavno opća omeđenost ?
Nešto treće ?
2.Nije li točka c sa gore navedenim svojstvom vrlo zgodna za računanje integrala ?
Naravno problem je naći taj dragulj u moru ostalih točaka jeli ? :D
Naravno pritom ne mislim na traženje takvih dragulja za konstantnu funkciju jer je u tom slučaju more krcato istima. :lol:
Ovako,Reimanov teorem glasi :
Pretpostavke : f:[a,b]->IR neprekidna
Doprinos teorema : onda je f (R)-integrabilna te postoji točka c sa
svojstvom Sf(x)dx=f(c)*(b-a)
(gdje je S oznaka za integral od a do b)
Pitanja:
1.U pretpostavci teorema zahtjevam omeđenu funkciju što je normalno jer samo za takve smo definirali (R)-integrabilnost,ali,zahtjevam užu klasu omeđenih funkcija odnosno upravo one koje su neprekidne na svojoj domeni.
Meni svojstvo neprekidnosti funkcije u dokazu treba i što onda ja mogu zaključiti ?
Da nitko nije uspio dokazati teorem bez toga svojstva ?
Da ipak postoji identičan teorem s tom razlikom da nije potrebna neprekidnost već jednostavno opća omeđenost ?
Nešto treće ?
2.Nije li točka c sa gore navedenim svojstvom vrlo zgodna za računanje integrala ?
Naravno problem je naći taj dragulj u moru ostalih točaka jeli ? 
Naravno pritom ne mislim na traženje takvih dragulja za konstantnu funkciju jer je u tom slučaju more krcato istima. 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 13:15 ned, 22. 8. 2004 Naslov: Re: Reimanov integral Postano: 13:15 ned, 22. 8. 2004 Naslov: Re: Reimanov integral |
    |
|
|
[quote="Vincent Van Ear"]Ovako,Reimanov teorem glasi :
[color=green]Pretpostavke : f:[a,b]->IR neprekidna
Doprinos teorema : onda je f (R)-integrabilna te postoji točka c sa
svojstvom [latex]\int_a^b f(x)dx = f(c)*(b-a)[/latex] [/color][/quote]
[quote="Vincent Van Ear"]1.U pretpostavci teorema zahtjevam omeđenu funkciju što je normalno jer samo za takve smo definirali (R)-integrabilnost,ali,zahtjevam užu klasu omeđenih funkcija odnosno upravo one koje su neprekidne na svojoj domeni.
Meni svojstvo neprekidnosti funkcije u dokazu treba i što onda ja mogu zaključiti ?
Da nitko nije uspio dokazati teorem bez toga svojstva ?[/quote]
Mislim da je na ovom podforumu netko davnih dana nasao fju koja nije neprekidna ali je integrabilna :-k ...ili je to bilo, derivabilna fja, a ne samo neprekidna :-k ne znam vise :?
Al u svakom slucaju :D
Nitko nije rekao da vrijedi obrat teorema :) (tj. da je svaka (R)-integrabilna fja na segmentu neprekidna) Ono sto teorem kaze, jest, da ako imamo neprekidnost na segmentu, da tada mozemo sigurno zakljuciti i da je ta fja (R)-integrabilna.
Svojstvo neprekidnosti ti treba za ogranicenost :!: (BW tm za nepr fje) a treba ti i za uniformnu neprekidnost, koja se, mislim, koristi (ako se dobro sijecam) pri dokazu ovog teorema kojeg si naveo
[quote="Vincent Van Ear"]2.Nije li točka c sa gore navedenim svojstvom vrlo zgodna za računanje integrala ?
Naravno problem je naći taj dragulj u moru ostalih točaka jeli ? :D
Naravno pritom ne mislim na traženje takvih dragulja za konstantnu funkciju jer je u tom slučaju more krcato istima. :lol:[/quote]
Da... :) Gornja tocka, na kraju krajeva :) i nije bas TOLKO korisna, bar kolko ja znam za sada :) Al nagledat ces se svakakvih metoda pribliznog racunanja integrala, kada ce i ovaj teorem doci na povrsinu :roll: :)
btw, a i OT, postoji nesto sto se zove Cauchyeva integralna formula, koja je i jako primijenjiva, ali o tome vise na kompleksnoj analizi ;)
| Vincent Van Ear (napisa): | Ovako,Reimanov teorem glasi :
Pretpostavke : f:[a,b]→IR neprekidna
Doprinos teorema : onda je f (R)-integrabilna te postoji točka c sa
svojstvom 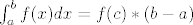 |
| Vincent Van Ear (napisa): | 1.U pretpostavci teorema zahtjevam omeđenu funkciju što je normalno jer samo za takve smo definirali (R)-integrabilnost,ali,zahtjevam užu klasu omeđenih funkcija odnosno upravo one koje su neprekidne na svojoj domeni.
Meni svojstvo neprekidnosti funkcije u dokazu treba i što onda ja mogu zaključiti ?
Da nitko nije uspio dokazati teorem bez toga svojstva ? |
Mislim da je na ovom podforumu netko davnih dana nasao fju koja nije neprekidna ali je integrabilna  ...ili je to bilo, derivabilna fja, a ne samo neprekidna ...ili je to bilo, derivabilna fja, a ne samo neprekidna  ne znam vise ne znam vise 
Al u svakom slucaju 
Nitko nije rekao da vrijedi obrat teorema  (tj. da je svaka (R)-integrabilna fja na segmentu neprekidna) Ono sto teorem kaze, jest, da ako imamo neprekidnost na segmentu, da tada mozemo sigurno zakljuciti i da je ta fja (R)-integrabilna. (tj. da je svaka (R)-integrabilna fja na segmentu neprekidna) Ono sto teorem kaze, jest, da ako imamo neprekidnost na segmentu, da tada mozemo sigurno zakljuciti i da je ta fja (R)-integrabilna.
Svojstvo neprekidnosti ti treba za ogranicenost  (BW tm za nepr fje) a treba ti i za uniformnu neprekidnost, koja se, mislim, koristi (ako se dobro sijecam) pri dokazu ovog teorema kojeg si naveo (BW tm za nepr fje) a treba ti i za uniformnu neprekidnost, koja se, mislim, koristi (ako se dobro sijecam) pri dokazu ovog teorema kojeg si naveo
| Vincent Van Ear (napisa): | 2.Nije li točka c sa gore navedenim svojstvom vrlo zgodna za računanje integrala ?
Naravno problem je naći taj dragulj u moru ostalih točaka jeli ? 
Naravno pritom ne mislim na traženje takvih dragulja za konstantnu funkciju jer je u tom slučaju more krcato istima.  |
Da...  Gornja tocka, na kraju krajeva Gornja tocka, na kraju krajeva  i nije bas TOLKO korisna, bar kolko ja znam za sada i nije bas TOLKO korisna, bar kolko ja znam za sada  Al nagledat ces se svakakvih metoda pribliznog racunanja integrala, kada ce i ovaj teorem doci na povrsinu Al nagledat ces se svakakvih metoda pribliznog racunanja integrala, kada ce i ovaj teorem doci na povrsinu  
btw, a i OT, postoji nesto sto se zove Cauchyeva integralna formula, koja je i jako primijenjiva, ali o tome vise na kompleksnoj analizi 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 13:17 ned, 22. 8. 2004 Naslov: Re: Reimanov integral Postano: 13:17 ned, 22. 8. 2004 Naslov: Re: Reimanov integral |
    |
|
|
[quote="Vincent Van Ear"]
1.U pretpostavci teorema zahtjevam omeđenu funkciju što je normalno jer samo za takve smo definirali (R)-integrabilnost,ali,zahtjevam užu klasu omeđenih funkcija odnosno upravo one koje su neprekidne na svojoj domeni.
Meni svojstvo neprekidnosti funkcije u dokazu treba i što onda ja mogu zaključiti ?
Da nitko nije uspio dokazati teorem bez toga svojstva ?
Da ipak postoji identičan teorem s tom razlikom da nije potrebna neprekidnost već jednostavno opća omeđenost ?
Nešto treće ?
[/quote]
U ovom slucaju, jednostavno je dati primjer funkcije koja je omedjena i nije neprekidna i da za nju ne vrijedi teorem. Dakle, promotrimo funkciju f:[-1,1]->|R, f(x)=-1 za x<0, f(x)=1 za x>=0. Ocito je integral te funkcije (u granicama -1, 1) jednak 0, a ne postoji tocka c@[-1,1] sa svojstvom iz teorema.
[quote="Vincent Van Ear"]
2.Nije li točka c sa gore navedenim svojstvom vrlo zgodna za računanje integrala ?
Naravno problem je naći taj dragulj u moru ostalih točaka jeli ?[/quote]
Je, to je veliki problem, jer kako mi se cini, egzistencija te tocke slijedi iz Bolzano-Weierstrassovog teorema, ciji dokaz (kao i vecina dokaza u analizi) nije konstruktivan, tako da je najjednostavnije pomiriti se s tim da tu tocku neces naci nista lakse nego sto ces rjesiti integral bez trazenja te tocke :cool:
| Vincent Van Ear (napisa): |
1.U pretpostavci teorema zahtjevam omeđenu funkciju što je normalno jer samo za takve smo definirali (R)-integrabilnost,ali,zahtjevam užu klasu omeđenih funkcija odnosno upravo one koje su neprekidne na svojoj domeni.
Meni svojstvo neprekidnosti funkcije u dokazu treba i što onda ja mogu zaključiti ?
Da nitko nije uspio dokazati teorem bez toga svojstva ?
Da ipak postoji identičan teorem s tom razlikom da nije potrebna neprekidnost već jednostavno opća omeđenost ?
Nešto treće ?
|
U ovom slucaju, jednostavno je dati primjer funkcije koja je omedjena i nije neprekidna i da za nju ne vrijedi teorem. Dakle, promotrimo funkciju f:[-1,1]→|R, f(x)=-1 za x<0, f(x)=1 za x>=0. Ocito je integral te funkcije (u granicama -1, 1) jednak 0, a ne postoji tocka c@[-1,1] sa svojstvom iz teorema.
| Vincent Van Ear (napisa): |
2.Nije li točka c sa gore navedenim svojstvom vrlo zgodna za računanje integrala ?
Naravno problem je naći taj dragulj u moru ostalih točaka jeli ? |
Je, to je veliki problem, jer kako mi se cini, egzistencija te tocke slijedi iz Bolzano-Weierstrassovog teorema, ciji dokaz (kao i vecina dokaza u analizi) nije konstruktivan, tako da je najjednostavnije pomiriti se s tim da tu tocku neces naci nista lakse nego sto ces rjesiti integral bez trazenja te tocke 
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 13:35 ned, 22. 8. 2004 Naslov: Re: Reimanov integral Postano: 13:35 ned, 22. 8. 2004 Naslov: Re: Reimanov integral |
    |
|
|
Vidim da su Zub i Doko odgovorili, ali mi je zao brisati ovoliko texta... :g:
[quote="Vincent Van Ear"]1.U pretpostavci teorema zahtjevam omeđenu funkciju što je normalno jer samo za takve smo definirali (R)-integrabilnost,ali,zahtjevam užu klasu omeđenih funkcija odnosno upravo one koje su neprekidne na svojoj domeni.
Meni svojstvo neprekidnosti funkcije u dokazu treba i što onda ja mogu zaključiti ?
Da nitko nije uspio dokazati teorem bez toga svojstva ?[/quote]
Tesko. :) Recimo, ako imas konacno mnogo prekida, onda gledas neprekidne dijelove i racunas integral kao sumu integrala tih dijelova, ne? ;)
Ono za sto ti treba neprekidnost je tocka c (koja je, btw, iz <a,b>, ako se ne varam). :o Recimo, funkcija f: [0,2]->|R
f(x) = 0, x < 1
f(x) = 1, x >= 1
Funkcija [b]je[/b] integrabilna (iako nije neprekidna), ali ne postoji c takav da je Sf(x)dx=1=f(c)(b-a)=2f(c) => f(c)=1/2
[quote="Vincent Van Ear"]Da ipak postoji identičan teorem s tom razlikom da nije potrebna neprekidnost već jednostavno opća omeđenost ?[/quote]
Iz protuprimjera je jasno da ne postoji [b]identican[/b] teorem bez neprekidnosti. 8)
Jos gore: opca omedjenost ti ne daje cak ni R-integrabilnost! :shock:
Klasican primjer: f: |R->|R
f(x)=1, x racionalan
f(x)=0, x iracionalan
Ta nije R-integrabilna ni na jednom segmentu [a,b], a<b. :)
[quote="Vincent Van Ear"]2.Nije li točka c sa gore navedenim svojstvom vrlo zgodna za računanje integrala ?[/quote]
Je. :g:
[quote="Vincent Van Ear"]Naravno problem je naći taj dragulj u moru ostalih točaka jeli ? :D[/quote]
U matematici je cesto dovoljno samo da nesto postoji. 8) Trazenje odredjenog c-a prepustamo drugima (fizicarima, na primjer ;)).
Vidim da su Zub i Doko odgovorili, ali mi je zao brisati ovoliko texta... 
| Vincent Van Ear (napisa): | 1.U pretpostavci teorema zahtjevam omeđenu funkciju što je normalno jer samo za takve smo definirali (R)-integrabilnost,ali,zahtjevam užu klasu omeđenih funkcija odnosno upravo one koje su neprekidne na svojoj domeni.
Meni svojstvo neprekidnosti funkcije u dokazu treba i što onda ja mogu zaključiti ?
Da nitko nije uspio dokazati teorem bez toga svojstva ? |
Tesko.  Recimo, ako imas konacno mnogo prekida, onda gledas neprekidne dijelove i racunas integral kao sumu integrala tih dijelova, ne? Recimo, ako imas konacno mnogo prekida, onda gledas neprekidne dijelove i racunas integral kao sumu integrala tih dijelova, ne? 
Ono za sto ti treba neprekidnost je tocka c (koja je, btw, iz <a,b>, ako se ne varam).  Recimo, funkcija f: [0,2]→|R Recimo, funkcija f: [0,2]→|R
f(x) = 0, x < 1
f(x) = 1, x >= 1
Funkcija je integrabilna (iako nije neprekidna), ali ne postoji c takav da je Sf(x)dx=1=f(c)(b-a)=2f(c) ⇒ f(c)=1/2
| Vincent Van Ear (napisa): | | Da ipak postoji identičan teorem s tom razlikom da nije potrebna neprekidnost već jednostavno opća omeđenost ? |
Iz protuprimjera je jasno da ne postoji identican teorem bez neprekidnosti. 
Jos gore: opca omedjenost ti ne daje cak ni R-integrabilnost! 
Klasican primjer: f: |R→|R
f(x)=1, x racionalan
f(x)=0, x iracionalan
Ta nije R-integrabilna ni na jednom segmentu [a,b], a<b. 
| Vincent Van Ear (napisa): | | 2.Nije li točka c sa gore navedenim svojstvom vrlo zgodna za računanje integrala ? |
Je. 
| Vincent Van Ear (napisa): | Naravno problem je naći taj dragulj u moru ostalih točaka jeli ?  |
U matematici je cesto dovoljno samo da nesto postoji.  Trazenje odredjenog c-a prepustamo drugima (fizicarima, na primjer Trazenje odredjenog c-a prepustamo drugima (fizicarima, na primjer  ). ).
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
|






