| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 0:22 ned, 29. 8. 2004 Naslov: Još jedan teoremčić u vezi s integralima Postano: 0:22 ned, 29. 8. 2004 Naslov: Još jedan teoremčić u vezi s integralima |
    |
|
|
[color=green]Teorem:
Pretpostavke:f,g:[a,b]->IR (R)-integrabilne , v,w@IR
Doprinos:njihova linearna kombinacija je (R)-integrabilna funkcija te vrijedi:
aSb v*f + aSb w*g[/color]
Dokaz:
f i g (R)-integrabilne => f i g omeđene => v*f+w*g omeđena funkcija
f (R)-integrabilna =>(propozicija o limesu sume koja aproksimira integral)=> posoji niz {d'_n} subidivizija takav da je aSb f(x)dx =lim_{n->oo} s(d'_n)=lim_{n->oo} S(d'_n) i S(d'_n)-s(d'_n)=0
g (R)-integrabilna =>(propozicija o limesu sume koja aproksimira integral)=> posoji niz {d''_n} subidivizija takav da je aSb g(x)dx =lim_{n->oo} s(d''_n)=lim_{n->oo} S(d''_n) i S(d''_n)-s(d''_n)=0
d_n := d'_n U d''_n
=>primjenom toga niza subdivizija na funkciju v*f+w*g=h dobivamo S(d_n;h)-s(d_n;h) -> 0
jer je [color=violet]ograničen linearnom kombinacijom odgovarajućih limesa[/color]
[color=brown](Moja dilema:e sad ove riječi iznad me kopkaju: ja moram dobiti dakle ovo:
lim_{n->oo}d_n=v*lim_{n->oo}d'_n + lim_{n->oo}d''_n = v * aSb f(x)dx + w * aSb g(x)dx ,
kako si to _precizno_ objašnjavam(intuitivno mi je sasvim jasno,ali kada stvari treba precizno izgovoriti tu gubim moral)[/color]
=>kriterij integrabilnosti=>v*f+w*g je Reiman integrabilna
(Napomena: aSb je određeni integral u točkama od a do b)
Teorem:
Pretpostavke:f,g:[a,b]->IR (R)-integrabilne , v,w@IR
Doprinos:njihova linearna kombinacija je (R)-integrabilna funkcija te vrijedi:
aSb v*f + aSb w*g
Dokaz:
f i g (R)-integrabilne => f i g omeđene => v*f+w*g omeđena funkcija
f (R)-integrabilna =>(propozicija o limesu sume koja aproksimira integral)=> posoji niz {d'_n} subidivizija takav da je aSb f(x)dx =lim_{n->oo} s(d'_n)=lim_{n->oo} S(d'_n) i S(d'_n)-s(d'_n)=0
g (R)-integrabilna =>(propozicija o limesu sume koja aproksimira integral)=> posoji niz {d''_n} subidivizija takav da je aSb g(x)dx =lim_{n->oo} s(d''_n)=lim_{n->oo} S(d''_n) i S(d''_n)-s(d''_n)=0
d_n := d'_n U d''_n
=>primjenom toga niza subdivizija na funkciju v*f+w*g=h dobivamo S(d_n;h)-s(d_n;h) -> 0
jer je ograničen linearnom kombinacijom odgovarajućih limesa
(Moja dilema:e sad ove riječi iznad me kopkaju: ja moram dobiti dakle ovo:
lim_{n->oo}d_n=v*lim_{n->oo}d'_n + lim_{n->oo}d''_n = v * aSb f(x)dx + w * aSb g(x)dx ,
kako si to _precizno_ objašnjavam(intuitivno mi je sasvim jasno,ali kada stvari treba precizno izgovoriti tu gubim moral)
=>kriterij integrabilnosti=>v*f+w*g je Reiman integrabilna
(Napomena: aSb je određeni integral u točkama od a do b)
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 12:33 ned, 29. 8. 2004 Naslov: Re: Još jedan teoremčić u vezi s integralima Postano: 12:33 ned, 29. 8. 2004 Naslov: Re: Još jedan teoremčić u vezi s integralima |
    |
|
|
[quote="Vincent Van Ear"][color=green]Teorem:
Pretpostavke:f,g:[a,b]->IR (R)-integrabilne , v,w@IR
Doprinos:njihova linearna kombinacija je (R)-integrabilna funkcija te vrijedi:
aSb v*f + aSb w*g[/color][/quote]
Tu nisi nikakvu izjavu napisao. Vjerojatno si htio reći da vrijedi da je integral linearne kombinacije jednak linearnoj kombinaciji integrala (s istim koeficijentima).
[quote]Dokaz:
f i g (R)-integrabilne => f i g omeđene => v*f+w*g omeđena funkcija
f (R)-integrabilna =>(propozicija o limesu sume koja aproksimira integral)=> posoji niz {d'_n} subidivizija takav da je aSb f(x)dx =lim_{n->oo} s(d'_n)=lim_{n->oo} S(d'_n) i S(d'_n)-s(d'_n)=0[/quote]
Nije _jednako_ nuli, već _teži_ nuli (po n ).
[quote]g (R)-integrabilna =>(propozicija o limesu sume koja aproksimira integral)=> posoji niz {d''_n} subidivizija takav da je aSb g(x)dx =lim_{n->oo} s(d''_n)=lim_{n->oo} S(d''_n) i S(d''_n)-s(d''_n)=0[/quote]
Također.
[quote]d_n := d'_n U d''_n
=>primjenom toga niza subdivizija na funkciju v*f+w*g=h dobivamo S(d_n;h)-s(d_n;h) -> 0
jer je [color=violet]ograničen linearnom kombinacijom odgovarajućih limesa[/color]
[color=brown](Moja dilema:e sad ove riječi iznad me kopkaju: ja moram dobiti dakle ovo:
lim_{n->oo}d_n=v*lim_{n->oo}d'_n + lim_{n->oo}d''_n = v * aSb f(x)dx + w * aSb g(x)dx ,
kako si to _precizno_ objašnjavam(intuitivno mi je sasvim jasno,ali kada stvari treba precizno izgovoriti tu gubim moral)[/color][/quote]
Ovo što si gore napisao je glupost. Limesiraš i zbrajaš subdivizije :shock: .
Ono što tebi treba je sljedeće:
Prvo, pretpostavimo da su v i w nenegativni, te f i g nenegativne (ako nešto od toga može biti negativno, dokaz je malo kompliciraniji, ali ne puno). Lako se vidi da je tada za svaku dn ,
S(vf+wg,dn)=vS(f,dn)+wS(g,dn)<=vS(f,dn')+wS(g,dn'') i
s(vf+wg,dn)=vs(f,dn)+ws(g,dn)>=vs(f,dn')+ws(g,dn'') .
Oduzimanjem te dvije nejednakosti dobijemo
(S-s)(h,dn)<=v*(S-s)(f,dn')+w*(S-s)(g,dn'') .
Sada tvrdnja da lijeva strana teži u 0 slijedi iz činjenice da je nenegativna, teorema o sendviču i jednostavne činjenice o limesima
[latex]\lim_n(v\cdot a_n+w\cdot b_n)=v\cdot\lim_n a_n+w\cdot\lim_n b_n[/latex].
HTH,
| Vincent Van Ear (napisa): | Teorem:
Pretpostavke:f,g:[a,b]→IR (R)-integrabilne , v,w@IR
Doprinos:njihova linearna kombinacija je (R)-integrabilna funkcija te vrijedi:
aSb v*f + aSb w*g |
Tu nisi nikakvu izjavu napisao. Vjerojatno si htio reći da vrijedi da je integral linearne kombinacije jednak linearnoj kombinaciji integrala (s istim koeficijentima).
| Citat: | Dokaz:
f i g (R)-integrabilne ⇒ f i g omeđene ⇒ v*f+w*g omeđena funkcija
f (R)-integrabilna ⇒(propozicija o limesu sume koja aproksimira integral)⇒ posoji niz {d'_n} subidivizija takav da je aSb f(x)dx =lim_{n→oo} s(d'_n)=lim_{n→oo} S(d'_n) i S(d'_n)-s(d'_n)=0 |
Nije _jednako_ nuli, već _teži_ nuli (po n ).
| Citat: | | g (R)-integrabilna ⇒(propozicija o limesu sume koja aproksimira integral)⇒ posoji niz {d''_n} subidivizija takav da je aSb g(x)dx =lim_{n→oo} s(d''_n)=lim_{n→oo} S(d''_n) i S(d''_n)-s(d''_n)=0 |
Također.
| Citat: | d_n := d'_n U d''_n
⇒primjenom toga niza subdivizija na funkciju v*f+w*g=h dobivamo S(d_n;h)-s(d_n;h) → 0
jer je ograničen linearnom kombinacijom odgovarajućih limesa
(Moja dilema:e sad ove riječi iznad me kopkaju: ja moram dobiti dakle ovo:
lim_{n→oo}d_n=v*lim_{n→oo}d'_n + lim_{n→oo}d''_n = v * aSb f(x)dx + w * aSb g(x)dx ,
kako si to _precizno_ objašnjavam(intuitivno mi je sasvim jasno,ali kada stvari treba precizno izgovoriti tu gubim moral) |
Ovo što si gore napisao je glupost. Limesiraš i zbrajaš subdivizije  . .
Ono što tebi treba je sljedeće:
Prvo, pretpostavimo da su v i w nenegativni, te f i g nenegativne (ako nešto od toga može biti negativno, dokaz je malo kompliciraniji, ali ne puno). Lako se vidi da je tada za svaku dn ,
S(vf+wg,dn)=vS(f,dn)+wS(g,dn)⇐vS(f,dn')+wS(g,dn'') i
s(vf+wg,dn)=vs(f,dn)+ws(g,dn)>=vs(f,dn')+ws(g,dn'') .
Oduzimanjem te dvije nejednakosti dobijemo
(S-s)(h,dn)⇐v*(S-s)(f,dn')+w*(S-s)(g,dn'') .
Sada tvrdnja da lijeva strana teži u 0 slijedi iz činjenice da je nenegativna, teorema o sendviču i jednostavne činjenice o limesima
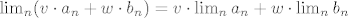 . .
HTH,
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 13:17 ned, 29. 8. 2004 Naslov: Postano: 13:17 ned, 29. 8. 2004 Naslov: |
    |
|
|
[quote]Ovo što si gore napisao je glupost. Limesiraš i zbrajaš subdivizije .[/quote]
Uh,pardon.
Dobro smijem ih samo limesirati…stvarno glupost-pa kako bih zbrajao (konačne) skupove...možda se i mogu ali ja to zasada neznam!
:shock:
[quote]Prvo, pretpostavimo da su v i w nenegativni, te f i g nenegativne (ako nešto od toga može biti negativno, dokaz je malo kompliciraniji, ali ne puno). Lako se vidi da je tada za svaku dn ,
S(vf+wg,dn)=vS(f,dn)+wS(g,dn)<=vS(f,dn')+wS(g,dn'') i
s(vf+wg,dn)=vs(f,dn)+ws(g,dn)>=vs(f,dn')+ws(g,dn'') .
Oduzimanjem te dvije nejednakosti dobijemo
(S-s)(h,dn)<=v*(S-s)(f,dn')+w*(S-s)(g,dn'') .
Sada tvrdnja da lijeva strana teži u 0 slijedi iz činjenice da je nenegativna, teorema o sendviču i jednostavne činjenice o limesima
.
HTH,[/quote]
Hvala. :wink:
| Citat: | | Ovo što si gore napisao je glupost. Limesiraš i zbrajaš subdivizije . |
Uh,pardon.
Dobro smijem ih samo limesirati…stvarno glupost-pa kako bih zbrajao (konačne) skupove...možda se i mogu ali ja to zasada neznam!

| Citat: | Prvo, pretpostavimo da su v i w nenegativni, te f i g nenegativne (ako nešto od toga može biti negativno, dokaz je malo kompliciraniji, ali ne puno). Lako se vidi da je tada za svaku dn ,
S(vf+wg,dn)=vS(f,dn)+wS(g,dn)⇐vS(f,dn')+wS(g,dn'') i
s(vf+wg,dn)=vs(f,dn)+ws(g,dn)>=vs(f,dn')+ws(g,dn'') .
Oduzimanjem te dvije nejednakosti dobijemo
(S-s)(h,dn)⇐v*(S-s)(f,dn')+w*(S-s)(g,dn'') .
Sada tvrdnja da lijeva strana teži u 0 slijedi iz činjenice da je nenegativna, teorema o sendviču i jednostavne činjenice o limesima
.
HTH, |
Hvala. 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
|




