|
[quote="Crni"]Ugrubo; mislim da bi trebalo izrazit površinu za neki proizvoljni x>0, pa onda [i]limesirat[/i] izraz u beskonačnost po x.[/quote]
Da, samo najveći dio posla je upravo ovaj prvi. :-)
Dakle, prvo se nađe asimptota. To ne bi trebalo biti tako strašno, standardni postupak za traženje kose asimptote, vjerujem da ga znaš. Dobije se y=x . Sad se nađu točke presjeka i visinski odnos asimptote i grafa naše funkcije. Rješavajući x=f(x) dobije se x=x^3 , odnosno x-evi presjeka su -1 , 0 i 1 . U prvom kvadrantu (lako se provjeri da je za x>0 ujedno i f(x)>0 ), dakle, trebat ćemo integrirati od 0 do 1 i od 1 do +oo .
Od 0 do 1 je x>f(x) (opet, jednostavno rješavanje nejednadžbi - primijeti da je nazivnik od f(x) uvijek pozitivan, pa možeš množiti njime) , pa je graf funkcije ispod asimptote - funkcija za integriranje je x-f(x) . Na <1,+oo> je obrnuto - graf funkcije je iznad asimptote, pa je funkcija f(x)-x .
Sve u svemu, ti tražiš
[latex]\int_0^1(x-(x^5+x^3)/(x^4+1))\,dx+\int_1^{+\infty}((x^5+x^3)/(x^4+1)-x)\,dx[/latex], što se lako dobije jednom kad se nađe primitivna funkcija tog podintegralnog čuda.
int_0^1(g)+int_1^+oo(-g)=G(1)-G(0)+lim{+oo}(-G)-(-G)(1)=
=2G(1)-G(0)-lim{+oo}G .
Čudo se svođenjem na zajednički nazivnik malo pojednostavi, pa imamo
x-(x^5+x^3)/(x^4+1)=(x-x^3)/(1+x^4) , što je još uvijek (prava) racionalna funkcija s kojom ima dosta posla, osim ako se čovjek sjeti gore izlučiti x^2 i to supstituirati pod t . :-)
Uglavnom, dobije se G(x)=arctg(x^2)/2-ln(1+x^4)/4 , što nažalost ide prema -oo kad x->+oo , dakle gornji integral ne postoji (divergira).
(In a way, može se reći da je površina +oo , no zapravo u okviru standardne MA1&2 nije definirana.)
HTH,
| Crni (napisa): | | Ugrubo; mislim da bi trebalo izrazit površinu za neki proizvoljni x>0, pa onda limesirat izraz u beskonačnost po x. |
Da, samo najveći dio posla je upravo ovaj prvi. 
Dakle, prvo se nađe asimptota. To ne bi trebalo biti tako strašno, standardni postupak za traženje kose asimptote, vjerujem da ga znaš. Dobije se y=x . Sad se nađu točke presjeka i visinski odnos asimptote i grafa naše funkcije. Rješavajući x=f(x) dobije se x=x^3 , odnosno x-evi presjeka su -1 , 0 i 1 . U prvom kvadrantu (lako se provjeri da je za x>0 ujedno i f(x)>0 ), dakle, trebat ćemo integrirati od 0 do 1 i od 1 do +oo .
Od 0 do 1 je x>f(x) (opet, jednostavno rješavanje nejednadžbi - primijeti da je nazivnik od f(x) uvijek pozitivan, pa možeš množiti njime) , pa je graf funkcije ispod asimptote - funkcija za integriranje je x-f(x) . Na <1,+oo> je obrnuto - graf funkcije je iznad asimptote, pa je funkcija f(x)-x .
Sve u svemu, ti tražiš
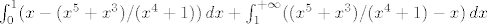 , što se lako dobije jednom kad se nađe primitivna funkcija tog podintegralnog čuda.
int_0^1(g)+int_1^+oo(-g)=G(1)-G(0)+lim{+oo}(-G)-(-G)(1)=
=2G(1)-G(0)-lim{+oo}G .
Čudo se svođenjem na zajednički nazivnik malo pojednostavi, pa imamo
x-(x^5+x^3)/(x^4+1)=(x-x^3)/(1+x^4) , što je još uvijek (prava) racionalna funkcija s kojom ima dosta posla, osim ako se čovjek sjeti gore izlučiti x^2 i to supstituirati pod t .
Uglavnom, dobije se G(x)=arctg(x^2)/2-ln(1+x^4)/4 , što nažalost ide prema -oo kad x→+oo , dakle gornji integral ne postoji (divergira).
(In a way, može se reći da je površina +oo , no zapravo u okviru standardne MA1&2 nije definirana.)
HTH,
|
Everything happens with a reason! 
