| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 20:27 pon, 27. 6. 2005 Naslov: Postano: 20:27 pon, 27. 6. 2005 Naslov: |
    |
|
|
Evo (da ne bude da samo ispitujem, a nikad ne napisem nista korisno) sto je bilo na mom usmenom.
Usput, bio je doc. Huzak koji vec godinu dana drzi Matematicku statistiku, ali cini se da se gradivo nije previse mijenjalo.
1. O BLUE (najboljem nepristranom linearnom procjenitelju), stvari vezane uz to, dokaz Gauss-Markovljevog teorema, sa razjasnjenjem svih stvari koje se tamo pojavljuju (npr. cov(AU)=Acov(U)A^t, nepristranost, Gauss-Markovljevi uvjeti itd.)
2. Testiranje hipoteze H_0: m1=m2 prema alternativi H_1: m1<m2, pri cemu su dana dva nezavisna uzorka: X_1,...,X_k iz modela s N(m1,s^2) distiribucijom i Y_1,...,Y_l iz modela s N(m2,s^2) (varijance su jednake). Izgradnja test statistike, pitanja vezana uz distribucije koje se tu pojavljuju (hi-kvadrat, normalna, studentova) i stvari vezane uz njih (npr. da za X~N(a,p) i Y~N(b,q) nezavisne vrijedi X-Y~N(a-b,p+q) i tome slicno). Odredjivanje kriticnog podrucja...
Eto, nadam se da ce nekome bar malo pomoci.
T.P.
Evo (da ne bude da samo ispitujem, a nikad ne napisem nista korisno) sto je bilo na mom usmenom.
Usput, bio je doc. Huzak koji vec godinu dana drzi Matematicku statistiku, ali cini se da se gradivo nije previse mijenjalo.
1. O BLUE (najboljem nepristranom linearnom procjenitelju), stvari vezane uz to, dokaz Gauss-Markovljevog teorema, sa razjasnjenjem svih stvari koje se tamo pojavljuju (npr. cov(AU)=Acov(U)A^t, nepristranost, Gauss-Markovljevi uvjeti itd.)
2. Testiranje hipoteze H_0: m1=m2 prema alternativi H_1: m1<m2, pri cemu su dana dva nezavisna uzorka: X_1,...,X_k iz modela s N(m1,s^2) distiribucijom i Y_1,...,Y_l iz modela s N(m2,s^2) (varijance su jednake). Izgradnja test statistike, pitanja vezana uz distribucije koje se tu pojavljuju (hi-kvadrat, normalna, studentova) i stvari vezane uz njih (npr. da za X~N(a,p) i Y~N(b,q) nezavisne vrijedi X-Y~N(a-b,p+q) i tome slicno). Odredjivanje kriticnog podrucja...
Eto, nadam se da ce nekome bar malo pomoci.
T.P.
|
|
| [Vrh] |
|
Gia
Forumaš(ica)

Pridružen/a: 20. 06. 2004. (00:46:02)
Postovi: (1D)16
|
 Postano: 22:25 pon, 27. 6. 2005 Naslov: Postano: 22:25 pon, 27. 6. 2005 Naslov: |
    |
|
|
Ja sam danas imala usmeni,pitao me je Kolmogorov-Smirnovljevu statistiku, standardni n-dim sl.vektor,pogresku druse vrste i snagu testa,pita takoder BLUE, gauss-markov tm, studentovu razdiobu,razne procjenitelje, sve tm sa imenima i tako.uglavnom pocme sa konkretnim pitanjem pa se nadovezujete.uglavnom pita neki test,prepoznat k.p. i testnu statistiku. prof je super,ne gnjavi pitanjima van biljeski sa predavanja, nauci predavanja i to je to.ako nesto zapne imas u knjizi prof.Zeljka Pausea ovaj zadnji dio jako dobro objasnjen. sretno
Ja sam danas imala usmeni,pitao me je Kolmogorov-Smirnovljevu statistiku, standardni n-dim sl.vektor,pogresku druse vrste i snagu testa,pita takoder BLUE, gauss-markov tm, studentovu razdiobu,razne procjenitelje, sve tm sa imenima i tako.uglavnom pocme sa konkretnim pitanjem pa se nadovezujete.uglavnom pita neki test,prepoznat k.p. i testnu statistiku. prof je super,ne gnjavi pitanjima van biljeski sa predavanja, nauci predavanja i to je to.ako nesto zapne imas u knjizi prof.Zeljka Pausea ovaj zadnji dio jako dobro objasnjen. sretno
_________________ 
Gia |
|
| [Vrh] |
|
decec
Forumaš(ica)

Pridružen/a: 20. 07. 2005. (01:10:53)
Postovi: (42)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
decec
Forumaš(ica)

Pridružen/a: 20. 07. 2005. (01:10:53)
Postovi: (42)16
Lokacija: Zagreb
|
 Postano: 23:52 sri, 28. 9. 2005 Naslov: Postano: 23:52 sri, 28. 9. 2005 Naslov: |
    |
|
|
:lol:
pa ti mene pratiš!
ali da, znam da su pmf-ovci ok (uglavnom),jer je na našem faxu čak 5 djelatnika u kabinetu za matematiku ,a bome se i najviše trude i redovito održavaju web.
http://www.pbf.hr/matematika/
on topic:
na usmenom voli pitati vjerojatnost,binomnu i normalnu razdiobu,mene je pitao E od X (očekivanje raznih funkcija i bla bla...) ...

pa ti mene pratiš!
ali da, znam da su pmf-ovci ok (uglavnom),jer je na našem faxu čak 5 djelatnika u kabinetu za matematiku ,a bome se i najviše trude i redovito održavaju web.
http://www.pbf.hr/matematika/
on topic:
na usmenom voli pitati vjerojatnost,binomnu i normalnu razdiobu,mene je pitao E od X (očekivanje raznih funkcija i bla bla...) ...
|
|
| [Vrh] |
|
mala
Gost
|
|
| [Vrh] |
|
Ivančica
Forumaš(ica)

Pridružen/a: 16. 04. 2003. (15:05:55)
Postovi: (255)16
Spol: 
Lokacija: ja sam ti ko zvrk - stalno sam drugdje
|
|
| [Vrh] |
|
Gost
|
 Postano: 17:34 uto, 12. 9. 2006 Naslov: Postano: 17:34 uto, 12. 9. 2006 Naslov: |
    |
|
|
mene je pitao donju cramer-rao granicu...u kakvim modelima to vrijedi,svojstva,znacenja tih svojstava...primjer neprekidne sl.var koja je iz tog modela,primjer diskretne...i onda me pitao fisherov test jer je on bio na pismenom...uglavnom profesor pogleda pismeni,pa zadatak koji je lose napisan pita teoriju oko toga...cula sam da je jako bitno znato one tm 6.11,12,13,14(to su tm koji nam tvrde kako dobijemo koju distribuciju preko uzoracke varijance i aritmeticke sredine)profesor je super,strpljiv i da dobre hintove...sretno!
mene je pitao donju cramer-rao granicu...u kakvim modelima to vrijedi,svojstva,znacenja tih svojstava...primjer neprekidne sl.var koja je iz tog modela,primjer diskretne...i onda me pitao fisherov test jer je on bio na pismenom...uglavnom profesor pogleda pismeni,pa zadatak koji je lose napisan pita teoriju oko toga...cula sam da je jako bitno znato one tm 6.11,12,13,14(to su tm koji nam tvrde kako dobijemo koju distribuciju preko uzoracke varijance i aritmeticke sredine)profesor je super,strpljiv i da dobre hintove...sretno!
|
|
| [Vrh] |
|
tara
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 15:06 uto, 5. 12. 2006 Naslov: Postano: 15:06 uto, 5. 12. 2006 Naslov: |
    |
|
|
Evo i pitanja sa današnjeg usmenog:
-Neyman-Pearsonova lema+dokaz
-Cramer-Rao +dokaz (objasniti C-S-B nejednakost)
-test X1,...,Xn1; Y1,...,Yn2 test o očekivanju(M-W-W) i varijanci(Fisher)-s vježbi
-sve o lin. reg. modelu, test statistika za theta s konstrukcijom i dokazom onoga što koristimo ; p.i.
-Kolm-Smirnov test; sto je procjenitelj za F?-->empirijska fja distribucije; malo o tome da je to neparametarski model ali mi gledamo F kao parametar
-O nezavisnosti aritmetičke sredine i uzoračke varijance i o distribucijama njih--->za Sn2 misli na ono do na konstantu pa tm za studentovu razdiobu s n-1 param. slobode
i dokaz ta 2 teorema
-Procjenitelj za parametre normalanog modela--> (aritm sredina, uzoračka varijanca)
-sve o regularnom modelu, objasniti što govori što i napisati one raspise nakom definicije koje trebaju u dokazu Cramer-Rao
Profesor je bio super i dobili smo puno lijepih ocjena!!!!!!!
Sretno!!!!!!!
Evo i pitanja sa današnjeg usmenog:
-Neyman-Pearsonova lema+dokaz
-Cramer-Rao +dokaz (objasniti C-S-B nejednakost)
-test X1,...,Xn1; Y1,...,Yn2 test o očekivanju(M-W-W) i varijanci(Fisher)-s vježbi
-sve o lin. reg. modelu, test statistika za theta s konstrukcijom i dokazom onoga što koristimo ; p.i.
-Kolm-Smirnov test; sto je procjenitelj za F?-->empirijska fja distribucije; malo o tome da je to neparametarski model ali mi gledamo F kao parametar
-O nezavisnosti aritmetičke sredine i uzoračke varijance i o distribucijama njih--->za Sn2 misli na ono do na konstantu pa tm za studentovu razdiobu s n-1 param. slobode
i dokaz ta 2 teorema
-Procjenitelj za parametre normalanog modela--> (aritm sredina, uzoračka varijanca)
-sve o regularnom modelu, objasniti što govori što i napisati one raspise nakom definicije koje trebaju u dokazu Cramer-Rao
Profesor je bio super i dobili smo puno lijepih ocjena!!!!!!!
Sretno!!!!!!!
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
|
| [Vrh] |
|
Tvrtko
Forumaš(ica)

Pridružen/a: 21. 10. 2006. (12:12:34)
Postovi: (10A)16
Lokacija: CCP 4345 / PMF-MO 225
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
 Postano: 17:01 ned, 10. 2. 2008 Naslov: Postano: 17:01 ned, 10. 2. 2008 Naslov: |
    |
|
|
opet ja :P
u zadaci kaj smo ju dobili, vezanoj za linearan regresijski model, zapinjem na 3.a) zadatku; naime, zapela sam kad trebam pokazati da je [latex]Cov(PX)=PP^{\tau}[/latex] jednako dijagonalnoj matrici koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule.
i da...kaj se tice drugog zadatka iz iste zadace; krenem od tog da se svaka simetricna matrica [latex]P[/latex] moze dijagonalizirati na nacin [latex]P=Q\Lambda Q^{\tau}[/latex], gdje je [latex]Q[/latex] ortogonalna i sadrzi svojstvene vektore od [latex]P[/latex], a [latex]\Lambda[/latex] dijagonalna sa svojstvenim vrijednostima od [latex]P[/latex]. zna netko kak sad natjerat da dobim za [latex]\Lambda[/latex] matricu koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule?
opet ja 
u zadaci kaj smo ju dobili, vezanoj za linearan regresijski model, zapinjem na 3.a) zadatku; naime, zapela sam kad trebam pokazati da je 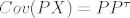 jednako dijagonalnoj matrici koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule. jednako dijagonalnoj matrici koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule.
i da...kaj se tice drugog zadatka iz iste zadace; krenem od tog da se svaka simetricna matrica  moze dijagonalizirati na nacin moze dijagonalizirati na nacin 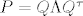 , gdje je , gdje je 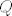 ortogonalna i sadrzi svojstvene vektore od ortogonalna i sadrzi svojstvene vektore od  , a , a 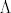 dijagonalna sa svojstvenim vrijednostima od dijagonalna sa svojstvenim vrijednostima od  . zna netko kak sad natjerat da dobim za . zna netko kak sad natjerat da dobim za 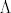 matricu koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule? matricu koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule?
_________________ Laganini...i stprljivo....  |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 23:21 pon, 11. 2. 2008 Naslov: Postano: 23:21 pon, 11. 2. 2008 Naslov: |
    |
|
|
[quote="Meri"]opet ja :P
u zadaci kaj smo ju dobili, vezanoj za linearan regresijski model, zapinjem na 3.a) zadatku; naime, zapela sam kad trebam pokazati da je [latex]Cov(PX)=PP^{\tau}[/latex] jednako dijagonalnoj matrici koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule.
i da...kaj se tice drugog zadatka iz iste zadace; krenem od tog da se svaka simetricna matrica [latex]P[/latex] moze dijagonalizirati na nacin [latex]P=Q\Lambda Q^{\tau}[/latex], gdje je [latex]Q[/latex] ortogonalna i sadrzi svojstvene vektore od [latex]P[/latex], a [latex]\Lambda[/latex] dijagonalna sa svojstvenim vrijednostima od [latex]P[/latex]. zna netko kak sad natjerat da dobim za [latex]\Lambda[/latex] matricu koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule?[/quote]
Evo da ja probam, nadam se da neću puno zbrljat.
Dakle, prema mojem skromnom mišljenju, ono prvo ne vrijedi, jer PP' ne mora općenito biti jednako takvoj matrici, ali to ne smeta da se dokaže sve ostalo.
Za drugo, sve svojstvene vrijednosti od P jesu 0 i 1, pa sad samo zamijeniš retke i stupce (valjda) u ovom umnošku matrica. Uglavnom, već smo na linearnoj pokazali da se to može. ne znam sad ovako napamet postupak da "natjeraš" 1 na jednu stranu a 0 na drugu, ali u osnovi smo na linearnoj pokazali da kako su joj samo 0 i 1 svojstvene vrijednosti (i simetrična je) da postoje ovakva ortogonalna matrica koja prevodi P u dijagonalnu sa svojstvenim vrijednostima na dijagonali i naravno tu si možeš narihtat bilo kakav poredak.
Nadam se da je pomoglo :?
| Meri (napisa): | opet ja 
u zadaci kaj smo ju dobili, vezanoj za linearan regresijski model, zapinjem na 3.a) zadatku; naime, zapela sam kad trebam pokazati da je 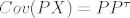 jednako dijagonalnoj matrici koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule. jednako dijagonalnoj matrici koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule.
i da...kaj se tice drugog zadatka iz iste zadace; krenem od tog da se svaka simetricna matrica  moze dijagonalizirati na nacin moze dijagonalizirati na nacin 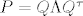 , gdje je , gdje je 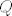 ortogonalna i sadrzi svojstvene vektore od ortogonalna i sadrzi svojstvene vektore od  , a , a 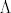 dijagonalna sa svojstvenim vrijednostima od dijagonalna sa svojstvenim vrijednostima od  . zna netko kak sad natjerat da dobim za . zna netko kak sad natjerat da dobim za 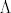 matricu koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule? matricu koja u gonjem lijevom uglu ima jedinicnu matricu reda p,a na ostalim mjestima nule? |
Evo da ja probam, nadam se da neću puno zbrljat.
Dakle, prema mojem skromnom mišljenju, ono prvo ne vrijedi, jer PP' ne mora općenito biti jednako takvoj matrici, ali to ne smeta da se dokaže sve ostalo.
Za drugo, sve svojstvene vrijednosti od P jesu 0 i 1, pa sad samo zamijeniš retke i stupce (valjda) u ovom umnošku matrica. Uglavnom, već smo na linearnoj pokazali da se to može. ne znam sad ovako napamet postupak da "natjeraš" 1 na jednu stranu a 0 na drugu, ali u osnovi smo na linearnoj pokazali da kako su joj samo 0 i 1 svojstvene vrijednosti (i simetrična je) da postoje ovakva ortogonalna matrica koja prevodi P u dijagonalnu sa svojstvenim vrijednostima na dijagonali i naravno tu si možeš narihtat bilo kakav poredak.
Nadam se da je pomoglo 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
johnny
Forumaš(ica)

Pridružen/a: 09. 02. 2005. (14:12:26)
Postovi: (23)16
|
 Postano: 23:53 sub, 31. 1. 2009 Naslov: Postano: 23:53 sub, 31. 1. 2009 Naslov: |
    |
|
|
Evo obecao sam postati jos neka pitanja koja su se pojavljivala na usmenima....
1. M-W-W test - definicija jednostranog testa,u kom smislu je jednostran, sto je F, kriticno podrucje itd.
2. Studentova distribucija
3.x1,x2,x3 nezavisne Bernoullijeve s parametrom p. Izracunati E[x1|x1+x2+x3]
4.ako imamo dva slucajna uzorka duljine n, iz normalne razdiobe i testiramo hiopotezu h0 : mi1=mi2 koju cemo test statistiku koristiti, pa jel bitna nezavisnost, zasto....uglavnom kao i na svakom kolegiju trazi se razumijevanje naucenog.... i to je to :)
Evo obecao sam postati jos neka pitanja koja su se pojavljivala na usmenima....
1. M-W-W test - definicija jednostranog testa,u kom smislu je jednostran, sto je F, kriticno podrucje itd.
2. Studentova distribucija
3.x1,x2,x3 nezavisne Bernoullijeve s parametrom p. Izracunati E[x1|x1+x2+x3]
4.ako imamo dva slucajna uzorka duljine n, iz normalne razdiobe i testiramo hiopotezu h0 : mi1=mi2 koju cemo test statistiku koristiti, pa jel bitna nezavisnost, zasto....uglavnom kao i na svakom kolegiju trazi se razumijevanje naucenog.... i to je to 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|









