|
[latex]I=\int_{0}^{+\infty}\frac{dx}{(4x^2+\pi^2)\mathop{\mathrm{ch}}x}=?[/latex]
Definiramo [latex]f(z)=\frac{1}{(4z^2+\pi^2)\mathop{\mathrm{ch}}z}[/latex]
Funkcija [i]f[/i] ima izolirane singularitete u (nultočkama nazivnika): [latex]\frac{(2k+1)\pi i}{2};\quad k\in\mathbb{Z}[/latex]
Izračunamo reziduume u tim točkama (trebat će nam samo oni u gornjoj poluravnini):
u [latex]\frac{\pi i}{2}[/latex] je pol 2. reda te [latex]\mathop{\mathrm{Res}}(f,\frac{\pi i}{2})=\frac{-i}{4\pi^2}[/latex]
u [latex]\frac{(2k+1)\pi i}{2}[/latex]; k>=1 je pol 1. reda te [latex]\mathop{\mathrm{Res}}(f,\frac{(2k+1)\pi i}{2})=\frac{(-1)^k\, i}{4\pi^2 k(k+1)}[/latex]
Integriramo funkciju [i]f[/i] po (pozitivno orijentiranom) rubu pravokutnika [latex][-R,R]\times [0,k\pi][/latex] (za neke R>0, k€[b]N[/b]).
Dakle, vrhovi pravokutnika su kompleksni brojevi [latex]-R, R, R+k\pi i, -R+k\pi i[/latex]
Prema teoremu o reziduumima taj integral je jednak [latex]2\pi i \sum_{l=0}^{k-1}\mathop{\mathrm{Res}}\left(f,\frac{(2l+1)\pi i}{2}\right)[/latex]
što se može srediti kao [latex]\frac{1}{2\pi}\left(\sum_{l=1}^{k-1}\frac{(-1)^{l-1}}{l}+\sum_{l=1}^{k}\frac{(-1)^{l-1}}{l}\right)[/latex]
Primijetimo da je [latex]\lim_{k\to\infty}[/latex] od posljednjeg izraza jednak [latex]\frac{\ln 2}{\pi}[/latex]
Integrali po stranicama pravokutnika su sljedeći:
-donja stranica: [latex]\int_{-R}^{R}\frac{dx}{(4x^2+\pi^2)\mathop{\mathrm{ch}}x}[/latex]
-gornja stranica: [latex]-\int_{-R}^{R}\frac{dx}{(4(x+k\pi i)^2+\pi^2)\mathop{\mathrm{ch}}x}[/latex]
-desna stranica: [latex]\int_{0}^{k\pi}\frac{i\,dy}{(4(R+y i)^2+\pi^2)\mathop{\mathrm{ch}}(R+y i)}[/latex]
-lijeva stranica: [latex]-\int_{0}^{k\pi}\frac{i\,dy}{(4(-R+y i)^2+\pi^2)\mathop{\mathrm{ch}}(-R+y i)}[/latex]
Najprije ćemo pustiti [latex]\lim_{R\to\infty}[/latex], a zatim [latex]\lim_{k\to\infty}[/latex]
-donja stranica: Integral po donjoj stranici teži prema 2I.
-gornja stranica: Koristeći [latex]\left|4(x+k\pi i)^2+\pi^2\right|\geq (4k^2-1)\pi^2[/latex]
dobivamo da je apsolutno od integrala [latex]\leq\frac{1}{(4k^2-1)\pi^2}\int_{-R}^{R}\frac{dx}{\mathop{\mathrm{ch}}x}[/latex]
Prelaskom na [latex]\lim_{R\to\infty}[/latex] dobivamo [latex]\leq\frac{\pi}{(4k^2-1)\pi^2}[/latex]
a zatim prelaskom na [latex]\lim_{k\to\infty}[/latex] dobijemo 0.
-desna stranica: Koristeći [latex]\left|\mathop{\mathrm{ch}}(R+y i)\right|\geq\mathop{\mathrm{sh}}R[/latex]
te [latex]\left|4(R+y i)^2+\pi^2\right|\geq 4R^2+\pi^2[/latex] (za [latex]R\geq\frac{\pi}{2}[/latex])
dobivamo da je apsolutno od integrala [latex]\leq\frac{k\pi}{(4R^2+\pi^2)\mathop{\mathrm{sh}}R}[/latex]
Prelaskom na [latex]\lim_{R\to\infty}[/latex] dobivamo 0, a zatim prelaskom na [latex]\lim_{k\to\infty}[/latex]
trivijalno opet 0.
-lijeva stranica: Analogno (kao i desna) teži u 0.
Zaključujemo [latex]2I=\frac{\ln 2}{\pi}[/latex], tj. [latex]I=\frac{\ln 2}{2\pi}[/latex]
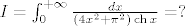
Definiramo 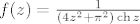
Funkcija f ima izolirane singularitete u (nultočkama nazivnika): 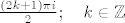
Izračunamo reziduume u tim točkama (trebat će nam samo oni u gornjoj poluravnini):
u 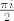 je pol 2. reda te je pol 2. reda te 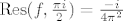
u 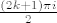 ; k>=1 je pol 1. reda te ; k>=1 je pol 1. reda te 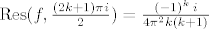
Integriramo funkciju f po (pozitivno orijentiranom) rubu pravokutnika 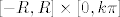 (za neke R>0, k€N). (za neke R>0, k€N).
Dakle, vrhovi pravokutnika su kompleksni brojevi 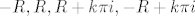
Prema teoremu o reziduumima taj integral je jednak 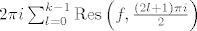
što se može srediti kao 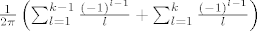
Primijetimo da je 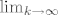 od posljednjeg izraza jednak od posljednjeg izraza jednak 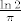
Integrali po stranicama pravokutnika su sljedeći:
-donja stranica: 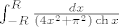
-gornja stranica: 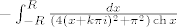
-desna stranica: 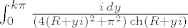
-lijeva stranica: 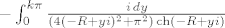
Najprije ćemo pustiti 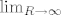 , a zatim , a zatim 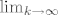
-donja stranica: Integral po donjoj stranici teži prema 2I.
-gornja stranica: Koristeći 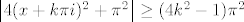
dobivamo da je apsolutno od integrala 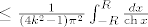
Prelaskom na 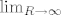 dobivamo dobivamo 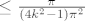
a zatim prelaskom na 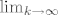 dobijemo 0. dobijemo 0.
-desna stranica: Koristeći 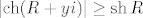
te 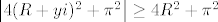 (za (za 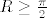 ) )
dobivamo da je apsolutno od integrala 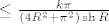
Prelaskom na 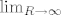 dobivamo 0, a zatim prelaskom na dobivamo 0, a zatim prelaskom na 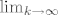
trivijalno opet 0.
-lijeva stranica: Analogno (kao i desna) teži u 0.
Zaključujemo 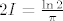 , tj. , tj. 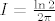
|





