| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 12:59 ned, 12. 11. 2006 Naslov: prostor C^n Postano: 12:59 ned, 12. 11. 2006 Naslov: prostor C^n |
    |
|
|
zanima me radi boljeg shvacanja gradiva kako izgleda baza u C^n(znaci nad kompleksnim poljem C, tj, dimenzija prostora je n) opcenito!
Da li je to mozda [b]{[i]e1[/i], [i]e2[/i], ..., [i]en[/i]}, n element iz N,
[i]e1[/i]=(i,0,0,...,0), ..., [i]en[/i]=(0,0,...,0,i)[/b]?
p.s.ako je ovo baza za C^n sta sam gore napisao onda dolazim do zakljucka da [b]bilokoja baza iz R^n ne moze biti baza i za C^n[/b]!
-->molio bih da netko potvrdi! 8) ( :D )
thnx :)
zanima me radi boljeg shvacanja gradiva kako izgleda baza u C^n(znaci nad kompleksnim poljem C, tj, dimenzija prostora je n) opcenito!
Da li je to mozda {e1, e2, ..., en}, n element iz N,
e1=(i,0,0,...,0), ..., en=(0,0,...,0,i)?
p.s.ako je ovo baza za C^n sta sam gore napisao onda dolazim do zakljucka da bilokoja baza iz R^n ne moze biti baza i za C^n!
→molio bih da netko potvrdi!  ( (  ) )
thnx 
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
 Postano: 13:09 ned, 12. 11. 2006 Naslov: Postano: 13:09 ned, 12. 11. 2006 Naslov: |
    |
|
|
Jedna ortonormirana baza od [latex]\mathbb{C}^n[/latex] nad [latex]\mathbb{C}[/latex] je
[latex]\left\lbrace(1,0,0,\dots,0,0),(0,1,0,\dots,0,0),\dots,(0,0,0,\dots,0,1)\right\rbrace[/latex]
EDIT: I tvoj primjer je baza.
Baza od [latex]\mathbb{C}^n[/latex] nad [latex]\mathbb{R}[/latex] je nesto sasma drugo; dvostruko je veca i -- uzmemo li gornji primjer -- za [latex](0,\dots,0,1,0,\dots,0)[/latex] treba sadrzavati i [latex](0,\dots,0,\imath,0,\dots,0)[/latex].
Jedna ortonormirana baza od 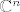 nad nad  je je
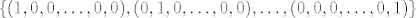
EDIT: I tvoj primjer je baza.
Baza od 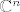 nad nad  je nesto sasma drugo; dvostruko je veca i – uzmemo li gornji primjer – za je nesto sasma drugo; dvostruko je veca i – uzmemo li gornji primjer – za 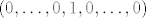 treba sadrzavati i treba sadrzavati i 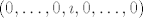 . .
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 13:28 ned, 12. 11. 2006 Naslov: Postano: 13:28 ned, 12. 11. 2006 Naslov: |
    |
|
|
[quote="venovako"]Jedna ortonormirana baza od [latex]\mathbb{C}^n[/latex] nad [latex]\mathbb{C}[/latex] je
[latex]\left\lbrace(1,0,0,\dots,0,0),(0,1,0,\dots,0,0),\dots,(0,0,0,\dots,0,1)\right\rbrace[/latex]
Baza od [latex]\mathbb{C}^n[/latex] nad [latex]\mathbb{R}[/latex] je nesto sasma drugo; dvostruko je veca i -- uzmemo li gornji primjer -- za [latex](0,\dots,0,1,0,\dots,0)[/latex] treba sadrzavati i [latex](0,\dots,0,\imath,0,\dots,0)[/latex].[/quote]
meni sad nije jasno kako je ovo sto si ti napisao baza za C^n :?: ..pa zar ne znaci ako je C^n prostor nad kompleksnim poljem C da MORA imati kompleksne koeficijente(a ja ih nigdje ne vidim.. :oops: )
ILI se moram drzati ko pijan plota one "stare" :lol: da ako je skup lin. nez. i broj elemenata mu je jednak dim prostora (u ovom slucaju n=n, dim C^n=n) da je onda baza za taj prostor!?!? :idea:
ufff, nikako mi ne ide u ovome svemu u glavu cinjenica da je nesto kompleksno(vekt. prostor) iznad neceg kompleksnog(polja) a da kao rezultat (npr baza) nema veze sa komplesknim koeficijentima.... :? :roll:
| venovako (napisa): | Jedna ortonormirana baza od 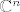 nad nad  je je
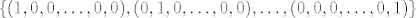
Baza od 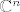 nad nad  je nesto sasma drugo; dvostruko je veca i – uzmemo li gornji primjer – za je nesto sasma drugo; dvostruko je veca i – uzmemo li gornji primjer – za 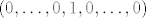 treba sadrzavati i treba sadrzavati i 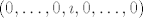 . . |
meni sad nije jasno kako je ovo sto si ti napisao baza za C^n  ..pa zar ne znaci ako je C^n prostor nad kompleksnim poljem C da MORA imati kompleksne koeficijente(a ja ih nigdje ne vidim.. ..pa zar ne znaci ako je C^n prostor nad kompleksnim poljem C da MORA imati kompleksne koeficijente(a ja ih nigdje ne vidim..  ) )
ILI se moram drzati ko pijan plota one "stare"  da ako je skup lin. nez. i broj elemenata mu je jednak dim prostora (u ovom slucaju n=n, dim C^n=n) da je onda baza za taj prostor!?!? da ako je skup lin. nez. i broj elemenata mu je jednak dim prostora (u ovom slucaju n=n, dim C^n=n) da je onda baza za taj prostor!?!? 
ufff, nikako mi ne ide u ovome svemu u glavu cinjenica da je nesto kompleksno(vekt. prostor) iznad neceg kompleksnog(polja) a da kao rezultat (npr baza) nema veze sa komplesknim koeficijentima....  
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 13:33 ned, 12. 11. 2006 Naslov: Postano: 13:33 ned, 12. 11. 2006 Naslov: |
    |
|
|
[quote="venovako"]...
EDIT: I tvoj primjer je baza.
...
[/quote]
ponukan time :) , daj onda reci dal to znaci da je onda lin nez skup u R^n isto lin nez i u C^n!?
i ako je taj isti skup (npr {a1, ..., ak}) baza za R^n onda je i baza za C^n....
(mislim ako je lin nez, a po tvome jest, i ima jednak broj elemenata kao i dim prostora -->>onda je i BAZA) :idea: :twisted:
| venovako (napisa): | ...
EDIT: I tvoj primjer je baza.
...
|
ponukan time  , daj onda reci dal to znaci da je onda lin nez skup u R^n isto lin nez i u C^n!? , daj onda reci dal to znaci da je onda lin nez skup u R^n isto lin nez i u C^n!?
i ako je taj isti skup (npr {a1, ..., ak}) baza za R^n onda je i baza za C^n....
(mislim ako je lin nez, a po tvome jest, i ima jednak broj elemenata kao i dim prostora →>onda je i BAZA)  
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
 Postano: 14:51 ned, 12. 11. 2006 Naslov: Postano: 14:51 ned, 12. 11. 2006 Naslov: |
    |
|
|
[quote="13_mac"]ponukan time :) , daj onda reci dal to znaci da je onda lin nez skup u R^n isto lin nez i u C^n!?[/quote]
Linearno nezavisan skup u [latex]\mathbb{R}^n[/latex] nezavisan je obzirom na lin. kombinaciju s realnim koeficijentima... uzmimo da taj skup ima [latex]n[/latex] elemenata, onda:
[latex]\mathsf{A}:\quad\displaystyle\sum_{i=1}^n\lambda_i\,r_i=0\Rightarrow(\forall\,i)\lambda_i=0[/latex]
gdje su [latex]\lambda_i\in\mathbb{R},r_i\in\mathbb{R}^n[/latex]
Shvatimo li realne vektore kao kompleksne s imaginarnim dijelom jednakim 0 i promatramo li ih u kontekstu kompleksnog vektorskog prostora, pogledajmo kad je zadovoljena lin. kombinacija:
[latex]\mathsf{B}:\quad\displaystyle\sum_{i=1}^n\mu_i\,r_i=0[/latex]
gdje su [latex]\mu_i\in\mathbb{C}[/latex].
Kad bi svi [latex]\mu_i[/latex] imali imaginarni dio jednak 0, onda bismo bili u slucaju A, pa bi vrijedilo [latex](\forall\,i)\mu_i=0[/latex].
Neka postoji [latex]j[/latex] t.d. [latex]\mu_j[/latex] ima netrivijalan imaginarni dio. Kako su komponente od [latex]r_j[/latex] realne, to vrijedi:
[latex]\mu_j\,r_j=\Re(\mu_j)\,r_j+\imath\,\Im(\mu_j)\,r_j[/latex]
Stovise, neka postoji [latex]k\ge 1[/latex] takvih [latex]j[/latex]-tova.
Ubacimo to u B:
[latex]\displaystyle\sum_{\left\lbrace i:1\le i\le n\right\rbrace\backslash\left\lbrace j_1,\dots,j_k\right\rbrace}\mu_i\,r_i+\sum_{l=1}^k\Re(\mu_{j_l})\,r_{j_l}=-\imath\,\sum_{l=1}^k\Im(\mu_{j_l})\,r_{j_l}[/latex]
Lijeva strana jednakosti je realni, a desna imaginarni vektor.
To je moguce samo ako su obje strane nul-vektori.
Iz toga i A slijedi:
[latex](\forall\,l)1\le l\le k\Rightarrow\Re(\mu_{j_l})=0[/latex]
te [latex]\mu_i=0[/latex] za preostale [latex]\mu_i[/latex].
Sad se sjetimo da je podskup lin. nezavisnog skupa takodjer lin. nezavisan.
Iz toga i cinjenice da je suma ([i]bez[/i] [latex]\imath[/latex]) na desnoj strani realni nul-vektor dobivamo:
[latex](\forall\,l)1\le l\le k\Rightarrow\Im(\mu_{j_l})=0[/latex].
Gornja dva rezultata skupa daju:
[latex](\forall\,i)1\le i\le n\Rightarrow\mu_i=0[/latex]
pa je [latex]\left\lbrace r_i:1\le i\le n\right\rbrace[/latex], promatran kao skup kompleksnih vektora u kompleksnom vekt. prostoru, takodjer linearno nezavisan ;)
| 13_mac (napisa): | ponukan time  , daj onda reci dal to znaci da je onda lin nez skup u R^n isto lin nez i u C^n!? , daj onda reci dal to znaci da je onda lin nez skup u R^n isto lin nez i u C^n!? |
Linearno nezavisan skup u  nezavisan je obzirom na lin. kombinaciju s realnim koeficijentima... uzmimo da taj skup ima nezavisan je obzirom na lin. kombinaciju s realnim koeficijentima... uzmimo da taj skup ima  elemenata, onda: elemenata, onda:
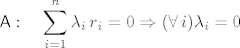
gdje su 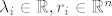
Shvatimo li realne vektore kao kompleksne s imaginarnim dijelom jednakim 0 i promatramo li ih u kontekstu kompleksnog vektorskog prostora, pogledajmo kad je zadovoljena lin. kombinacija:
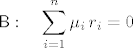
gdje su 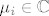 . .
Kad bi svi 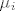 imali imaginarni dio jednak 0, onda bismo bili u slucaju A, pa bi vrijedilo imali imaginarni dio jednak 0, onda bismo bili u slucaju A, pa bi vrijedilo 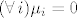 . .
Neka postoji 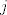 t.d. t.d. 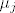 ima netrivijalan imaginarni dio. Kako su komponente od ima netrivijalan imaginarni dio. Kako su komponente od 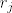 realne, to vrijedi: realne, to vrijedi:
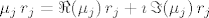
Stovise, neka postoji  takvih takvih 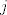 -tova. -tova.
Ubacimo to u B:
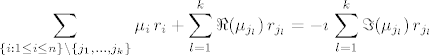
Lijeva strana jednakosti je realni, a desna imaginarni vektor.
To je moguce samo ako su obje strane nul-vektori.
Iz toga i A slijedi:
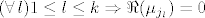
te 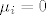 za preostale za preostale 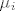 . .
Sad se sjetimo da je podskup lin. nezavisnog skupa takodjer lin. nezavisan.
Iz toga i cinjenice da je suma (bez  ) na desnoj strani realni nul-vektor dobivamo: ) na desnoj strani realni nul-vektor dobivamo:
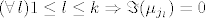 . .
Gornja dva rezultata skupa daju:
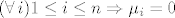
pa je 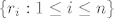 , promatran kao skup kompleksnih vektora u kompleksnom vekt. prostoru, takodjer linearno nezavisan , promatran kao skup kompleksnih vektora u kompleksnom vekt. prostoru, takodjer linearno nezavisan 
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
|









