| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
dosed_girl
Forumaš(ica)

Pridružen/a: 04. 12. 2006. (21:01:46)
Postovi: (6F)16
Spol: 
Lokacija: -zG-
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 0:21 pon, 18. 6. 2007 Naslov: Postano: 0:21 pon, 18. 6. 2007 Naslov: |
    |
|
|
[quote="ma"]eh. baš dobro da postoji tema za eventualne nejasnoće oko skripte. :?
mene muče oni integrali na stranici 172. s prva tri se slažem, ali rekao bih da su i ostala dva jednaka 0. ako raspišemo te funkcije pomoću adicijskih formula dobijemo (pokazat ću samo prvi):
[latex]\int_{-\pi}^{\pi} sin(nx) sin(mx) dx = \frac{1}{2}(\int_{-\pi}^{\pi}cos[(n-m)x] dx - \int_{-\pi}^{\pi}cos[(n+m)x] dx) =[/latex]
[latex]= \frac{1}{2}(\frac{sin[(n-m)x]}{n-m} |_{-\pi}^{\pi} - \frac{sin[(n+m)x]}{n+m} |_{-\pi}^{\pi})[/latex].
kako je sin(k[latex]\pi[/latex]) = 0, za svako k[latex]\in[/latex] Z, gornji je integral jednak 0 neovisno o m i n.
gdje mi je greška? :neznam:[/quote]
ma valjda to što dijeliš sa n-m, a to se baš i ne smije ako je n=m... a za n=m dobiješ ono što je matmih napisao :) inače je 0, ako su n i m različiti... pa je u skripti, čini mi se, sve ok što se toga tiče... valjda :)
edit: eh, da, vidim sad da me shimija pretekao :)
| ma (napisa): | eh. baš dobro da postoji tema za eventualne nejasnoće oko skripte. 
mene muče oni integrali na stranici 172. s prva tri se slažem, ali rekao bih da su i ostala dva jednaka 0. ako raspišemo te funkcije pomoću adicijskih formula dobijemo (pokazat ću samo prvi):
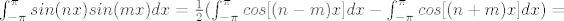
 . .
kako je sin(k ) = 0, za svako k ) = 0, za svako k Z, gornji je integral jednak 0 neovisno o m i n. Z, gornji je integral jednak 0 neovisno o m i n.
gdje mi je greška?  |
ma valjda to što dijeliš sa n-m, a to se baš i ne smije ako je n=m... a za n=m dobiješ ono što je matmih napisao  inače je 0, ako su n i m različiti... pa je u skripti, čini mi se, sve ok što se toga tiče... valjda inače je 0, ako su n i m različiti... pa je u skripti, čini mi se, sve ok što se toga tiče... valjda 
edit: eh, da, vidim sad da me shimija pretekao 
_________________ kalendar 
  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
MKova
Forumaš(ica)

Pridružen/a: 01. 10. 2005. (18:24:38)
Postovi: (187)16
Spol: 
|
 Postano: 17:15 sub, 23. 6. 2007 Naslov: Postano: 17:15 sub, 23. 6. 2007 Naslov: |
    |
|
|
može li mi tko objasniti što znači ovo? :)
strana 128., propozicija 5.1.
Ako [latex]h:[a,b] \rightarrow \mathbb{R}[/latex] isčezava svugdje osim možda u točki [latex]c\in[a,b][/latex], onda je [latex]h[/latex] integrabilna na [latex][a,b][/latex] i [latex]\int^a_bf(x)dx=0[/latex]
Što znači kad funkcija isčezava?
Dalje, što znači kada funkcija ima konačno mnogo prekida prve vrste? Kužim da je to prekid prekid prve vrste tako da f(x) postoji, samo da ne zadovoljava neprekidnost tj. limes funkcije u c nije jednak f(c), ima li još nešto što bi trebao znati?
Hvala, bit će još pitanja :)
može li mi tko objasniti što znači ovo? 
strana 128., propozicija 5.1.
Ako 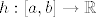 isčezava svugdje osim možda u točki isčezava svugdje osim možda u točki 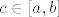 , onda je , onda je 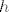 integrabilna na integrabilna na 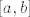 i i 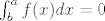
Što znači kad funkcija isčezava?
Dalje, što znači kada funkcija ima konačno mnogo prekida prve vrste? Kužim da je to prekid prekid prve vrste tako da f(x) postoji, samo da ne zadovoljava neprekidnost tj. limes funkcije u c nije jednak f(c), ima li još nešto što bi trebao znati?
Hvala, bit će još pitanja 
_________________ suradnici za razvoj igre traženi!! vidi ovo |
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 18:11 sub, 23. 6. 2007 Naslov: Postano: 18:11 sub, 23. 6. 2007 Naslov: |
    |
|
|
[quote="MKova"]
Ako [latex]h:[a,b] \rightarrow \mathbb{R}[/latex] isčezava svugdje osim možda u točki [latex]c\in[a,b][/latex], onda je [latex]h[/latex] integrabilna na [latex][a,b][/latex] i [latex]\int^a_b h(x)dx=0[/latex]
Što znači kad funkcija isčezava?[/quote]
Da je skoro svuda jednaka nuli tj. osim eventualno na skupu mjere nula( premda ne bih htio ulaziti u to sta to znaci -skoro svuda- , treba znati malo teorije mjere)
[quote="MKova"]
Dalje, što znači kada funkcija ima konačno mnogo prekida prve vrste? Kužim da je to prekid prekid prve vrste tako da f(x) postoji, samo da ne zadovoljava neprekidnost tj. limes funkcije u c nije jednak f(c), ima li još nešto što bi trebao znati?
Hvala, bit će još pitanja :)[/quote]
Upravo to sto si napisao,dakle ima konacno mnogo tocaka u kojima fija nije neprekidna.
| MKova (napisa): |
Ako 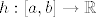 isčezava svugdje osim možda u točki isčezava svugdje osim možda u točki 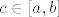 , onda je , onda je 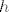 integrabilna na integrabilna na 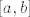 i i 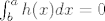
Što znači kad funkcija isčezava? |
Da je skoro svuda jednaka nuli tj. osim eventualno na skupu mjere nula( premda ne bih htio ulaziti u to sta to znaci -skoro svuda- , treba znati malo teorije mjere)
| MKova (napisa): |
Dalje, što znači kada funkcija ima konačno mnogo prekida prve vrste? Kužim da je to prekid prekid prve vrste tako da f(x) postoji, samo da ne zadovoljava neprekidnost tj. limes funkcije u c nije jednak f(c), ima li još nešto što bi trebao znati?
Hvala, bit će još pitanja  |
Upravo to sto si napisao,dakle ima konacno mnogo tocaka u kojima fija nije neprekidna.
|
|
| [Vrh] |
|
|














