| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vlado
Gost
|
|
| [Vrh] |
|
Vlado
Gost
|
|
| [Vrh] |
|
Vlado
Gost
|
|
| [Vrh] |
|
Vlado
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 14:34 čet, 8. 3. 2007 Naslov: Postano: 14:34 čet, 8. 3. 2007 Naslov: |
    |
|
|
[quote="Vlado"]Rjesio sam konvergenciju sume za 1.
Ukoliko nisam nesto previdio ,konvergira po Cauchyevom kriteriju :
[latex]|a_{n+1}-a_{n}|<\epsilon[/latex]
(ako nisam nesto previdio :))
To znaci :
[latex]\displaystyle\prod_{n=1}^{\infty}(cos\frac{1}{n})>0[/latex][/quote]
Kako si iz "konvergira po <nekom> kriteriju" dosao do "to cemu konvergira je strogo vece od nule"? :-k Zar ne moze konvergirati u nulu? :-k
Dodatno, ne odnosi li se Cauchyjev kriterij na [b]sume[/b]? :-k Ti imas produkt. :|
Ovo ocito konvergira jer parcijalne sume cine ogranicen strogo monoton niz (niz je padajuci, a sve vrijednosti su izmedju cos 1 i 0). 8) Pitanje je samo kovergira li u nulu ili nesto strogo pozitivno. :)
Sorry, ne sjecam se tih stoseva dovoljno da rijesim na brzinu, a malo sam u zurbi, pa ne stignem mozgati. :|
| Vlado (napisa): | Rjesio sam konvergenciju sume za 1.
Ukoliko nisam nesto previdio ,konvergira po Cauchyevom kriteriju :
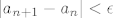
(ako nisam nesto previdio  ) )
To znaci :
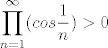 |
Kako si iz "konvergira po <nekom> kriteriju" dosao do "to cemu konvergira je strogo vece od nule"?  Zar ne moze konvergirati u nulu? Zar ne moze konvergirati u nulu? 
Dodatno, ne odnosi li se Cauchyjev kriterij na sume?  Ti imas produkt. Ti imas produkt. 
Ovo ocito konvergira jer parcijalne sume cine ogranicen strogo monoton niz (niz je padajuci, a sve vrijednosti su izmedju cos 1 i 0).  Pitanje je samo kovergira li u nulu ili nesto strogo pozitivno. Pitanje je samo kovergira li u nulu ili nesto strogo pozitivno. 
Sorry, ne sjecam se tih stoseva dovoljno da rijesim na brzinu, a malo sam u zurbi, pa ne stignem mozgati. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 21:11 čet, 8. 3. 2007 Naslov: Re: Beskonacni produkti Postano: 21:11 čet, 8. 3. 2007 Naslov: Re: Beskonacni produkti |
    |
|
|
[quote="Vlado"]Imam dva zadatka iz ruske zbirke koje ne mogu rijesiti.
[latex]1[/latex]
Da li je :
[latex]\displaystyle\prod_{n=1}^{\infty} cos(\frac{1}{n})>0[/latex]
Ili je mozda ipak u limesu=0?
[/quote]
[latex]\displaystyle \prod_{n=1}^{\infty}\cos(\frac{1}{n}) [/latex] je octio [latex]>0[/latex] i to iz jednostavnog razloga. Da bi taj produkt bio jednak nuli moram (barem) jedan clan biti jednak 0 , a takav u tvojem produktu ne postoji. Pogledas prvi clan [latex]\displaystyle \cos(\frac{1}{1})\neq 0 [/latex] ,a [latex]\displaystyle \cos (x) \neq 0 , \forall x\in [0,\frac{\pi}{2}>[/latex] ,pa onda specijalno , [latex]\displaystyle \cos(\frac{1}{n})\neq 0 , \forall n\in \mathbb{N}[/latex]. Da bi izracuali koliko je tocno produkt,treba se malo namuciti :wink: .
Edit: isti argument upotrijebi da bi nasao x u drugom zadatku
| Vlado (napisa): | Imam dva zadatka iz ruske zbirke koje ne mogu rijesiti.

Da li je :
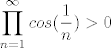
Ili je mozda ipak u limesu=0?
|
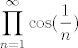 je octio je octio 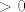 i to iz jednostavnog razloga. Da bi taj produkt bio jednak nuli moram (barem) jedan clan biti jednak 0 , a takav u tvojem produktu ne postoji. Pogledas prvi clan i to iz jednostavnog razloga. Da bi taj produkt bio jednak nuli moram (barem) jedan clan biti jednak 0 , a takav u tvojem produktu ne postoji. Pogledas prvi clan 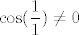 ,a ,a 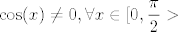 ,pa onda specijalno , ,pa onda specijalno , 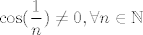 . Da bi izracuali koliko je tocno produkt,treba se malo namuciti . Da bi izracuali koliko je tocno produkt,treba se malo namuciti  . .
Edit: isti argument upotrijebi da bi nasao x u drugom zadatku
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Vlado
Gost
|
 Postano: 13:54 pet, 9. 3. 2007 Naslov: Postano: 13:54 pet, 9. 3. 2007 Naslov: |
    |
|
|
[quote="vsego"][quote="Vlado"]Rjesio sam konvergenciju sume za 1.
Ukoliko nisam nesto previdio ,konvergira po Cauchyevom kriteriju :
[latex]|a_{n+1}-a_{n}|<\epsilon[/latex]
(ako nisam nesto previdio :))
To znaci :
[latex]\displaystyle\prod_{n=1}^{\infty}(cos\frac{1}{n})>0[/latex][/quote]
Kako si iz "konvergira po <nekom> kriteriju" dosao do "to cemu konvergira je strogo vece od nule"? :-k Zar ne moze konvergirati u nulu? :-k
Dodatno, ne odnosi li se Cauchyjev kriterij na [b]sume[/b]? :-k Ti imas produkt. :|
Ovo ocito konvergira jer parcijalne sume cine ogranicen strogo monoton niz (niz je padajuci, a sve vrijednosti su izmedju cos 1 i 0). 8) Pitanje je samo kovergira li u nulu ili nesto strogo pozitivno. :)
|[/quote]
Ako je :
[latex]\displaystyle\prod_{n=1}^{\infty}a_{n}=0[/latex]
Tada je [u]po definiciji[/u] produkt divergentan.
To je mozda cudna formulacija,ali tako pise u mojoj knjizi!
Da bi beskonacan product bio konvergentan mora mu limes biti
a)Konacan
b)Razlicit od nule.
Glupi razlog je valjda:
Ispitivanje konvergencije beskonacnog produkta je ekvivalentno ispitivanju konvergencije reda:
[latex]\sum_{n=1}^{\infty}log(a_{n}) [/latex]
Ako taj red konvergira sigurno konvergira i produkt.
Sad pitanje za IQ80:Sta se zbiva kad pod znakom logaritma imamo 0 :?: :D
Mr Doe:[i]
"Da bi taj produkt bio jednak nuli moram (barem) jedan clan biti jednak 0 , a takav u tvojem produktu ne postoji."[/i]
Sorry ,ali slazem se sa vsegom da je ovo glupost.Po tome bi bilo
[latex]\displaystyle\prod_{n=1}^{\infty}\frac{1}{n}> 0[/latex]
Jer nijedan clan u produktu nije jednak 0.
vsego:cekam pomoc za drugi.
Glupi Ferovac[/i]
| vsego (napisa): | | Vlado (napisa): | Rjesio sam konvergenciju sume za 1.
Ukoliko nisam nesto previdio ,konvergira po Cauchyevom kriteriju :
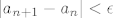
(ako nisam nesto previdio  ) )
To znaci :
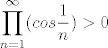 |
Kako si iz "konvergira po <nekom> kriteriju" dosao do "to cemu konvergira je strogo vece od nule"?  Zar ne moze konvergirati u nulu? Zar ne moze konvergirati u nulu? 
Dodatno, ne odnosi li se Cauchyjev kriterij na sume?  Ti imas produkt. Ti imas produkt. 
Ovo ocito konvergira jer parcijalne sume cine ogranicen strogo monoton niz (niz je padajuci, a sve vrijednosti su izmedju cos 1 i 0).  Pitanje je samo kovergira li u nulu ili nesto strogo pozitivno. Pitanje je samo kovergira li u nulu ili nesto strogo pozitivno. 
| |
Ako je :
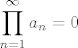
Tada je po definiciji produkt divergentan.
To je mozda cudna formulacija,ali tako pise u mojoj knjizi!
Da bi beskonacan product bio konvergentan mora mu limes biti
a)Konacan
b)Razlicit od nule.
Glupi razlog je valjda:
Ispitivanje konvergencije beskonacnog produkta je ekvivalentno ispitivanju konvergencije reda:
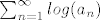
Ako taj red konvergira sigurno konvergira i produkt.
Sad pitanje za IQ80:Sta se zbiva kad pod znakom logaritma imamo 0  
Mr Doe:
"Da bi taj produkt bio jednak nuli moram (barem) jedan clan biti jednak 0 , a takav u tvojem produktu ne postoji."
Sorry ,ali slazem se sa vsegom da je ovo glupost.Po tome bi bilo
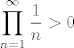
Jer nijedan clan u produktu nije jednak 0.
vsego:cekam pomoc za drugi.
Glupi Ferovac[/i]
|
|
| [Vrh] |
|
Vlado
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 14:55 čet, 15. 3. 2007 Naslov: Postano: 14:55 čet, 15. 3. 2007 Naslov: |
    |
|
|
[quote]
Sorry ,ali slazem se sa vsegom da je ovo glupost.Po tome bi bilo
[latex]\displaystyle\prod_{n=1}^{\infty}\frac{1}{n}> 0[/latex]
Jer nijedan clan u produktu nije jednak 0.
Glupi Ferovac[/i][/quote]
Imas prvo ovo apsolutno nije tocno (ovo sam nabrzinu "ispalio" :oops: ).
Pogledajmo kako bi to generalno napravili, promatramo [latex] \prod (1+a_n) [/latex] (gdje je [latex]a_n[/latex] niz,koji zbog jednostvnosti ima konstantan (ili eventualno konstantan ) predznak ) , tada produkt konvegira akko niz [latex]\sum a_n [/latex] konvergira. U tvojem slucaju jest [latex]\cos(\frac{1}{n})=1-\frac{1}{2n^2}+O(n^{-4}) [/latex] . Mozes provjeriti,limes mu je otprilike [latex]0.388356[/latex] ,no ne znam kako bi eksplicitno nasao limes. :cry:
Gosti:Smirimo malo tenzije,nemaju ljudi vremena stalno visiti po forumu. 8)
| Citat: |
Sorry ,ali slazem se sa vsegom da je ovo glupost.Po tome bi bilo
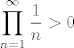
Jer nijedan clan u produktu nije jednak 0.
Glupi Ferovac[/i] |
Imas prvo ovo apsolutno nije tocno (ovo sam nabrzinu "ispalio"  ). ).
Pogledajmo kako bi to generalno napravili, promatramo 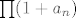 (gdje je (gdje je 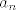 niz,koji zbog jednostvnosti ima konstantan (ili eventualno konstantan ) predznak ) , tada produkt konvegira akko niz niz,koji zbog jednostvnosti ima konstantan (ili eventualno konstantan ) predznak ) , tada produkt konvegira akko niz 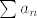 konvergira. U tvojem slucaju jest konvergira. U tvojem slucaju jest 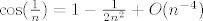 . Mozes provjeriti,limes mu je otprilike . Mozes provjeriti,limes mu je otprilike 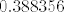 ,no ne znam kako bi eksplicitno nasao limes. ,no ne znam kako bi eksplicitno nasao limes. 
Gosti:Smirimo malo tenzije,nemaju ljudi vremena stalno visiti po forumu. 
|
|
| [Vrh] |
|
|






