|
Pozdrav, imam pitanje u vezi jednog zadatka s prijemnog;
trebalo je odrediti vrijednost sljedeće sume:
[latex]\frac{1}{2 \cdot 6} + \frac{1}{6 \cdot 10} + \frac{1}{10 \cdot 14} + \cdots + \frac{1}{2002 \cdot 2006}[/latex]
Evo kako sam to pokušao riješiti, vrlo vjerojatno postoji i neki elegantniji način...
Prvo sam gornji izraz raspisao ovako:
[latex]\frac{1}{(2+0) \cdot (2+4)} + \frac{1}{(2+4) \cdot (2+8)} + \frac{1}{(2+8) \cdot (2+12)} + \cdots [/latex]
Iz čega slijedi izraz za "opći član"
[latex]a_n=\frac{1}{[2+(n-1) \cdot 4] \cdot (2+n \cdot 4)} [/latex]
Provjera za, recimo, [latex]n=3[/latex]
[latex]a_3=\frac{1}{(2+2 \cdot 4) \cdot (2+3 \cdot 4)}=\frac{1}{10 \cdot 14} [/latex]
Kad se sredi, izraz za opći član izgleda ovako:
[latex]a_n=\frac{1}{4 \cdot (4n^{2}-1)} [/latex]
te is toga izravno za zadnji zadani član slijedi:
[latex]\frac{1}{2002 \cdot 2006}=a_{501} [/latex]
i da bi se odredila vrijednost zadane sume, jednostavno treba zbrojiti sve članove od [latex]n=1[/latex] do [latex]n=501[/latex]:
[latex]\sum_{n=1}^{501} \frac{1}{4 \cdot (4n^{2}-1)} [/latex] odnosno [latex]\frac{1}{4} \sum_{n=1}^{501} \frac{1}{4n^{2}-1} [/latex]
I pitanje je, naravno, kako dalje! Kako preobličiti gornji izraz da se može odrediti njegova suma, jer da je ovo suma geometrijskog niza primijenila bi se formula [latex]S_n=a_1 \frac{q^{n}-1}{q-1}[/latex], no treba znati kvocijent [latex](q)[/latex]. Opet, kad bi se radilo o sumi aritmetičkog niza, suma bi se dobila iz [latex]S_n= \frac{n(a_1+a_n)}{2}[/latex], no opet treba biti poznata diferencija [latex](d)[/latex]. Pitanje je koliko je to uopće relevantno za gore zadanu sumu.
Kada sam gornji izraz ubacio u Mathematicu, izbacila je točno rješenje:
[latex]\frac{1}{4} \sum_{n=1}^{501} \frac{1}{4n^{2}-1} = \frac{501}{4012} [/latex]
No, naravno, na prijemnom nije bilo Mathematice. :wink:
Pozdrav, imam pitanje u vezi jednog zadatka s prijemnog;
trebalo je odrediti vrijednost sljedeće sume:
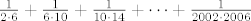
Evo kako sam to pokušao riješiti, vrlo vjerojatno postoji i neki elegantniji način...
Prvo sam gornji izraz raspisao ovako:
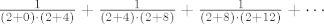
Iz čega slijedi izraz za "opći član"
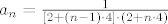
Provjera za, recimo, 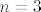
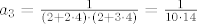
Kad se sredi, izraz za opći član izgleda ovako:
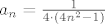
te is toga izravno za zadnji zadani član slijedi:
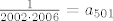
i da bi se odredila vrijednost zadane sume, jednostavno treba zbrojiti sve članove od 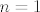 do do 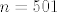 : :
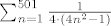 odnosno odnosno 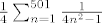
I pitanje je, naravno, kako dalje! Kako preobličiti gornji izraz da se može odrediti njegova suma, jer da je ovo suma geometrijskog niza primijenila bi se formula 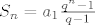 , no treba znati kvocijent , no treba znati kvocijent 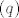 . Opet, kad bi se radilo o sumi aritmetičkog niza, suma bi se dobila iz . Opet, kad bi se radilo o sumi aritmetičkog niza, suma bi se dobila iz 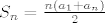 , no opet treba biti poznata diferencija , no opet treba biti poznata diferencija 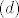 . Pitanje je koliko je to uopće relevantno za gore zadanu sumu. . Pitanje je koliko je to uopće relevantno za gore zadanu sumu.
Kada sam gornji izraz ubacio u Mathematicu, izbacila je točno rješenje:
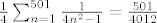
No, naravno, na prijemnom nije bilo Mathematice. 
|




