RP2 - Predavanje 4
Izvor: KiWi
(→Funkcije zadane pomoću integrala) |
|||
| (Nije prikazano 18 međuinačica) | |||
| Redak 10: | Redak 10: | ||
Provjerite koliko se ovako izračunata približna vrijednost derivacije razlikuje od stvarne vrijednosti derivacije. Ispitajte za funkcije <math>sin(x)</math> i <math>x^5</math> | Provjerite koliko se ovako izračunata približna vrijednost derivacije razlikuje od stvarne vrijednosti derivacije. Ispitajte za funkcije <math>sin(x)</math> i <math>x^5</math> | ||
| + | |||
| + | === Zadatak === | ||
| + | Odredite približnu vrijednost derivacije funkcije <math>f(x)=\frac{x^3-1}{2x+7}</math> za razne vrijednosti <math>\big. h</math> i usporedite sa stvarnom vrijednošću derivacije ove funkcije koju ste odredili pomoću sustava Wolfram Alpha | ||
== Integral == | == Integral == | ||
| Redak 22: | Redak 25: | ||
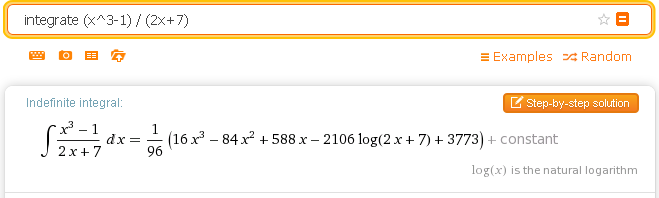
* <math>f(x)=\frac{x^3-1}{2x+7}</math> | * <math>f(x)=\frac{x^3-1}{2x+7}</math> | ||
| + | |||
| + | * [[Datoteka:integral.png]] | ||
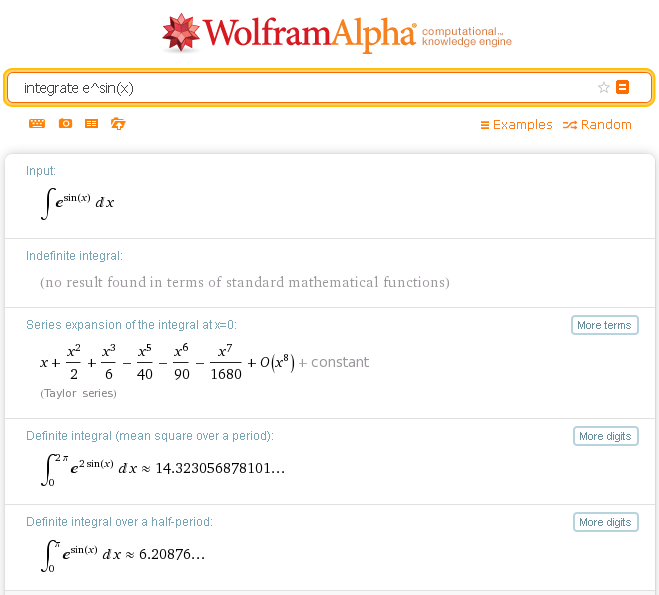
* <math>\ f(x)=e^{\sin x}</math> | * <math>\ f(x)=e^{\sin x}</math> | ||
| + | |||
| + | * [[Datoteka:integral2.png|659px]] | ||
* <math>\ f(x)=a \sin (b x)</math> | * <math>\ f(x)=a \sin (b x)</math> | ||
Za sve ove funkcije odredite vrijednost neodređenog i određenog integrala koristeći sustav Wolfram Alpha. Usporedite vrijednosti dobivene numeričkom metodom i stvarne vrijednosti | Za sve ove funkcije odredite vrijednost neodređenog i određenog integrala koristeći sustav Wolfram Alpha. Usporedite vrijednosti dobivene numeričkom metodom i stvarne vrijednosti | ||
| - | |||
== Simpsonova formula za računanje integrala == | == Simpsonova formula za računanje integrala == | ||
| Redak 40: | Redak 46: | ||
pri čemu je <math>\ x_i=a+ih</math> za <math>\ i=0, 1, ..., n-1, n</math>, uz <math>h=(b-a)/n</math>; Posebno, <math>x_0=a</math> and <math>x_n=b</math>. Gornja formula se može pisati i kao | pri čemu je <math>\ x_i=a+ih</math> za <math>\ i=0, 1, ..., n-1, n</math>, uz <math>h=(b-a)/n</math>; Posebno, <math>x_0=a</math> and <math>x_n=b</math>. Gornja formula se može pisati i kao | ||
| - | <math>\int_a^b f(x) \, dx\approx | + | <math> |
| - | \tfrac{h}{3}\bigg[f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+\cdots+4f(x_{n-1})+f(x_n)\bigg] | + | \begin{align} |
| - | =\tfrac{h}{3}\sum_{i=1}^{n/2}\bigg[f(x_{2i-2})+4f(x_{2i-1})+f(x_{2i})\bigg].</math> | + | \int_a^b f(x) \, dx & \approx |
| + | \tfrac{h}{3}\bigg[f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+\cdots+4f(x_{n-1})+f(x_n)\bigg] = \\ | ||
| + | & = \tfrac{h}{3}\sum_{i=1}^{n/2}\bigg[f(x_{2i-2})+4f(x_{2i-1})+f(x_{2i})\bigg].\\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | |||
=== Funkcije zadane pomoću integrala === | === Funkcije zadane pomoću integrala === | ||
| - | Neke se funkcije zadaju pomoću integrale drugih funkcija. Odnosno, ako je na segmentu <math>\ | + | Neke se funkcije zadaju pomoću integrale drugih funkcija. Odnosno, ako je na segmentu <math>\big[a,b\big]</math> zadana integrabilna funkcija <math>f(x)</math>, onda možemo definirati funkciju |
<math>F(x)=\int_a^x f(t)\, dt</math> | <math>F(x)=\int_a^x f(t)\, dt</math> | ||
| - | Izračunajte na ovaj način (približno pomoću Excela i toćno uvrštavanjem vrijednosti integrala funkcije f) vrijednosti funkcije <math>\int_0^x \frac{t^3-1}{2t+7} \, dt</math> u 101 točki iz intervala <math>\[a,b\]</math>. | + | Izračunajte na ovaj način (približno pomoću Excela i toćno uvrštavanjem vrijednosti integrala funkcije f) vrijednosti funkcije <math>\int_0^x \frac{t^3-1}{2t+7} \, dt</math> u 101 točki iz intervala <math>\big[a,b\big]</math>. |
Nacrtajte graf obje funkcije. | Nacrtajte graf obje funkcije. | ||
| + | |||
| + | == Excel datoteka uz predavanja == | ||
| + | |||
| + | [[Datoteka:Predavanja4_201503261145.zip]] | ||
== Euklidov algoritam == | == Euklidov algoritam == | ||
Za domaću zadaću napraviti radni list na kojem se računa najveća zajednička mjera dvaju brojeva [http://en.wikipedia.org/wiki/Euclidean_algorithm Euklidovim algoritmom] | Za domaću zadaću napraviti radni list na kojem se računa najveća zajednička mjera dvaju brojeva [http://en.wikipedia.org/wiki/Euclidean_algorithm Euklidovim algoritmom] | ||
Trenutačna izmjena od 14:40, 26. ožujka 2015.
Sadržaj |
Derivacija
Derivacija funkcije u točki x0 definira se kao
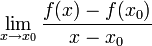
Približna vrijednost derivacije može se odrediti tako da se za dani h > 0 računa
kvocijent diferencija 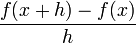 .
.
Napravite u Excelu tablicu koja će za dani h > 0 računati 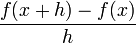 (za sve vrijednosti argumenta iz nekog zadanog skupa). Zadaje se granice intervala na kojem se računa, broj točaka u kojima se računa i vrijednost h. Napraviti usporedni prikaz za nekoliko vrijednosti h1, h2, h3 i h4
(za sve vrijednosti argumenta iz nekog zadanog skupa). Zadaje se granice intervala na kojem se računa, broj točaka u kojima se računa i vrijednost h. Napraviti usporedni prikaz za nekoliko vrijednosti h1, h2, h3 i h4
Provjerite koliko se ovako izračunata približna vrijednost derivacije razlikuje od stvarne vrijednosti derivacije. Ispitajte za funkcije sin(x) i x5
Zadatak
Odredite približnu vrijednost derivacije funkcije 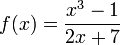 za razne vrijednosti
za razne vrijednosti  i usporedite sa stvarnom vrijednošću derivacije ove funkcije koju ste odredili pomoću sustava Wolfram Alpha
i usporedite sa stvarnom vrijednošću derivacije ove funkcije koju ste odredili pomoću sustava Wolfram Alpha
Integral
Definiramo funkciju 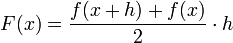 . Geometrijski, ovaj izraz predstavlja površinu trapeza s duljinama baza f(x) i f(x + h). Ova površina za "mali" h dobro aproksimira površinu ispod grafa funkcije f, na segmentu [x,x + h]. Zbrajanjem ovih površina dolazimo do formule
. Geometrijski, ovaj izraz predstavlja površinu trapeza s duljinama baza f(x) i f(x + h). Ova površina za "mali" h dobro aproksimira površinu ispod grafa funkcije f, na segmentu [x,x + h]. Zbrajanjem ovih površina dolazimo do formule 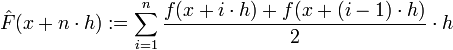 , odnosno
, odnosno 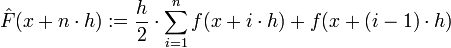
Napraviti u Excelu radni list koji računa približnu vrijednost integrala po ovoj formuli.
Izračunajte na ovaj način određene integrale nekoliko funkcija:
Za sve ove funkcije odredite vrijednost neodređenog i određenog integrala koristeći sustav Wolfram Alpha. Usporedite vrijednosti dobivene numeričkom metodom i stvarne vrijednosti
Simpsonova formula za računanje integrala
Neka je interval [a,b] podijeljen na n podintervala, pri čemu je n paran broj. Tada je složeno Simpsonovo pravilo dano sa
pri čemu je  za
za  , uz h = (b − a) / n; Posebno, x0 = a and xn = b. Gornja formula se može pisati i kao
, uz h = (b − a) / n; Posebno, x0 = a and xn = b. Gornja formula se može pisati i kao
![\begin{align}
\int_a^b f(x) \, dx & \approx
\tfrac{h}{3}\bigg[f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+\cdots+4f(x_{n-1})+f(x_n)\bigg] = \\
& = \tfrac{h}{3}\sum_{i=1}^{n/2}\bigg[f(x_{2i-2})+4f(x_{2i-1})+f(x_{2i})\bigg].\\
\end{align}](/kiwi/images/math/8/0/8/808a7a11127e92177518ed6b6bb94eb6.png)
Funkcije zadane pomoću integrala
Neke se funkcije zadaju pomoću integrale drugih funkcija. Odnosno, ako je na segmentu ![\big[a,b\big]](/kiwi/images/math/c/d/9/cd9f338e249b2e6c8ebfc3e56928a82a.png) zadana integrabilna funkcija f(x), onda možemo definirati funkciju
zadana integrabilna funkcija f(x), onda možemo definirati funkciju
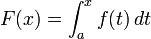
Izračunajte na ovaj način (približno pomoću Excela i toćno uvrštavanjem vrijednosti integrala funkcije f) vrijednosti funkcije 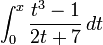 u 101 točki iz intervala
u 101 točki iz intervala ![\big[a,b\big]](/kiwi/images/math/c/d/9/cd9f338e249b2e6c8ebfc3e56928a82a.png) .
.
Nacrtajte graf obje funkcije.
Excel datoteka uz predavanja
Datoteka:Predavanja4 201503261145.zip
Euklidov algoritam
Za domaću zadaću napraviti radni list na kojem se računa najveća zajednička mjera dvaju brojeva Euklidovim algoritmom
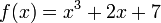
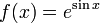
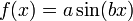
![\int_a^b f(x) \, dx\approx\tfrac{h}{3}\bigg[f(x_0)+2\sum_{j=1}^{n/2-1}f(x_{2j})+
4\sum_{j=1}^{n/2}f(x_{2j-1})+f(x_n)
\bigg],](/kiwi/images/math/f/f/2/ff27b9795842325ce6e9d94576569bb0.png)

