RP2 - Predavanje 4

Izvor: KiWi

(Usporedba među inačicama)
Skoči na: orijentacija, traži
(→Simpsonova formula za računanje integrala)
Redak 35: Redak 35:
\bigg],</math>
\bigg],</math>
-
pri čemu je <math>x_i=a+ih</math> za <math>i=0, 1, ..., n-1, n</math>, uz <math>h=(b-a)/n</math>; Posebno, <math>x_0=a</math> and <math>x_n=b</math>. Gornja formula se može pisati i kao
+
pri čemu je <math>\ x_i=a+ih</math> za <math>\ i=0, 1, ..., n-1, n</math>, uz <math>h=(b-a)/n</math>; Posebno, <math>x_0=a</math> and <math>x_n=b</math>. Gornja formula se može pisati i kao
:<math>\int_a^b f(x) \, dx\approx
:<math>\int_a^b f(x) \, dx\approx
\tfrac{h}{3}\bigg[f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+\cdots+4f(x_{n-1})+f(x_n)\bigg]
\tfrac{h}{3}\bigg[f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+\cdots+4f(x_{n-1})+f(x_n)\bigg]
=\tfrac{h}{3}\sum_{i=1}^{n/2}\bigg[f(x_{2i-2})+4f(x_{2i-1})+f(x_{2i})\bigg].</math>
=\tfrac{h}{3}\sum_{i=1}^{n/2}\bigg[f(x_{2i-2})+4f(x_{2i-1})+f(x_{2i})\bigg].</math>
-
 
== Euklidov algoritam ==
== Euklidov algoritam ==
Za domaću zadaću napraviti radni list na kojem se računa najveća zajednička mjera dvaju brojeva [http://en.wikipedia.org/wiki/Euclidean_algorithm Euklidovim algoritmom]
Za domaću zadaću napraviti radni list na kojem se računa najveća zajednička mjera dvaju brojeva [http://en.wikipedia.org/wiki/Euclidean_algorithm Euklidovim algoritmom]

Inačica od 11:05, 26. ožujka 2014.

Sadržaj

Derivacija

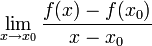
Derivacija funkcije u točki x0 definira se kao \lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}

Približna vrijednost derivacije može se odrediti tako da se za dani h > 0 računa kvocijent diferencija 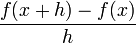\frac{f(x+h)-f(x)}{h}.

Napravite u Excelu tablicu koja će za dani h > 0 računati 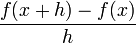\frac{f(x+h)-f(x)}{h} (za sve vrijednosti argumenta iz nekog zadanog skupa). Zadaje se granice intervala na kojem se računa, broj točaka u kojima se računa i vrijednost h. Napraviti usporedni prikaz za nekoliko vrijednosti h1, h2, h3 i h4

Provjerite koliko se ovako izračunata približna vrijednost derivacije razlikuje od stvarne vrijednosti derivacije. Ispitajte za funkcije sin(x) i x5

Integral

Definiramo funkciju 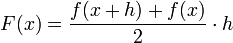F(x)=\frac{f(x+h)+f(x)}{2}\cdot h. Geometrijski, ovaj izraz predstavlja površinu trapeza s duljinama baza f(x) i f(x + h). Ova površina za "mali" h dobro aproksimira površinu ispod grafa funkcije f, na segmentu [x,x + h]. Zbrajanjem ovih površina dolazimo do formule 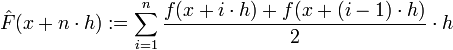\hat{F}(x+n\cdot h):=\sum_{i=1}^n \frac{f(x+i\cdot h)+f(x+(i-1)\cdot h)}{2}\cdot h, odnosno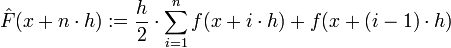 \hat{F}(x+n\cdot h):=\frac{h}{2} \cdot\sum_{i=1}^n f(x+i\cdot h)+f(x+(i-1)\cdot h)

Napraviti u Excelu radni list koji računa približnu vrijednost integrala po ovoj formuli.

Izračunajte na ovaj način određene integrale nekoliko funkcija:

  • \ f(x)=x^3+2x+7
  • f(x)=\frac{x^3-1}{2x+7}
  • \ f(x)=e^{\sin x}
  • \ f(x)=a \sin (b x)

Simpsonova formula za računanje integrala

Neka je interval [a,b] podijeljen na n podintervala, pri čemu je n paran broj. Tada je složeno Simpsonovo pravilo dano sa

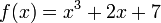
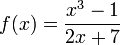
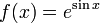
\int_a^b f(x) \, dx\approx\tfrac{h}{3}\bigg[f(x_0)+2\sum_{j=1}^{n/2-1}f(x_{2j})+ 4\sum_{j=1}^{n/2}f(x_{2j-1})+f(x_n) \bigg],

pri čemu je \ x_i=a+ih za \ i=0, 1, ..., n-1, n, uz h = (b − a) / n; Posebno, x0 = a and xn = b. Gornja formula se može pisati i kao

\int_a^b f(x) \, dx\approx \tfrac{h}{3}\bigg[f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+\cdots+4f(x_{n-1})+f(x_n)\bigg] =\tfrac{h}{3}\sum_{i=1}^{n/2}\bigg[f(x_{2i-2})+4f(x_{2i-1})+f(x_{2i})\bigg].

Euklidov algoritam

Za domaću zadaću napraviti radni list na kojem se računa najveća zajednička mjera dvaju brojeva Euklidovim algoritmom

Dobavljeno iz "http://degiorgi.math.hr/kiwi/index.php/RP2_-_Predavanje_4"
Osobni alati