RP2 - Predavanje 4

Izvor: KiWi

Inačica od 15:52, 6. ožujka 2012. koju je unio/unijela Goranigaly (Razgovor | doprinosi)
Skoči na: orijentacija, traži

Derivacija

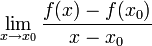
Derivacija funkcije u točki x0 definira se kao \lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}

Približna vrijednost derivacije može se odrediti tako da se za dani h > 0 računa kvocijent diferencija 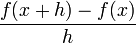\frac{f(x+h)-f(x)}{h}.

Napravite u Excelu tablicu koja će za dani h>0 računati 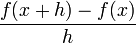\frac{f(x+h)-f(x)}{h} (za sve vrijednosti argumenta iz nekog zadanog skupa)

Provjerite koliko se ovako izračunata približna vrijednost derivacije razlikuje od stvarne vrijednosti derivacije. Ispitajte za funkcije sin(x) i x5

Integral

Definiramo funkciju 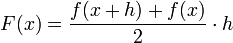F(x)=\frac{f(x+h)+f(x)}{2}\cdot h. Geometrijski, ovaj izraz predstavlja površinu trapeza s duljinama baza f(x) i f(x + h). Ova površina za "mali" h dobro aproksimira površinu ispod grafa funkcije f, na segmentu [x,x + h]. Zbrajanjem ovih površina dolazimo do formule 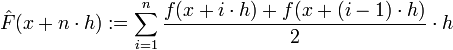\hat{F}(x+n\cdot h):=\sum_{i=1}^n \frac{f(x+i\cdot h)+f(x+(i-1)\cdot h)}{2}\cdot h, odnosno Obrada nije uspjela. (sintaksna pogreška): \hat{F}(x+n\cdot h):=\frac{h}{2} \cdot\sum_{i=1}^n f(x+i\cdot h)+f(x+(i-1))}

Dobavljeno iz "http://degiorgi.math.hr/kiwi/index.php/RP2_-_Predavanje_4"
Osobni alati