| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
|
| [Vrh] |
|
iuppiter
Forumaš(ica)

Pridružen/a: 03. 01. 2006. (12:15:51)
Postovi: (6A)16
Spol: 
Lokacija: Nigdjezemska
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 19:16 uto, 10. 7. 2007 Naslov: Postano: 19:16 uto, 10. 7. 2007 Naslov: |
    |
|
|
[quote="iuppiter"]Malo sam se spetljala i malo mi u ovome nešto nije jasno:
Naime, ako imam f homo, f(xy^-1)=f(e) f-ove mogu maknuti samo ako je Kerf={e}, a inace ne? Raspisala sam si onaj zadatak s vježbi di treba dokazati da je f mono akko Kerf={e} pa zato pitam.[/quote]
f mozes maknut akko je f injekcija.
[quote="iuppiter"]I da li ako je H1<H nužno praslika(H)<G? Mislim da ne, al neznam objasnit.[/quote]
Ne razumijem pitanje :?:
| iuppiter (napisa): | Malo sam se spetljala i malo mi u ovome nešto nije jasno:
Naime, ako imam f homo, f(xy^-1)=f(e) f-ove mogu maknuti samo ako je Kerf={e}, a inace ne? Raspisala sam si onaj zadatak s vježbi di treba dokazati da je f mono akko Kerf={e} pa zato pitam. |
f mozes maknut akko je f injekcija.
| iuppiter (napisa): | | I da li ako je H1<H nužno praslika(H)<G? Mislim da ne, al neznam objasnit. |
Ne razumijem pitanje 
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
Gost
|
 Postano: 20:26 uto, 10. 7. 2007 Naslov: Postano: 20:26 uto, 10. 7. 2007 Naslov: |
    |
|
|
[quote="iuppiter"]
I da li ako je H1<H nužno praslika(H)<G? Mislim da ne, al neznam objasnit.[/quote]
Sada ćemo mi to tebi objasnit.
Neka je f : G -> H homo, H1<H. Tada je
G1 : =f^-1(H1) = {x iz G| f(x) iz H1} < G.
Uzmemo a, b iz G1. Tada su po pretpostavci f(a), f(b) iz H1, pa kako je
H1 < H, slijedi da je f(a)f(b)^-1 iz H1. U drugu ruku imaš f(b^-1) = f(b)^-1, pa je f(ab^-1) = f(a)f(b)^-1, tj. ab^-1 iz G1.
Sretno.
| iuppiter (napisa): |
I da li ako je H1<H nužno praslika(H)<G? Mislim da ne, al neznam objasnit. |
Sada ćemo mi to tebi objasnit.
Neka je f : G → H homo, H1<H. Tada je
G1 : =f^-1(H1) = {x iz G| f(x) iz H1} < G.
Uzmemo a, b iz G1. Tada su po pretpostavci f(a), f(b) iz H1, pa kako je
H1 < H, slijedi da je f(a)f(b)^-1 iz H1. U drugu ruku imaš f(b^-1) = f(b)^-1, pa je f(ab^-1) = f(a)f(b)^-1, tj. ab^-1 iz G1.
Sretno.
|
|
| [Vrh] |
|
iuppiter
Forumaš(ica)

Pridružen/a: 03. 01. 2006. (12:15:51)
Postovi: (6A)16
Spol: 
Lokacija: Nigdjezemska
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
iuppiter
Forumaš(ica)

Pridružen/a: 03. 01. 2006. (12:15:51)
Postovi: (6A)16
Spol: 
Lokacija: Nigdjezemska
|
 Postano: 23:00 uto, 10. 7. 2007 Naslov: Postano: 23:00 uto, 10. 7. 2007 Naslov: |
    |
|
|
[quote="Anonymous"]
Općenito: f :A -> B je INJEKCIJA :<=> (za sve a, b iz A) a = b <=> f(a) = f(b). Monomorfizam je homo koji je injekcija.
nhf, ali stvari o kojima se ti raspituješ su jaaaaako laaaaagane.[/quote]
non taken...hehe...znam...sram me :oops: , ali kad se na banaliji o kojoj nikad ni ne razmišljam padne usmeni (a dogodilo mi se to u petak) , bolje pitati nego pasti... (iskreno u gornjoj tvrdnji sam razmišljala samo ==>, a ne <==>)
| Anonymous (napisa): |
Općenito: f :A → B je INJEKCIJA :⇔ (za sve a, b iz A) a = b ⇔ f(a) = f(b). Monomorfizam je homo koji je injekcija.
nhf, ali stvari o kojima se ti raspituješ su jaaaaako laaaaagane. |
non taken...hehe...znam...sram me  , ali kad se na banaliji o kojoj nikad ni ne razmišljam padne usmeni (a dogodilo mi se to u petak) , bolje pitati nego pasti... (iskreno u gornjoj tvrdnji sam razmišljala samo ⇒, a ne ⇔) , ali kad se na banaliji o kojoj nikad ni ne razmišljam padne usmeni (a dogodilo mi se to u petak) , bolje pitati nego pasti... (iskreno u gornjoj tvrdnji sam razmišljala samo ⇒, a ne ⇔)
_________________
Stultorum plena sunt omnia.
/Ciceron/
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 9:54 sri, 11. 7. 2007 Naslov: Postano: 9:54 sri, 11. 7. 2007 Naslov: |
    |
|
|
[quote="iuppiter"][quote="Martinab"]
f mozes maknut akko je f injekcija.
[/quote]
u biljeznici iz vjezbi imam u dijelu zadatka gdje se dokazuje smjer ako Kerf={e} onda f mono samo maknute f-ove ( tj iz f(xy^-1)=f(e) slijedi xy^-1=e )...il sam krivo prepisala/shvatila ili sam nešto propustila...
btw tnx Martina & gost :D :D[/quote]
Ok, sad kuzim kaj ti nije jasno. Nije ti jasno zakaj smijes skinut f-ove iz f(xy^-1)=f(e) ako ti je pretpostavka samo da je Kerf={e}, a jos ne znas (dokazujes) da je injekcija. Sori, nisam to skuzila prije.
Spika je ova: Ker f ={g iz G| f(g)=e}. Pa ako je Ker f ={e}, onda cim imas f(z)=e mozes zakljucit z=e. U tvom primjeru, imas f(xy^-1)=f(e)=e, dakle xy^{-1} je iz Ker f, pa je xy^{-1}=e. Tako STVARNO koristis samo pretpostavku Kerf={e} a ne i injektivnost koju pokusavas dokazat.
| iuppiter (napisa): | | Martinab (napisa): |
f mozes maknut akko je f injekcija.
|
u biljeznici iz vjezbi imam u dijelu zadatka gdje se dokazuje smjer ako Kerf={e} onda f mono samo maknute f-ove ( tj iz f(xy^-1)=f(e) slijedi xy^-1=e )...il sam krivo prepisala/shvatila ili sam nešto propustila...
btw tnx Martina & gost   |
Ok, sad kuzim kaj ti nije jasno. Nije ti jasno zakaj smijes skinut f-ove iz f(xy^-1)=f(e) ako ti je pretpostavka samo da je Kerf={e}, a jos ne znas (dokazujes) da je injekcija. Sori, nisam to skuzila prije.
Spika je ova: Ker f ={g iz G| f(g)=e}. Pa ako je Ker f ={e}, onda cim imas f(z)=e mozes zakljucit z=e. U tvom primjeru, imas f(xy^-1)=f(e)=e, dakle xy^{-1} je iz Ker f, pa je xy^{-1}=e. Tako STVARNO koristis samo pretpostavku Kerf={e} a ne i injektivnost koju pokusavas dokazat.
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
sanja86
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (11:19:30)
Postovi: (F)16
Lokacija: nigdjezemska
|
 Postano: 18:29 uto, 15. 7. 2008 Naslov: Postano: 18:29 uto, 15. 7. 2008 Naslov: |
    |
|
|
molila bih, ako ima neka dobra duša da ni rješi 4 adatak sa ovogodišnjeg 2 kolokvija :(
ispitaje da li je ideal (7+3i, 3+i) u prstenu Z[i] glavni?
polkažite ga kao glavni ideal. je li prost i maksimalan ispitajte.
u principu znam kako rješit, problem nastaje što ne mogu nać NZM od ova dva (prie uspjela, sad nemogu pnovit :oops: )
pa, ako se nekom bar to da raspisat :moli:
molila bih, ako ima neka dobra duša da ni rješi 4 adatak sa ovogodišnjeg 2 kolokvija 
ispitaje da li je ideal (7+3i, 3+i) u prstenu Z[i] glavni?
polkažite ga kao glavni ideal. je li prost i maksimalan ispitajte.
u principu znam kako rješit, problem nastaje što ne mogu nać NZM od ova dva (prie uspjela, sad nemogu pnovit  ) )
pa, ako se nekom bar to da raspisat :moli:
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 21:47 uto, 15. 7. 2008 Naslov: Postano: 21:47 uto, 15. 7. 2008 Naslov: |
    |
|
|
[quote="sanja86"]molila bih, ako ima neka dobra duša da ni rješi 4 adatak sa ovogodišnjeg 2 kolokvija :(
ispitaje da li je ideal (7+3i, 3+i) u prstenu Z[i] glavni?
polkažite ga kao glavni ideal. je li prost i maksimalan ispitajte.
u principu znam kako rješit, problem nastaje što ne mogu nać NZM od ova dva (prie uspjela, sad nemogu pnovit :oops: )
pa, ako se nekom bar to da raspisat :moli:[/quote]
ono što radiš je zapravo euklidov algoritam.
želimo [latex]q, r[/latex] takve da je [latex]7+3i = (3+i)q + r[/latex].
radimo u prstenu [latex]\mathbb{Z}[i][/latex], pa nam je dovoljno naći neki [latex]q[/latex] takav da [latex](3+i)q[/latex] bude "dovoljno blizu" [latex]7+3i[/latex]. "dovoljno blizu" znači da je [latex]|r|<|3+i|[/latex].
zamisli si cjelobrojnu mrežu u ravnini. [latex]q[/latex] će biti točka s cjelobrojnim koordinatama najbliža kvocijentu [latex]\frac{7+3i}{3+i}[/latex]. nakon pronalaska [latex]q[/latex], [latex]r[/latex] je lako izračunati. taj korak poslije ponavljaš dok ostatak ne bude 0.
dakle, [latex]\frac{7+3i}{3+i} = \frac{(7+3i)(3-i)}{(3+i)(3-i)} = \frac{12+i}{5}[/latex]. ovako na prvi pogled, čini se da bi dobar [latex]q[/latex] mogao biti 2.
tada imamo: [latex]7+3i = 2(3+i) + r[/latex], iz čega imamo: [latex]r=1+i[/latex]. to nam je u redu jer [latex]|1+i|<|3+i|[/latex].
u drugom koraku tražimo [latex]q_1, r_1[/latex] takve da [latex]3+i = (1+i)q_1 + r_1[/latex]. no sada [latex]\frac{3+i}{1+i}=2-i[/latex], što znači da je [latex]r_1 = 0[/latex], pa uzimamo [latex]NZM(7+3i,3+i)=1+i[/latex].
ovaj broj nije jedinstven. vidi se da je, primjerice, i [latex]<1-i>[/latex] isti ideal.
| sanja86 (napisa): | molila bih, ako ima neka dobra duša da ni rješi 4 adatak sa ovogodišnjeg 2 kolokvija 
ispitaje da li je ideal (7+3i, 3+i) u prstenu Z[i] glavni?
polkažite ga kao glavni ideal. je li prost i maksimalan ispitajte.
u principu znam kako rješit, problem nastaje što ne mogu nać NZM od ova dva (prie uspjela, sad nemogu pnovit  ) )
pa, ako se nekom bar to da raspisat :moli: |
ono što radiš je zapravo euklidov algoritam.
želimo 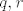 takve da je takve da je 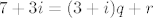 . .
radimo u prstenu 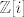 , pa nam je dovoljno naći neki , pa nam je dovoljno naći neki  takav da takav da 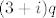 bude "dovoljno blizu" bude "dovoljno blizu"  . "dovoljno blizu" znači da je . "dovoljno blizu" znači da je 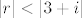 . .
zamisli si cjelobrojnu mrežu u ravnini.  će biti točka s cjelobrojnim koordinatama najbliža kvocijentu će biti točka s cjelobrojnim koordinatama najbliža kvocijentu 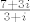 . nakon pronalaska . nakon pronalaska  , ,  je lako izračunati. taj korak poslije ponavljaš dok ostatak ne bude 0. je lako izračunati. taj korak poslije ponavljaš dok ostatak ne bude 0.
dakle, 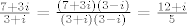 . ovako na prvi pogled, čini se da bi dobar . ovako na prvi pogled, čini se da bi dobar  mogao biti 2. mogao biti 2.
tada imamo: 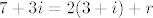 , iz čega imamo: , iz čega imamo: 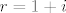 . to nam je u redu jer . to nam je u redu jer 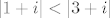 . .
u drugom koraku tražimo 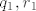 takve da takve da 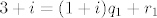 . no sada . no sada 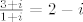 , što znači da je , što znači da je 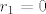 , pa uzimamo , pa uzimamo 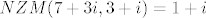 . .
ovaj broj nije jedinstven. vidi se da je, primjerice, i 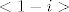 isti ideal. isti ideal.
_________________
ima let u finish
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Lara
Forumaš(ica)


Pridružen/a: 17. 01. 2007. (16:23:54)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
vini
Forumaš(ica)


Pridružen/a: 01. 09. 2006. (18:10:50)
Postovi: (9E)16
Spol: 
|
 Postano: 16:34 ned, 7. 9. 2008 Naslov: Postano: 16:34 ned, 7. 9. 2008 Naslov: |
    |
|
|
[quote="ma"][quote="sanja86"]molila bih, ako ima neka dobra duša da ni rješi 4 adatak sa ovogodišnjeg 2 kolokvija :(
ispitaje da li je ideal (7+3i, 3+i) u prstenu Z[i] glavni?
polkažite ga kao glavni ideal. je li prost i maksimalan ispitajte.
u principu znam kako rješit, problem nastaje što ne mogu nać NZM od ova dva (prie uspjela, sad nemogu pnovit :oops: )
pa, ako se nekom bar to da raspisat :moli:[/quote]
ono što radiš je zapravo euklidov algoritam.
želimo [latex]q, r[/latex] takve da je [latex]7+3i = (3+i)q + r[/latex].
radimo u prstenu [latex]\mathbb{Z}[i][/latex], pa nam je dovoljno naći neki [latex]q[/latex] takav da [latex](3+i)q[/latex] bude "dovoljno blizu" [latex]7+3i[/latex]. "dovoljno blizu" znači da je [latex]|r|<|3+i|[/latex].
zamisli si cjelobrojnu mrežu u ravnini. [latex]q[/latex] će biti točka s cjelobrojnim koordinatama najbliža kvocijentu [latex]\frac{7+3i}{3+i}[/latex]. nakon pronalaska [latex]q[/latex], [latex]r[/latex] je lako izračunati. taj korak poslije ponavljaš dok ostatak ne bude 0.
dakle, [latex]\frac{7+3i}{3+i} = \frac{(7+3i)(3-i)}{(3+i)(3-i)} = \frac{12+i}{5}[/latex]. ovako na prvi pogled, čini se da bi dobar [latex]q[/latex] mogao biti 2.
tada imamo: [latex]7+3i = 2(3+i) + r[/latex], iz čega imamo: [latex]r=1+i[/latex]. to nam je u redu jer [latex]|1+i|<|3+i|[/latex].
u drugom koraku tražimo [latex]q_1, r_1[/latex] takve da [latex]3+i = (1+i)q_1 + r_1[/latex]. no sada [latex]\frac{3+i}{1+i}=2-i[/latex], što znači da je [latex]r_1 = 0[/latex], pa uzimamo [latex]NZM(7+3i,3+i)=1+i[/latex].
ovaj broj nije jedinstven. vidi se da je, primjerice, i [latex]<1-i>[/latex] isti ideal.[/quote]
Moze li netko molim vas raspisat drugi dio zadatka?! Da li je ideal (7+3i, 3+i) prost i maksimalan?
Treba pokazat da je ideal (7+3i, 3+i) ireducibilan...a ja ne znam kako :(
Unaprijed zahvalna na pomoci
| ma (napisa): | | sanja86 (napisa): | molila bih, ako ima neka dobra duša da ni rješi 4 adatak sa ovogodišnjeg 2 kolokvija 
ispitaje da li je ideal (7+3i, 3+i) u prstenu Z[i] glavni?
polkažite ga kao glavni ideal. je li prost i maksimalan ispitajte.
u principu znam kako rješit, problem nastaje što ne mogu nać NZM od ova dva (prie uspjela, sad nemogu pnovit  ) )
pa, ako se nekom bar to da raspisat :moli: |
ono što radiš je zapravo euklidov algoritam.
želimo 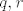 takve da je takve da je 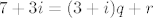 . .
radimo u prstenu 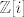 , pa nam je dovoljno naći neki , pa nam je dovoljno naći neki  takav da takav da 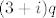 bude "dovoljno blizu" bude "dovoljno blizu"  . "dovoljno blizu" znači da je . "dovoljno blizu" znači da je 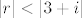 . .
zamisli si cjelobrojnu mrežu u ravnini.  će biti točka s cjelobrojnim koordinatama najbliža kvocijentu će biti točka s cjelobrojnim koordinatama najbliža kvocijentu 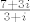 . nakon pronalaska . nakon pronalaska  , ,  je lako izračunati. taj korak poslije ponavljaš dok ostatak ne bude 0. je lako izračunati. taj korak poslije ponavljaš dok ostatak ne bude 0.
dakle, 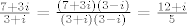 . ovako na prvi pogled, čini se da bi dobar . ovako na prvi pogled, čini se da bi dobar  mogao biti 2. mogao biti 2.
tada imamo: 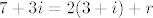 , iz čega imamo: , iz čega imamo: 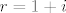 . to nam je u redu jer . to nam je u redu jer 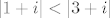 . .
u drugom koraku tražimo 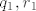 takve da takve da 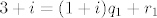 . no sada . no sada 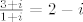 , što znači da je , što znači da je 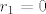 , pa uzimamo , pa uzimamo 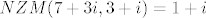 . .
ovaj broj nije jedinstven. vidi se da je, primjerice, i 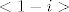 isti ideal. isti ideal. |
Moze li netko molim vas raspisat drugi dio zadatka?! Da li je ideal (7+3i, 3+i) prost i maksimalan?
Treba pokazat da je ideal (7+3i, 3+i) ireducibilan...a ja ne znam kako 
Unaprijed zahvalna na pomoci
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:14 ned, 7. 9. 2008 Naslov: Postano: 17:14 ned, 7. 9. 2008 Naslov: |
    |
|
|
[quote="vini"]
Moze li netko molim vas raspisat drugi dio zadatka?! Da li je ideal (7+3i, 3+i) prost i maksimalan?
Treba pokazat da je ideal (7+3i, 3+i) ireducibilan...a ja ne znam kako :(
Unaprijed zahvalna na pomoci[/quote]
To gledaš preko one norme... tj imaš da je N(x+yi)=x^2+y^2 (valjda) i imaš da je element ireduc ako se može prikazati kao a*b, gdje je a ireduc ili b ireduc... (tj ako je N(a)=+-1 ili N(b)=+-1.
E sad, ovaj ideal se može prikazat kao glavni, pa onda za taj elemnet gledaš dal je ireduc...
Eto, to je ideja. :D
| vini (napisa): |
Moze li netko molim vas raspisat drugi dio zadatka?! Da li je ideal (7+3i, 3+i) prost i maksimalan?
Treba pokazat da je ideal (7+3i, 3+i) ireducibilan...a ja ne znam kako 
Unaprijed zahvalna na pomoci |
To gledaš preko one norme... tj imaš da je N(x+yi)=x^2+y^2 (valjda) i imaš da je element ireduc ako se može prikazati kao a*b, gdje je a ireduc ili b ireduc... (tj ako je N(a)=+-1 ili N(b)=+-1.
E sad, ovaj ideal se može prikazat kao glavni, pa onda za taj elemnet gledaš dal je ireduc...
Eto, to je ideja. 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
blabla
Forumaš(ica)

Pridružen/a: 02. 09. 2007. (15:39:56)
Postovi: (13)16
Spol: 
|
 Postano: 12:15 uto, 9. 9. 2008 Naslov: Postano: 12:15 uto, 9. 9. 2008 Naslov: |
    |
|
|
molim pomoc u vezi ovog zadatka:
Dokazite da postoji jedinstvena, do na izomorfizam, beskonacna ciklicka grupa.
Ja sam krenula ovako_Znamo da su sve beskonacne ciklicke grupe izomorfne Z. Neka je G beskonacna cikl grupa t.d. G=(a)={..., aˆ(-1), e, a, ...}, a el iz G. Def. f:G->Z f(aˆk)=k. Ocito, f je izomorfizam.
jel to jedini izomorfizam pa je tvrdnja dokazana ili...?
hvala :)
molim pomoc u vezi ovog zadatka:
Dokazite da postoji jedinstvena, do na izomorfizam, beskonacna ciklicka grupa.
Ja sam krenula ovako_Znamo da su sve beskonacne ciklicke grupe izomorfne Z. Neka je G beskonacna cikl grupa t.d. G=(a)={..., aˆ(-1), e, a, ...}, a el iz G. Def. f:G->Z f(aˆk)=k. Ocito, f je izomorfizam.
jel to jedini izomorfizam pa je tvrdnja dokazana ili...?
hvala 
_________________  |
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
blabla
Forumaš(ica)

Pridružen/a: 02. 09. 2007. (15:39:56)
Postovi: (13)16
Spol: 
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 15:25 uto, 9. 9. 2008 Naslov: Postano: 15:25 uto, 9. 9. 2008 Naslov: |
    |
|
|
[quote="blabla"]
Dokazite da postoji jedinstvena, do na izomorfizam, beskonacna ciklicka grupa.
Ja sam krenula ovako_Znamo da su sve beskonacne ciklicke grupe izomorfne Z. ... [/quote]
Hm, ako ZNAS da su sve beskonacne ciklicke grupe izormorfne sa Z, onda nemas kaj dokazivat, ne? Tocno to je tvrdnja koju moras dokazat...
| blabla (napisa): |
Dokazite da postoji jedinstvena, do na izomorfizam, beskonacna ciklicka grupa.
Ja sam krenula ovako_Znamo da su sve beskonacne ciklicke grupe izomorfne Z. ... |
Hm, ako ZNAS da su sve beskonacne ciklicke grupe izormorfne sa Z, onda nemas kaj dokazivat, ne? Tocno to je tvrdnja koju moras dokazat...
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
UpitniKlik
Gost
|
|
| [Vrh] |
|
|
















