|
Simple, to je realna ravnina kojoj si "izvadio" sve tocke kojima su - kljucni dio - [b]obje[/b] koordinate racionalne. :) Recimo da imas tocke
[latex]A = (x_A, y_A)[/latex] i [latex]B = (x_B, y_B)[/latex] takve da je [latex]A, B \in \mathbb{R}^2 \setminus \mathbb{Q}^2[/latex].
To znaci da je za svaku tocku barem jedna koordinata iracionalna.
Uvedimo tocku C kojoj su obje koordinate iracionalne, na primjer [latex]C = (\pi, \pi)[/latex].
Recimo da je [latex]x_A \in \mathbb{R} \setminus \mathbb{Q}[/latex]. Sada fino krenes iz tocke A vertikalno prema C. Kako koordinatu x ne mijenjas, ona ce stalno biti iracionalna, pa ce i sve tocke biti u skupu koji te zanima:
[latex](x_A, ty_A+(1-t)y_C) \in \mathbb{R}^2 \setminus \mathbb{Q}^2, \quad t \in [0,1][/latex].
Nakon toga krenes horizontalno prema C, sto smijes jer je [latex]y_C \in \mathbb{R} \setminus \mathbb{Q}[/latex]:
[latex](tx_A+(1-t)x_C, y_C) \in \mathbb{R}^2 \setminus \mathbb{Q}^2, \quad t \in [0,1][/latex].
Analogno bi isao iz A u C kad bi bilo [latex]x_A \in \mathbb{Q}[/latex]; jedina je razlika da bi prvo isao horizontalno.
Na isti nacin ides od C do B. 8)
Zasto ne direktno od A do B? Recimo, za tocke
[latex]A = (\pi, 0), \quad B = (2\pi, 0)[/latex]
ne mozes ici ravno, nego treba zaobici tocke oblika
[latex](x, 0), \quad x \in [\pi,2\pi] \cap \mathbb{Q}[/latex].
HTH. :D
Simple, to je realna ravnina kojoj si "izvadio" sve tocke kojima su - kljucni dio - obje koordinate racionalne.  Recimo da imas tocke Recimo da imas tocke
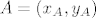 i i 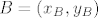 takve da je takve da je 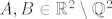 . .
To znaci da je za svaku tocku barem jedna koordinata iracionalna.
Uvedimo tocku C kojoj su obje koordinate iracionalne, na primjer 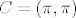 . .
Recimo da je 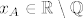 . Sada fino krenes iz tocke A vertikalno prema C. Kako koordinatu x ne mijenjas, ona ce stalno biti iracionalna, pa ce i sve tocke biti u skupu koji te zanima: . Sada fino krenes iz tocke A vertikalno prema C. Kako koordinatu x ne mijenjas, ona ce stalno biti iracionalna, pa ce i sve tocke biti u skupu koji te zanima:
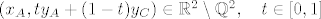 . .
Nakon toga krenes horizontalno prema C, sto smijes jer je 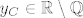 : :
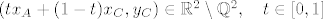 . .
Analogno bi isao iz A u C kad bi bilo 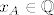 ; jedina je razlika da bi prvo isao horizontalno. ; jedina je razlika da bi prvo isao horizontalno.
Na isti nacin ides od C do B. 
Zasto ne direktno od A do B? Recimo, za tocke

ne mozes ici ravno, nego treba zaobici tocke oblika
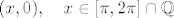 . .
HTH. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |





