| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Neznalica
Forumaš(ica)

Pridružen/a: 07. 01. 2009. (22:26:13)
Postovi: (6)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:36 sri, 7. 1. 2009 Naslov: Postano: 22:36 sri, 7. 1. 2009 Naslov: |
    |
|
|
Ovako postavljen zadatak ti neće riješiti nitko... nisi reko/rekla kaj se traži, ni što predstavlja koje slovo. Budi precizniji/preciznija
Ovako postavljen zadatak ti neće riješiti nitko... nisi reko/rekla kaj se traži, ni što predstavlja koje slovo. Budi precizniji/preciznija
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Neznalica
Forumaš(ica)

Pridružen/a: 07. 01. 2009. (22:26:13)
Postovi: (6)16
|
|
| [Vrh] |
|
zeix
Forumaš(ica)

Pridružen/a: 18. 02. 2006. (12:39:11)
Postovi: (75)16
|
 Postano: 0:20 čet, 8. 1. 2009 Naslov: Postano: 0:20 čet, 8. 1. 2009 Naslov: |
    |
|
|
Da, ovo je Einsteinova jednadzba iz opce teorije relativnosti. Ali da bi je rijesija mora ti biti zadan i ovaj T u jednadzbi. Taj T je tenzor energije-impulsa kolko se ja sicam i on se mora zadati. Npr, za vakum je T=0 pa onda postoji egzaktno rjesenje jednadzbe. Ali ako taj T opisuje nekoliko planeta i asteroida, ona nema sanse da to je rjesis. Drugim rjecima, preaj okladu :D
Da, ovo je Einsteinova jednadzba iz opce teorije relativnosti. Ali da bi je rijesija mora ti biti zadan i ovaj T u jednadzbi. Taj T je tenzor energije-impulsa kolko se ja sicam i on se mora zadati. Npr, za vakum je T=0 pa onda postoji egzaktno rjesenje jednadzbe. Ali ako taj T opisuje nekoliko planeta i asteroida, ona nema sanse da to je rjesis. Drugim rjecima, preaj okladu 
_________________
"From this proposition it will follow, when arithmetical addition has been defined, that 1+1=2."
Page 360, Principia Mathematica
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 15:05 čet, 8. 1. 2009 Naslov: Re: Rµv-1/2gµvR-λgµv=-8πGTµv Postano: 15:05 čet, 8. 1. 2009 Naslov: Re: Rµv-1/2gµvR-λgµv=-8πGTµv |
    |
|
|
[quote="Neznalica"]Evo jednog zadatka i hitno trebam rješenje. zadatak glasi ovako:
Rµv-1/2gµvR-λgµv=-8πGTµv molim vas rješenje[/quote]
[latex]R_{\mu\nu}[/latex] predstavlja Ricci-jev tenzor, koji opisuje volumnu distorziju prostora. [latex]g_{\mu\nu}[/latex] predstavlja metriku prostor-vremena, [latex]\Lambda[/latex] predstavlja kozmolosku konstantu, R predstavlja Riccijev skalar, G je gravitacijska konstanta, a [latex]T_{\mu\nu}[/latex] predstavlja tenzor energije-impulsa. u slucaju da je tenzor energije-impulsa jednak 0 i kozmoloska konstanta jednaka 0, onda se jednadzba svodi na vakuumsku jednadzbu [latex]R_{\mu\nu}=0[/latex], a u slucaju da je [latex]\Lambda \neq 0[/latex], onda se jednadzba svodi na [latex]R_{\mu\nu}=\Lambda g_{\mu\nu}[/latex]. ovo su trivijalna rjesenja Einsteinovih jedndazbi koje predstavljaju osnovu opce teorije relativnosti. postoje i netrivijalna rjesenja, kao primjerice Schwarzschildova metrika (koja opisuje gravitacijsko polje van neke sferne nerotirajuce mase, tipicno planeta ili crne rupe, ali se moze koristiti za bilo koju takvu nerotirajucu sfernu masu) te primjerice Kerrova metrika koja takodjer opisuje geometriju prostor-vremena oko neke sferne mase. razlika izmedju dva rjesenja jest sto ta masa u slucaju Kerrovog rjesenja rotira. njegovo rjesenje za geometriju prostor-vremena oko sferne mase M koja rotira sa angularnim momentom J se moze napisati u obliku matematicke formule:
[latex]c^2\text{d}\tau=\Big ( 1-\frac{r_s r}{\rho^2} \Big )c^2 \text{d}t^2-\frac{\rho^2}{\Lambda^2}\text{d}r^2-\rho^2\text{d}\theta^2[/latex][latex]-\Big (r^2+\alpha^2+\frac{r_s r\alpha^2}{\rho^2}\sin^2\theta \Big ) \sin^2\theta \text{d}\phi+\frac{2r_s r\alpha\sin^2\theta}{\rho}c\text{d}t\text{d}\phi[/latex]
gdje su koordinate [latex]r,\, \phi, \, \theta[/latex] standardne koordinate u sfernom koordinatnom sustavu. a [latex]r_s[/latex] Schwarzschildov radijus [latex]r_s=\frac{2GM}{c^2}[/latex]. ostale konstante su tu zbog kraceg zapisa:
[latex]\alpha=\frac{J}{Mc}[/latex],[latex]\; \rho^2=r^2+\alpha^2\cos^2\theta[/latex], [latex]\; \Lambda^2=r^2-r_s r+\alpha^2[/latex].
Kerrova metrika i Kerrovo rjesenje je bitno jer su u realnom slucaju (dakle, u nasem svemiru) crne rupe i opcenito sferne mase koje nemaju rotaciju vrlo rijetke. u tom smislu, Schwarzschildova metrika je samo jako pojednostavljen slucaj. sve crne rupe (koje su i bile jedan od fenomena koje je teorijski pretpostavila opca teorija relativnosti) za koje danas znamo imaju neku kolicinu angularnog momenta, odnosno neku rotaciju.
problem kod rjesenja Einsteinovih jednadzbi jest u tome sto su jednadzbe iznimno nelinearne. u tom smislu, naci egzaktno rjesenje je vrlo tesko, a nekad gotovo i nemoguce. zbog toga, danas se rjesenja Einsteinovih jednadzbi uglavnom izracunavaju pomocu racunalnih simulacija na super-racunalima.
HTH.
btw. ima jako puno o tome na Wikipediiji, pa tko hoce, moze tamo naci dosta odgovora. ovo je, sa stanovista fizike, jos uvijek vrlo zanimljivo podrucje, podrucje koje jos uvijek nije dalo maksimum, kako teorijskog tako i eksperimentalnog, istrazivanja.
| Neznalica (napisa): | Evo jednog zadatka i hitno trebam rješenje. zadatak glasi ovako:
Rµv-1/2gµvR-λgµv=-8πGTµv molim vas rješenje |
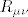 predstavlja Ricci-jev tenzor, koji opisuje volumnu distorziju prostora. predstavlja Ricci-jev tenzor, koji opisuje volumnu distorziju prostora. 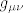 predstavlja metriku prostor-vremena, predstavlja metriku prostor-vremena, 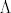 predstavlja kozmolosku konstantu, R predstavlja Riccijev skalar, G je gravitacijska konstanta, a predstavlja kozmolosku konstantu, R predstavlja Riccijev skalar, G je gravitacijska konstanta, a 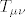 predstavlja tenzor energije-impulsa. u slucaju da je tenzor energije-impulsa jednak 0 i kozmoloska konstanta jednaka 0, onda se jednadzba svodi na vakuumsku jednadzbu predstavlja tenzor energije-impulsa. u slucaju da je tenzor energije-impulsa jednak 0 i kozmoloska konstanta jednaka 0, onda se jednadzba svodi na vakuumsku jednadzbu 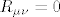 , a u slucaju da je , a u slucaju da je 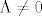 , onda se jednadzba svodi na , onda se jednadzba svodi na 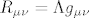 . ovo su trivijalna rjesenja Einsteinovih jedndazbi koje predstavljaju osnovu opce teorije relativnosti. postoje i netrivijalna rjesenja, kao primjerice Schwarzschildova metrika (koja opisuje gravitacijsko polje van neke sferne nerotirajuce mase, tipicno planeta ili crne rupe, ali se moze koristiti za bilo koju takvu nerotirajucu sfernu masu) te primjerice Kerrova metrika koja takodjer opisuje geometriju prostor-vremena oko neke sferne mase. razlika izmedju dva rjesenja jest sto ta masa u slucaju Kerrovog rjesenja rotira. njegovo rjesenje za geometriju prostor-vremena oko sferne mase M koja rotira sa angularnim momentom J se moze napisati u obliku matematicke formule: . ovo su trivijalna rjesenja Einsteinovih jedndazbi koje predstavljaju osnovu opce teorije relativnosti. postoje i netrivijalna rjesenja, kao primjerice Schwarzschildova metrika (koja opisuje gravitacijsko polje van neke sferne nerotirajuce mase, tipicno planeta ili crne rupe, ali se moze koristiti za bilo koju takvu nerotirajucu sfernu masu) te primjerice Kerrova metrika koja takodjer opisuje geometriju prostor-vremena oko neke sferne mase. razlika izmedju dva rjesenja jest sto ta masa u slucaju Kerrovog rjesenja rotira. njegovo rjesenje za geometriju prostor-vremena oko sferne mase M koja rotira sa angularnim momentom J se moze napisati u obliku matematicke formule:
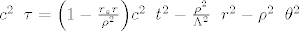 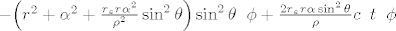
gdje su koordinate 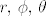 standardne koordinate u sfernom koordinatnom sustavu. a standardne koordinate u sfernom koordinatnom sustavu. a 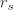 Schwarzschildov radijus Schwarzschildov radijus 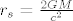 . ostale konstante su tu zbog kraceg zapisa: . ostale konstante su tu zbog kraceg zapisa:
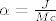 , ,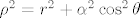 , ,  . .
Kerrova metrika i Kerrovo rjesenje je bitno jer su u realnom slucaju (dakle, u nasem svemiru) crne rupe i opcenito sferne mase koje nemaju rotaciju vrlo rijetke. u tom smislu, Schwarzschildova metrika je samo jako pojednostavljen slucaj. sve crne rupe (koje su i bile jedan od fenomena koje je teorijski pretpostavila opca teorija relativnosti) za koje danas znamo imaju neku kolicinu angularnog momenta, odnosno neku rotaciju.
problem kod rjesenja Einsteinovih jednadzbi jest u tome sto su jednadzbe iznimno nelinearne. u tom smislu, naci egzaktno rjesenje je vrlo tesko, a nekad gotovo i nemoguce. zbog toga, danas se rjesenja Einsteinovih jednadzbi uglavnom izracunavaju pomocu racunalnih simulacija na super-racunalima.
HTH.
btw. ima jako puno o tome na Wikipediiji, pa tko hoce, moze tamo naci dosta odgovora. ovo je, sa stanovista fizike, jos uvijek vrlo zanimljivo podrucje, podrucje koje jos uvijek nije dalo maksimum, kako teorijskog tako i eksperimentalnog, istrazivanja.
|
|
| [Vrh] |
|
Neznalica
Forumaš(ica)

Pridružen/a: 07. 01. 2009. (22:26:13)
Postovi: (6)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 16:25 čet, 8. 1. 2009 Naslov: Re: Rµv-1/2gµvR-λgµv=-8πGTµv Postano: 16:25 čet, 8. 1. 2009 Naslov: Re: Rµv-1/2gµvR-λgµv=-8πGTµv |
    |
|
|
Sto vise od ovoga ocekujes:
[quote="HijenA"]problem kod rjesenja Einsteinovih jednadzbi jest u tome sto su jednadzbe iznimno nelinearne. u tom smislu, naci egzaktno rjesenje je vrlo tesko, a nekad gotovo i nemoguce. zbog toga, danas se rjesenja Einsteinovih jednadzbi uglavnom izracunavaju pomocu racunalnih simulacija na super-racunalima.[/quote]
[quote="zeix"]Da, ovo je Einsteinova jednadzba iz opce teorije relativnosti. Ali da bi je rijesija mora ti biti zadan i ovaj T u jednadzbi. Taj T je tenzor energije-impulsa kolko se ja sicam i on se mora zadati. Npr, za vakum je T=0 pa onda postoji egzaktno rjesenje jednadzbe. Ali ako taj T opisuje nekoliko planeta i asteroida, ona nema sanse da to je rjesis. Drugim rjecima, preaj okladu :D[/quote]
:?:
Dao si zadatak koji ne znas niti sto znaci, ljudi ti lijepo objasne, kazu da bez dodatnih podataka nema rjesenja i ti onda trazis... sto? :roll: Rjesenje za koje bi se odmah dobilo Nobelovu ili kakvu slicnu nagradu? :lol:
Sto vise od ovoga ocekujes:
| HijenA (napisa): | | problem kod rjesenja Einsteinovih jednadzbi jest u tome sto su jednadzbe iznimno nelinearne. u tom smislu, naci egzaktno rjesenje je vrlo tesko, a nekad gotovo i nemoguce. zbog toga, danas se rjesenja Einsteinovih jednadzbi uglavnom izracunavaju pomocu racunalnih simulacija na super-racunalima. |
| zeix (napisa): | Da, ovo je Einsteinova jednadzba iz opce teorije relativnosti. Ali da bi je rijesija mora ti biti zadan i ovaj T u jednadzbi. Taj T je tenzor energije-impulsa kolko se ja sicam i on se mora zadati. Npr, za vakum je T=0 pa onda postoji egzaktno rjesenje jednadzbe. Ali ako taj T opisuje nekoliko planeta i asteroida, ona nema sanse da to je rjesis. Drugim rjecima, preaj okladu  |

Dao si zadatak koji ne znas niti sto znaci, ljudi ti lijepo objasne, kazu da bez dodatnih podataka nema rjesenja i ti onda trazis... sto?  Rjesenje za koje bi se odmah dobilo Nobelovu ili kakvu slicnu nagradu? Rjesenje za koje bi se odmah dobilo Nobelovu ili kakvu slicnu nagradu? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Neznalica
Forumaš(ica)

Pridružen/a: 07. 01. 2009. (22:26:13)
Postovi: (6)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 14:54 pet, 9. 1. 2009 Naslov: Postano: 14:54 pet, 9. 1. 2009 Naslov: |
    |
|
|
Pošto ti nisu rekli da se radi o einsteinovim jednadžbama, možeš se izvuć na to da se radi o algebarskoj jednadžbi [latex]R_{\mu \nu } - \frac{1}
{2}g_{\mu \nu } R - \Lambda g_{\mu \nu } = - 8\pi GT_{\mu \nu }[/latex]. Rješenje je, ovisno o varijabli po kojoj je rješavaš, [latex]R_{\mu \nu } = \frac{1}
{2}g_{\mu \nu } R + \Lambda g_{\mu \nu } - 8\pi GT_{\mu \nu }[/latex] i tak dalje.
Mislim, ak ti neko ne kaže o čem se radi, vjerojatno mu nije bitno, pa riješi za koji god slučaj ti paše.
Pošto ti nisu rekli da se radi o einsteinovim jednadžbama, možeš se izvuć na to da se radi o algebarskoj jednadžbi 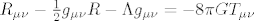 . Rješenje je, ovisno o varijabli po kojoj je rješavaš, . Rješenje je, ovisno o varijabli po kojoj je rješavaš, 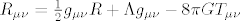 i tak dalje. i tak dalje.
Mislim, ak ti neko ne kaže o čem se radi, vjerojatno mu nije bitno, pa riješi za koji god slučaj ti paše.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Neznalica
Forumaš(ica)

Pridružen/a: 07. 01. 2009. (22:26:13)
Postovi: (6)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
Neznalica
Forumaš(ica)

Pridružen/a: 07. 01. 2009. (22:26:13)
Postovi: (6)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
|














