| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Blah
Forumaš(ica)

Pridružen/a: 11. 09. 2006. (18:07:56)
Postovi: (C1)16
Spol: 
|
|
| [Vrh] |
|
Blah
Forumaš(ica)

Pridružen/a: 11. 09. 2006. (18:07:56)
Postovi: (C1)16
Spol: 
|
 Postano: 16:32 pon, 16. 2. 2009 Naslov: Postano: 16:32 pon, 16. 2. 2009 Naslov: |
    |
|
|
5. zad iz 1.dz-a. Zadana matrica A i baze c=(e1,e1+e2,e1+e2+e3) i d=(e2,e2-e1,e2+e3) i treba naći A(c,d)
E, sad, da li je formula ova A(c,d)=T^-1AS gdje su T matrica od c [111,011,001] i S [0-10,011,001]?
I kaj treba raditi u 10.zad?
5. zad iz 1.dz-a. Zadana matrica A i baze c=(e1,e1+e2,e1+e2+e3) i d=(e2,e2-e1,e2+e3) i treba naći A(c,d)
E, sad, da li je formula ova A(c,d)=T^-1AS gdje su T matrica od c [111,011,001] i S [0-10,011,001]?
I kaj treba raditi u 10.zad?
|
|
| [Vrh] |
|
slash
Forumaš(ica)
Pridružen/a: 20. 02. 2008. (18:17:24)
Postovi: (39)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 15:46 uto, 17. 2. 2009 Naslov: Postano: 15:46 uto, 17. 2. 2009 Naslov: |
    |
|
|
Sve već to ima na forumu riješeno...
[url]http://degiorgi.math.hr/forum/viewtopic.php?t=11975[/url]
Sve već to ima na forumu riješeno...
http://degiorgi.math.hr/forum/viewtopic.php?t=11975
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Blah
Forumaš(ica)

Pridružen/a: 11. 09. 2006. (18:07:56)
Postovi: (C1)16
Spol: 
|
|
| [Vrh] |
|
popravljac
Gost
|
|
| [Vrh] |
|
betty
Forumaš(ica)
Pridružen/a: 23. 02. 2006. (19:17:18)
Postovi: (2D)16
|
|
| [Vrh] |
|
vini
Forumaš(ica)


Pridružen/a: 01. 09. 2006. (18:10:50)
Postovi: (9E)16
Spol: 
|
 Postano: 22:38 sri, 18. 2. 2009 Naslov: Postano: 22:38 sri, 18. 2. 2009 Naslov: |
    |
|
|
Evo ljudi zadace!! Nije cijela,al mislim da ce pomoci.
Nesto sama rjesila,nesto mi pomogli, nesto mi forum pomogao...
7.zadatak nitko ne zna, 1. i 9. nisam se bas potrudila. Ako netko ima volje ispisat,molim vas pisite
[url]http://s568.photobucket.com/albums/ss122/vinkic/vektorski/[/url]
Sretno sutra na popravnom!
Evo ljudi zadace!! Nije cijela,al mislim da ce pomoci.
Nesto sama rjesila,nesto mi pomogli, nesto mi forum pomogao...
7.zadatak nitko ne zna, 1. i 9. nisam se bas potrudila. Ako netko ima volje ispisat,molim vas pisite
http://s568.photobucket.com/albums/ss122/vinkic/vektorski/
Sretno sutra na popravnom!
|
|
| [Vrh] |
|
poravljac
Gost
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 1:21 čet, 19. 2. 2009 Naslov: Postano: 1:21 čet, 19. 2. 2009 Naslov: |
    |
|
|
7. zadatak iz prve zadaće ove godine:
Neka je [latex]\mu_{A}(x)=\sum_{k=0}^{n}a_{k}x^{k}[/latex]. Definiramo [latex]p(x):=\mu_{A}(x+\lambda)=\sum_{k=0}^{n}a_{k}(x+\lambda)^{k}[/latex]. Tada je [latex]p(A-\lambda I)=\sum_{k=0}^{n}a_{k}(A-\lambda I +\lambda I)^{k}=\sum_{k=0}^{n}a_{k}A^{k}=\mu_{A}(A)=0[/latex], a očito je [latex]st(\mu_{A})=st(p)[/latex]. Neka je [latex]q[/latex] neki netrivijalan polinom td [latex]q(A-\lambda I)=0[/latex]. Tada potpuno analogno raspišemo [latex]q[/latex], definiramo [latex]q'(x):=q(x-\lambda)[/latex], i vidi se [latex]q'(A)=0[/latex], pa je [latex]st(q)=st(q') \geq st(\mu_{A})=st(p)[/latex]. Dakle, p je najmanjeg stupnja od svih netrivijalnih polinoma koji poništavaju [latex]A-\lambda I[/latex], i [latex]p[/latex] je očito normiran (jer je [latex]\mu_{A}[/latex] normiran). Slijedi [latex]\mu_{A-\lambda I}(x)=\mu_{A}(x+\lambda)[/latex].
7. zadatak iz prve zadaće ove godine:
Neka je 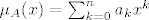 . Definiramo . Definiramo 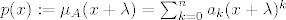 . Tada je . Tada je 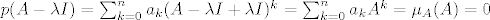 , a očito je , a očito je 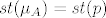 . Neka je . Neka je  neki netrivijalan polinom td neki netrivijalan polinom td 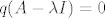 . Tada potpuno analogno raspišemo . Tada potpuno analogno raspišemo  , definiramo , definiramo 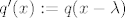 , i vidi se , i vidi se 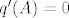 , pa je , pa je 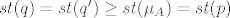 . Dakle, p je najmanjeg stupnja od svih netrivijalnih polinoma koji poništavaju . Dakle, p je najmanjeg stupnja od svih netrivijalnih polinoma koji poništavaju  , i , i  je očito normiran (jer je je očito normiran (jer je 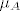 normiran). Slijedi normiran). Slijedi 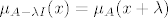 . .
|
|
| [Vrh] |
|
|











