| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
GoranV
Forumaš(ica)

Pridružen/a: 20. 11. 2008. (11:22:01)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:24 uto, 27. 10. 2009 Naslov: Postano: 19:24 uto, 27. 10. 2009 Naslov: |
    |
|
|
[latex]g(x)=\mathrm{th} x[/latex],
[latex]h(x)=x^2-2x+3[/latex].
Tada je [latex]f = h \circ g[/latex], odnosno [latex]f^{-1}\left(\left[3,\, 6\right]\right) = g^{-1}\left(h^{-1}\left(\left[3,\, 6\right]\right)\right)[/latex].
Lako nalazimo da je [latex]h^{-1}\left(\left[3,\, 6\right]\right) = \left[-1,\, 0\right] \cup \left[2,\, 3\right][/latex]. Naime, samo rješimo sustav nejednadžbi [latex]3 \leq x^2 - 2x + 3 \leq 6[/latex], što je ekvivalentno s
[latex]x^2 - 2x \geq 0 \quad \& \quad x^2 - 2x - 3 \leq 0 \quad \Longleftrightarrow[/latex]
[latex]x\left(x-2\right) \geq 0\quad \& \quad \left(x-3\right)\left(x+1\right) \leq 0[/latex].
Sada, [latex]\mathrm{th}[/latex] poprima vrijednosti samo na [latex]\left\langle-1,\, 1\right\rangle[/latex], dakle konačno rješenje je
[latex]g^{-1}\left(\left\langle-1,\, 0\right]\right) = \left\langle-\infty,\, 0\right][/latex].
Valjda je dobro :oops:
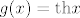 , ,
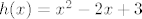 . .
Tada je 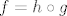 , odnosno , odnosno 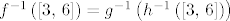 . .
Lako nalazimo da je 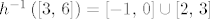 . Naime, samo rješimo sustav nejednadžbi . Naime, samo rješimo sustav nejednadžbi 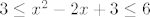 , što je ekvivalentno s , što je ekvivalentno s
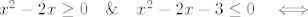
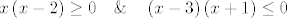 . .
Sada, 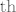 poprima vrijednosti samo na poprima vrijednosti samo na 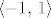 , dakle konačno rješenje je , dakle konačno rješenje je
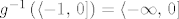 . .
Valjda je dobro 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:30 uto, 27. 10. 2009 Naslov: Postano: 19:30 uto, 27. 10. 2009 Naslov: |
    |
|
|
Preskočit ću traženje praslike kvadratne funkcije i takvih stvari, javi ako treba pomoć :).
Dakle, glavna ideja je da iskoristiš kompoziciju funkcija (o tome smo nadugo i naširoko raspravljali na prethodnoj stranici, tako da ću se suzdržati od toga da to tu ponovim još jednom... ako budeš imao kakvih pitanja, samo reci :)) [latex]f_1(x)=x^2-2x+3[/latex] i [latex]f_2(x)=\tanh x[/latex].
Primijeti da je [latex]f=f_1\circ f_2[/latex], pa je, po pravilu koje znamo, [latex]f^{-1}(A)=f_2^{-1}(f_1^{-1}(A))[/latex]. Kod nas je [latex]A=[3,6][/latex], pa nas prvo zanima kada funkcija [latex]x^2-2x+3[/latex] postiže vrijednosti od [latex]3[/latex] do [latex]6[/latex]. To je sad lako izračunati (i/ili vidjeti s grafa), tu dolazi onaj dio gdje javiš ako ima problema :).
Ako nisam pogriješio, dobijemo da je [latex]f_1^{-1}[3,6]=[-1,0]\cup[2,3][/latex].
Sad, na kraju, želiš vidjeti [latex]f_2^{-1}([-1,0]\cup[2,3])[/latex]. Znamo da je to jednako [latex]f_2^{-1}([-1,0])\cup f_2^{-1}([2,3])[/latex]. Sada ćemo se poslužiti starim trikom i uzeti [url=http://web.math.hr/nastava/analiza/files/formule.pdf]materijale dopuštene na kolokvijima[/url] :D. Naravno, ovo smo mogli i fizički izračunati ili recimo koristiti monotonost, probao sam, uopće nije teško, samo te sad neću time daviti ako već možete imati te formule :).
Uglavnom, bilo kako bilo, dobivamo da je [latex]f_2^{-1}([-1,0])=\langle -\infty,0][/latex], a [latex]f_2^{-1}([2,3])=\emptyset[/latex] (budući da je [latex]\mathcal{R}_{f_2}=\langle -1,1\rangle[/latex]).
Stoga, naše rješenje je [latex]\langle -\infty,0]\cup\emptyset=\langle -\infty,0][/latex].
[size=9]Zapamtit ću ti ovih 30 sekundi, Krijane :P![/size]
Preskočit ću traženje praslike kvadratne funkcije i takvih stvari, javi ako treba pomoć  . .
Dakle, glavna ideja je da iskoristiš kompoziciju funkcija (o tome smo nadugo i naširoko raspravljali na prethodnoj stranici, tako da ću se suzdržati od toga da to tu ponovim još jednom... ako budeš imao kakvih pitanja, samo reci  ) ) 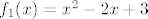 i i 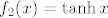 . .
Primijeti da je 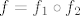 , pa je, po pravilu koje znamo, , pa je, po pravilu koje znamo, 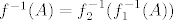 . Kod nas je . Kod nas je 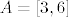 , pa nas prvo zanima kada funkcija , pa nas prvo zanima kada funkcija 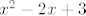 postiže vrijednosti od postiže vrijednosti od 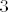 do do  . To je sad lako izračunati (i/ili vidjeti s grafa), tu dolazi onaj dio gdje javiš ako ima problema . To je sad lako izračunati (i/ili vidjeti s grafa), tu dolazi onaj dio gdje javiš ako ima problema  . .
Ako nisam pogriješio, dobijemo da je 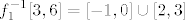 . .
Sad, na kraju, želiš vidjeti 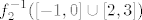 . Znamo da je to jednako . Znamo da je to jednako 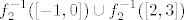 . Sada ćemo se poslužiti starim trikom i uzeti materijale dopuštene na kolokvijima . Sada ćemo se poslužiti starim trikom i uzeti materijale dopuštene na kolokvijima  . Naravno, ovo smo mogli i fizički izračunati ili recimo koristiti monotonost, probao sam, uopće nije teško, samo te sad neću time daviti ako već možete imati te formule . Naravno, ovo smo mogli i fizički izračunati ili recimo koristiti monotonost, probao sam, uopće nije teško, samo te sad neću time daviti ako već možete imati te formule  . .
Uglavnom, bilo kako bilo, dobivamo da je 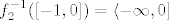 , a , a 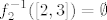 (budući da je (budući da je 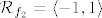 ). ).
Stoga, naše rješenje je 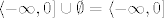 . .
Zapamtit ću ti ovih 30 sekundi, Krijane  ! !
|
|
| [Vrh] |
|
GoranV
Forumaš(ica)

Pridružen/a: 20. 11. 2008. (11:22:01)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:09 sub, 31. 10. 2009 Naslov: Postano: 18:09 sub, 31. 10. 2009 Naslov: |
    |
|
|
[quote="maty321"]koji je inverz funkcije y=-korijen od x, za y<-kor. iz 6, -2kor. iz 2>, x<6,8>
kor. u prijevodu korijen[/quote]
Pretpostavljam da je funkcija [latex]f(x)=-\sqrt{x}[/latex]. Njen inverz je, što si vjerojatno naslutila i bez računanja (jer znaš da je korijen zapravo definiran kao inverz od kvadrata na intervalu [latex][0,+\infty\rangle[/latex]), [latex]f^{-1}(x)=x^2[/latex]. Ne vidim baš što te zbunilo: imaš, kao što si napisala [latex]y=-\sqrt{x}[/latex]. Kvadriraj obje strane i dobiješ [latex]y^2=x[/latex]. I to je to :).
kre5o: Probaj to raspisati po adicijskoj formuli za sinus: [latex]\sin(x-k\pi)=\sin x\cos k\pi-\sin k\pi\cos x[/latex]. Drugi pribrojnik "nestaje" jer je [latex]\sin k\pi=0[/latex] za svaki [latex]k\in\mathbb{Z}[/latex]. Nadalje, [latex]\cos k\pi=(-1)^k[/latex]. (Razmisli malo o tome ako nije jasno: [latex]1=\cos 0=\cos 2\pi=\cos -2\pi=\cos 4\pi=\cos -4\pi=\ldots[/latex], a [latex]-1=\cos \pi=\cos -\pi=\cos 3\pi=\cos -3\pi=\ldots[/latex]. Naravno, za krajnju preciznost, tvrdnju bismo trebali dokazati indukcijom, ali to nije teško... I promise :).)
Dakle, [latex]\sin(x-k\pi)=(-1)^k\sin x[/latex]. Pomnožimo obje strane jednakosti s [latex](-1)^k[/latex] i dobivamo traženu tvrdnju ([latex](-1)^{2k}=1[/latex]).
| maty321 (napisa): | koji je inverz funkcije y=-korijen od x, za y←kor. iz 6, -2kor. iz 2>, x<6,8>
kor. u prijevodu korijen |
Pretpostavljam da je funkcija 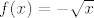 . Njen inverz je, što si vjerojatno naslutila i bez računanja (jer znaš da je korijen zapravo definiran kao inverz od kvadrata na intervalu . Njen inverz je, što si vjerojatno naslutila i bez računanja (jer znaš da je korijen zapravo definiran kao inverz od kvadrata na intervalu 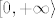 ), ), 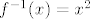 . Ne vidim baš što te zbunilo: imaš, kao što si napisala . Ne vidim baš što te zbunilo: imaš, kao što si napisala 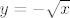 . Kvadriraj obje strane i dobiješ . Kvadriraj obje strane i dobiješ 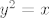 . I to je to . I to je to  . .
kre5o: Probaj to raspisati po adicijskoj formuli za sinus: 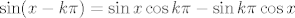 . Drugi pribrojnik "nestaje" jer je . Drugi pribrojnik "nestaje" jer je 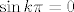 za svaki za svaki 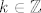 . Nadalje, . Nadalje,  . (Razmisli malo o tome ako nije jasno: . (Razmisli malo o tome ako nije jasno: 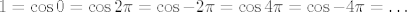 , a , a 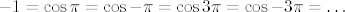 . Naravno, za krajnju preciznost, tvrdnju bismo trebali dokazati indukcijom, ali to nije teško... I promise . Naravno, za krajnju preciznost, tvrdnju bismo trebali dokazati indukcijom, ali to nije teško... I promise  .) .)
Dakle, 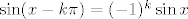 . Pomnožimo obje strane jednakosti s . Pomnožimo obje strane jednakosti s 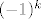 i dobivamo traženu tvrdnju ( i dobivamo traženu tvrdnju (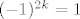 ). ).
Zadnja promjena: mornik; 18:30 sub, 31. 10. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:49 sub, 31. 10. 2009 Naslov: Postano: 19:49 sub, 31. 10. 2009 Naslov: |
    |
|
|
Čuj, pitanje kad se nešto upotrebljava je uvijek malo nezgodno... naravno da se može smisliti zadatak koji će biti specifično namješten da koristi to svojstvo. Što se mene tiče, ja tu činjenicu nisam napamet ni znao dok ju kre5o nije spomenuo :). Naprosto, i ovo očito govorim samo za sebe, ne vidim svrhu da sve moguće činjenice pamtim napamet... kad nešto treba, izvedem to - dosta stvari slijedi samo iz osnova, tj. u ovom slučaju definicija i adicijskih formula.
Dakle, naravno da je ova činjenica korisna, ali sad, reći specifično u kakvim zadacima se upotrebljava... to je po mom mišljenju malo nemoguće :). Naravno, posebno ti je od koristi tamo gdje promatraš ili koristiš periodičnost funkcije, to svakako, ali, kažem, ako zadatak nije baš namješten tako da se koristi ta činjenica, teško je reći gdje se sve može pojaviti.
Čuj, pitanje kad se nešto upotrebljava je uvijek malo nezgodno... naravno da se može smisliti zadatak koji će biti specifično namješten da koristi to svojstvo. Što se mene tiče, ja tu činjenicu nisam napamet ni znao dok ju kre5o nije spomenuo  . Naprosto, i ovo očito govorim samo za sebe, ne vidim svrhu da sve moguće činjenice pamtim napamet... kad nešto treba, izvedem to - dosta stvari slijedi samo iz osnova, tj. u ovom slučaju definicija i adicijskih formula. . Naprosto, i ovo očito govorim samo za sebe, ne vidim svrhu da sve moguće činjenice pamtim napamet... kad nešto treba, izvedem to - dosta stvari slijedi samo iz osnova, tj. u ovom slučaju definicija i adicijskih formula.
Dakle, naravno da je ova činjenica korisna, ali sad, reći specifično u kakvim zadacima se upotrebljava... to je po mom mišljenju malo nemoguće  . Naravno, posebno ti je od koristi tamo gdje promatraš ili koristiš periodičnost funkcije, to svakako, ali, kažem, ako zadatak nije baš namješten tako da se koristi ta činjenica, teško je reći gdje se sve može pojaviti. . Naravno, posebno ti je od koristi tamo gdje promatraš ili koristiš periodičnost funkcije, to svakako, ali, kažem, ako zadatak nije baš namješten tako da se koristi ta činjenica, teško je reći gdje se sve može pojaviti.
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
 Postano: 20:21 sub, 31. 10. 2009 Naslov: Postano: 20:21 sub, 31. 10. 2009 Naslov: |
    |
|
|
Da,i ja raumijem sve to što smo izveli,samo nisam još našla neku svrhu toga u niti jednom zadatku,pa sam mislila da će to možda biti nekakvo teorijsko pitanje..
e i još jedno glupo pitanje, ako imam zadanu funkciju nekakvu,i i nezinu domenu i kodomenu o čega je kodomena čitav R,kako da ispitam jeli surjekcija?
Da,i ja raumijem sve to što smo izveli,samo nisam još našla neku svrhu toga u niti jednom zadatku,pa sam mislila da će to možda biti nekakvo teorijsko pitanje..
e i još jedno glupo pitanje, ako imam zadanu funkciju nekakvu,i i nezinu domenu i kodomenu o čega je kodomena čitav R,kako da ispitam jeli surjekcija?
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
|








