| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
anchi
Gost
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
 Postano: 8:23 čet, 29. 10. 2009 Naslov: Postano: 8:23 čet, 29. 10. 2009 Naslov: |
    |
|
|
evo ja imam rijesene neke zadatke...
nisam 100% sigurna da sve valja, pa ak netko uoci gresku neka me ispravi
1. zadatak :
a) Neka je f1:R^2->R sa f1(x,y)=x^2+y^2-4 (<0)
(p1(x,y)=x, p2=(x,y) su projekcije i one su neprekidne, i umnozak, odnosno zbroj i razlika neprekidnih fukcija su takoder neprekidne funkcije pa je f1 neprekidna funkcija)
praslika od f1 : f1^(-1)=(<-beskonacno,0>) je otvoren (jer je praslika otvorenog skupa pri neprekidnoj fukciji otvoren)
Neka je f2:R^2->R zadana s f2(x,y)=x (>0) je neprekidna i praslika f2^(-1) (<0, + beskonacno>) je otvorena
--> presjek konacne unije otvorenih skupova je otvoren skup
--> A otvoren
b) imas rijesen pod temom 1. kolokvij- zadatak
2. zadatak :
a) skupu S mozemo opisati kuglu (tj. S je podskup od K(0,5))
--> ogranicen je
b)zatvoren skup S je unija cijelog skupa S i njegovih gomislista (S')
->S'={(x,y)element R^2: -1 <=x<=4, y=0} je gomiliste skupa S jer se u svakoj otvorenoj okolini skupa S nalazi barem jedan element skupa S
zatvoren skup S je = S unija S'
c) da bi S bio kompaktan on mora biti omeden i zatvoren. da bi S bio zatvoren mora sadrzavati sva svoja gomilista. iz b) znamo da S ne sadrzi svoja gomilista -- > S nije zatvoren --> S nije kompaktan
4. zadatak : (to mi nije bas najjasnije kak se rijesava... ja sam ovak pokusala al mi je nekak to sumnjivo, pa nek me netko ispravi)
Neka nam je A={(x,y) element R^2: y=1, x<1}, A'={(x,y) element R^2: y=1, x<=1}.
pitanje je da li je f neprekidna na <-beskonacno, 1]?
--> f je neprekidna na <-beskonacno, 1>, jos trebamo provjeriti za tocku (1,1)
lim(x->1)f(x)=1 =!=0=f(1) pa f nije neprekidna
5. zadatak :
a) A pravi podskup od K je zatvoren, jer je f kompakta, onda je i omeden, pa je i A omeden --> A kompaktan
--> jer je f neprekidna funkcija --> f(A) kompaktan
b) jer je A omeden i zatvoren, a f neprekidna -- > da
c) da, jer je u oba slucaja A omeden i f je neprekidna funkcija
eto... to su moja rijesenja. ako netko vidi gresku neka ispravi...
i ako moj 4. zad. ipak nije tocan da ga raspise :) i 5.b) takoder...
evo ja imam rijesene neke zadatke...
nisam 100% sigurna da sve valja, pa ak netko uoci gresku neka me ispravi
1. zadatak :
a) Neka je f1:R^2->R sa f1(x,y)=x^2+y^2-4 (<0)
(p1(x,y)=x, p2=(x,y) su projekcije i one su neprekidne, i umnozak, odnosno zbroj i razlika neprekidnih fukcija su takoder neprekidne funkcije pa je f1 neprekidna funkcija)
praslika od f1 : f1^(-1)=(<-beskonacno,0>) je otvoren (jer je praslika otvorenog skupa pri neprekidnoj fukciji otvoren)
Neka je f2:R^2->R zadana s f2(x,y)=x (>0) je neprekidna i praslika f2^(-1) (<0, + beskonacno>) je otvorena
--> presjek konacne unije otvorenih skupova je otvoren skup
--> A otvoren
b) imas rijesen pod temom 1. kolokvij- zadatak
2. zadatak :
a) skupu S mozemo opisati kuglu (tj. S je podskup od K(0,5))
--> ogranicen je
b)zatvoren skup S je unija cijelog skupa S i njegovih gomislista (S')
->S'={(x,y)element R^2: -1 <=x<=4, y=0} je gomiliste skupa S jer se u svakoj otvorenoj okolini skupa S nalazi barem jedan element skupa S
zatvoren skup S je = S unija S'
c) da bi S bio kompaktan on mora biti omeden i zatvoren. da bi S bio zatvoren mora sadrzavati sva svoja gomilista. iz b) znamo da S ne sadrzi svoja gomilista -- > S nije zatvoren --> S nije kompaktan
4. zadatak : (to mi nije bas najjasnije kak se rijesava... ja sam ovak pokusala al mi je nekak to sumnjivo, pa nek me netko ispravi)
Neka nam je A={(x,y) element R^2: y=1, x<1}, A'={(x,y) element R^2: y=1, x<=1}.
pitanje je da li je f neprekidna na <-beskonacno, 1]?
--> f je neprekidna na <-beskonacno, 1>, jos trebamo provjeriti za tocku (1,1)
lim(x->1)f(x)=1 =!=0=f(1) pa f nije neprekidna
5. zadatak :
a) A pravi podskup od K je zatvoren, jer je f kompakta, onda je i omeden, pa je i A omeden --> A kompaktan
--> jer je f neprekidna funkcija --> f(A) kompaktan
b) jer je A omeden i zatvoren, a f neprekidna -- > da
c) da, jer je u oba slucaja A omeden i f je neprekidna funkcija
eto... to su moja rijesenja. ako netko vidi gresku neka ispravi...
i ako moj 4. zad. ipak nije tocan da ga raspise  i 5.b) takoder... i 5.b) takoder...
|
|
| [Vrh] |
|
s@nj@
Gost
|
|
| [Vrh] |
|
maloka
Forumaš(ica)

Pridružen/a: 05. 02. 2009. (22:00:18)
Postovi: (32)16
|
 Postano: 13:06 sub, 31. 10. 2009 Naslov: Postano: 13:06 sub, 31. 10. 2009 Naslov: |
    |
|
|
Može pomoć oko 5. zad sa kolokvija iz 2007.?
5. a) Neka je K kompaktan u R^n. Da li svaki Cauchyev niz u K konvergira (u K). Što ako K nije kompaktan nego samo zatvoren?
b) Neka je f: [2,3]x[1,2]-> R neprekidna fija. Dostiže li ona nužno minimum na svojoj domeni? Promatrajmo funkciju g=|[2,3]x{3/2} (restrikcija funkcije), postiže li g minimum na svojoj domeni, i gledamo još i fiju h=f|(2,3)x(1,2) (isto restrikcija) postiže li h minimum?
Jel u b) dijelu moram gledat da li je domena kompaktan skup (omeđen i zatvoren) i fija neprekidna onda ona nužno postiže min i max?
Može pomoć oko 5. zad sa kolokvija iz 2007.?
5. a) Neka je K kompaktan u R^n. Da li svaki Cauchyev niz u K konvergira (u K). Što ako K nije kompaktan nego samo zatvoren?
b) Neka je f: [2,3]x[1,2]→ R neprekidna fija. Dostiže li ona nužno minimum na svojoj domeni? Promatrajmo funkciju g=|[2,3]x{3/2} (restrikcija funkcije), postiže li g minimum na svojoj domeni, i gledamo još i fiju h=f|(2,3)x(1,2) (isto restrikcija) postiže li h minimum?
Jel u b) dijelu moram gledat da li je domena kompaktan skup (omeđen i zatvoren) i fija neprekidna onda ona nužno postiže min i max?
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 13:33 sub, 31. 10. 2009 Naslov: Postano: 13:33 sub, 31. 10. 2009 Naslov: |
    |
|
|
pod a): svaki C-niz konvergira u kompaktnom skupu, to mu je i definicija. ak je skup sam zatvoren, onda ako taj niz konvergira, onda mu je limes unutra (u skupu), a C-niz je konvergentan niz pa je onda i u zatvorenom skuu konvergentan (mislim da je tak)
a ovo pod b), dostiže minimum jer je skup kompaktan, a g i h mislim da ne.
pod a): svaki C-niz konvergira u kompaktnom skupu, to mu je i definicija. ak je skup sam zatvoren, onda ako taj niz konvergira, onda mu je limes unutra (u skupu), a C-niz je konvergentan niz pa je onda i u zatvorenom skuu konvergentan (mislim da je tak)
a ovo pod b), dostiže minimum jer je skup kompaktan, a g i h mislim da ne.
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
maloka
Forumaš(ica)

Pridružen/a: 05. 02. 2009. (22:00:18)
Postovi: (32)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 17:25 sub, 31. 10. 2009 Naslov: Postano: 17:25 sub, 31. 10. 2009 Naslov: |
    |
|
|
[quote="maloka"]5. a) Neka je K kompaktan u R^n. Da li svaki Cauchyev niz u K konvergira (u K). Što ako K nije kompaktan nego samo zatvoren?[/quote]
jedna propozicjia je da je skup zatvoren akko je potpun
potpun je ako u njemu svaki C-niz konvergira
dakle ako je kompaktan, onda je zatvoren, pa je potpun, pa u njemu svaki C-niz konvergira
[quote="maloka"]Neka je f: [2,3]x[1,2]-> R neprekidna fija. Dostiže li ona nužno minimum na svojoj domeni?[/quote]
jer je [2,3]x[1,2] kompaktan, jer je zatvoren i ogranicen, po korolaru 7.2, odgovor je da
[quote="maloka"]Promatrajmo funkciju g=f|[2,3]x{3/2} (restrikcija funkcije), postiže li g minimum na svojoj domeni[/quote]
istim razmatranjem kao i prije te uz dodatak da je restrikcija neprekidne funkcije neprekidna, odgovor je da
[quote="maloka"]h=f|(2,3)x(1,2) (isto restrikcija) postiže li h minimum?[/quote]
iako je h neprekidna, domena nije kompaktna, pa je moj odgovor ne nuzno
| maloka (napisa): | | 5. a) Neka je K kompaktan u R^n. Da li svaki Cauchyev niz u K konvergira (u K). Što ako K nije kompaktan nego samo zatvoren? |
jedna propozicjia je da je skup zatvoren akko je potpun
potpun je ako u njemu svaki C-niz konvergira
dakle ako je kompaktan, onda je zatvoren, pa je potpun, pa u njemu svaki C-niz konvergira
| maloka (napisa): | | Neka je f: [2,3]x[1,2]→ R neprekidna fija. Dostiže li ona nužno minimum na svojoj domeni? |
jer je [2,3]x[1,2] kompaktan, jer je zatvoren i ogranicen, po korolaru 7.2, odgovor je da
| maloka (napisa): | | Promatrajmo funkciju g=f|[2,3]x{3/2} (restrikcija funkcije), postiže li g minimum na svojoj domeni |
istim razmatranjem kao i prije te uz dodatak da je restrikcija neprekidne funkcije neprekidna, odgovor je da
| maloka (napisa): | | h=f|(2,3)x(1,2) (isto restrikcija) postiže li h minimum? |
iako je h neprekidna, domena nije kompaktna, pa je moj odgovor ne nuzno
_________________
Mario Berljafa
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
babybodom
Forumaš(ica)
Pridružen/a: 29. 06. 2009. (22:03:01)
Postovi: (31)16
Lokacija: zagreb
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
 Postano: 17:46 pon, 2. 11. 2009 Naslov: Postano: 17:46 pon, 2. 11. 2009 Naslov: |
    |
|
|
[b]@ babybodom[/b]
[latex]f(x, y, z) = \frac{xz}{x^2+y^2}ln(x^2+y^2) [/latex]
Problem je u točkama oblika [latex](0,0,z), z \in \mathbb{R}[/latex]. Sve ostalo je prirodna domena. :)
Skup gomilišta je [latex]\mathbb{R}[/latex]
Provjerimo gdje ima limes:
Na području prirodne domene ima limes jer je neprekidna. Za problematične točke uzmimo niz [latex](\frac{1}{n}, \frac{1}{n}, z)[/latex]. Kad uvrstiš uočiš da je limes [latex]\infty[/latex] ukoliko je [latex]z \neq 0[/latex], a ako je [latex]z = 0[/latex] uzmeš niz [latex](\frac{1}{n}, \frac{1}{n}, \frac{1}{n})[/latex] i dobijes također divergenciju.
@ babybodom
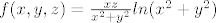
Problem je u točkama oblika 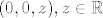 . Sve ostalo je prirodna domena. . Sve ostalo je prirodna domena. 
Skup gomilišta je 
Provjerimo gdje ima limes:
Na području prirodne domene ima limes jer je neprekidna. Za problematične točke uzmimo niz 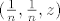 . Kad uvrstiš uočiš da je limes . Kad uvrstiš uočiš da je limes 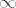 ukoliko je ukoliko je 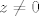 , a ako je , a ako je 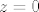 uzmeš niz uzmeš niz 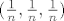 i dobijes također divergenciju. i dobijes također divergenciju.
_________________
reductio ad absurdum
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 18:51 pon, 2. 11. 2009 Naslov: Postano: 18:51 pon, 2. 11. 2009 Naslov: |
    |
|
|
u drugom zadatku iz dve i sedme, jel se dobije da je skup omeđen? mislim, men je ispalo da je to nekakva traka duž x-osi pa nisam baš siguran dal je sve oke
u drugom zadatku iz dve i sedme, jel se dobije da je skup omeđen? mislim, men je ispalo da je to nekakva traka duž x-osi pa nisam baš siguran dal je sve oke
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
 Postano: 21:15 pon, 2. 11. 2009 Naslov: Postano: 21:15 pon, 2. 11. 2009 Naslov: |
    |
|
|
omeden je, ali ti to nije traka na x-osi,
vec unutrasnjos presjeka |x-1| i arctgx, dakle strpas ga u kuglu npr. K((0,0), 1+pi/2)
omeden je, ali ti to nije traka na x-osi,
vec unutrasnjos presjeka |x-1| i arctgx, dakle strpas ga u kuglu npr. K((0,0), 1+pi/2)
|
|
| [Vrh] |
|
babybodom
Forumaš(ica)
Pridružen/a: 29. 06. 2009. (22:03:01)
Postovi: (31)16
Lokacija: zagreb
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
babybodom
Forumaš(ica)
Pridružen/a: 29. 06. 2009. (22:03:01)
Postovi: (31)16
Lokacija: zagreb
|
|
| [Vrh] |
|
|











