| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
 Postano: 17:25 sub, 31. 10. 2009 Naslov: zadaća 2. 2. zadatak - pomoć Postano: 17:25 sub, 31. 10. 2009 Naslov: zadaća 2. 2. zadatak - pomoć |
    |
|
|
Neka je
M = [latex] \{x_{1}, x_{2}, \ldots,x_{n}\in\mathbb{R}^{n}:x_{1}-x_{2}=x_{2}-x_{3}=\ldots=x_{n-1}-x_{n} \} [/latex]. Dokažite da je M potprostor od [latex]R^n[/latex] pa mu odredite jednu bazu i dimenziju.
ja sam taj zadatak sad rješila i dobila da je rješenje baza [latex]\{(1,0,-1,-2,-3,\ldots,2-n), (0,1,2,3,\ldots,n-1)\}[/latex] i dim M=2.
malo mi je to sumnjivo rješenje.. pa bih molila ako je kome volja da proba rješiti taj zad da vidim da li će dobiti isto rješenje...
Neka je
M = 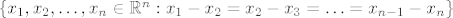 . Dokažite da je M potprostor od . Dokažite da je M potprostor od 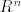 pa mu odredite jednu bazu i dimenziju. pa mu odredite jednu bazu i dimenziju.
ja sam taj zadatak sad rješila i dobila da je rješenje baza 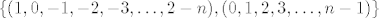 i dim M=2. i dim M=2.
malo mi je to sumnjivo rješenje.. pa bih molila ako je kome volja da proba rješiti taj zad da vidim da li će dobiti isto rješenje...
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 18:11 sub, 31. 10. 2009 Naslov: Postano: 18:11 sub, 31. 10. 2009 Naslov: |
    |
|
|
ovako na prste bi reko da je ok
zasto, pa ocito je dimenzija dva,
npr, ako imas x_1 i x_2 znas cemu su jednake sve one razlike, a onda induktivno dobivas x_3, pa x_4...
ili imas x_1 i znas cemu su jednake one razlike, pa induktivno dobivas x_2, x_3,...
dakle imas dva parametra, pa je dimenzija 2
a ona tvoja dva vektora "su nezavisna", i za njih je ispunjen trazeni uvjet, u smislu, da pripadaju M-u
ovako na prste bi reko da je ok
zasto, pa ocito je dimenzija dva,
npr, ako imas x_1 i x_2 znas cemu su jednake sve one razlike, a onda induktivno dobivas x_3, pa x_4...
ili imas x_1 i znas cemu su jednake one razlike, pa induktivno dobivas x_2, x_3,...
dakle imas dva parametra, pa je dimenzija 2
a ona tvoja dva vektora "su nezavisna", i za njih je ispunjen trazeni uvjet, u smislu, da pripadaju M-u
_________________
Mario Berljafa
|
|
| [Vrh] |
|
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
 Postano: 23:12 pon, 2. 11. 2009 Naslov: Postano: 23:12 pon, 2. 11. 2009 Naslov: |
    |
|
|
[latex]x=x_{1},x_{2},\ldots,x_{n} [/latex]gdje je [latex]x_{1}-x_{2}=x_{2}-x_{3}=\ldots=x_{n-1}-x_{n}[/latex]
i
[latex]y=y_{1},y_{2},\ldots,y_{n} [/latex]gdje je [latex]y_{1}-y_{2}=y_{2}-y_{3}=\ldots=y_{n-1}-y_{n}[/latex]
[latex]z=\alpha x + \beta y[/latex] treba provjertiti da je z element od M
kad to dokažeš onada uzmeš [latex]x\in \ {M}[/latex]
[latex]x_{1}-x_{2}=x_{2}-x_{3}=\ldots=x_{n-1}-x_{n}[/latex]
odnosno
[latex]x_{1}-x_{2}=x_{2}-x_{3}[/latex] povlači [latex]x_{3}=2x_{2}-x_{1}[/latex]
[latex]x_{2}-x_{3}=x_{3}-x_{4}[/latex] povlači
[latex]x_{4}=3x_{2}-2x_{1}[/latex]
itd.
[latex]x_{n}=(n-1)x_{2}-(n-2)x_{1}[/latex]
[latex]x=(x_{1},x_{2},2x_{2}-x_{1},3x_{2}-2x_{1},\ldots,(n-1)x_{2}-(n-2)x_{1})[/latex]
[latex]x=(x_{1}(1,0,-1,-2,-3,\ldots,2-n),x_{2}(0,1,2,3,\ldots, n-1))[/latex]
pa je baza[latex]\{(1,0,-1,-2,-3,\ldots,2-n),(0,1,2,3,\ldots, n-1)\}[/latex]
ja se barem nadam da je to dobro... ako sam pogrješila, molim vas da me ispravite da ne predam krivu zadaću 8)
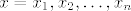 gdje je gdje je 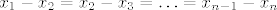
i
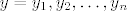 gdje je gdje je 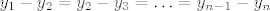
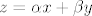 treba provjertiti da je z element od M treba provjertiti da je z element od M
kad to dokažeš onada uzmeš 
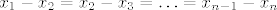
odnosno
 povlači povlači 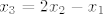
 povlači povlači
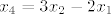
itd.
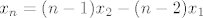
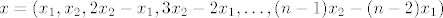
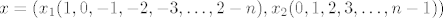
pa je baza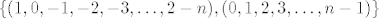
ja se barem nadam da je to dobro... ako sam pogrješila, molim vas da me ispravite da ne predam krivu zadaću 
|
|
| [Vrh] |
|
zekoo
Forumaš(ica)


Pridružen/a: 31. 10. 2009. (22:58:36)
Postovi: (12)16
Spol: 
|
|
| [Vrh] |
|
tp
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (16:46:01)
Postovi: (1F2)16
|
 Postano: 19:16 sri, 4. 11. 2009 Naslov: Postano: 19:16 sri, 4. 11. 2009 Naslov: |
    |
|
|
[quote="zekoo"]imaš taj zadatak u biljeznici, ak si kod pejkovica na vjezbama... :wink:[/quote]
Ovo nije isti zadatak (ako se dobro sjecam).
Na vjezbama smo imali
[latex]x_1-x_2=\cdots=x_{n-1}-x_n=x_n-x_1[/latex],
a ovdje je
[latex]x_1-x_2=\cdots=x_{n-1}-x_n[/latex]
Ovdje je jedna jednadžba manje, pa je i dimenzija 2, a ne 1 kao na vjezbama (naravno, to opcenito ne mora vrijedit, ako npr. dodana jednadzba ne donosi nista novo, usp. npr. [latex]x_1-x_2=x_2-x_3=0[/latex] i [latex]x_1-x_2=x_2-x_3=x_3-x_1=0[/latex])
Inace, u ovdje zadanom zadatku je mozda najlakse nazvati razliku d, a prvi član (x_1) nazvati a, pa cete vidjeti da zapravo imate ... ([size=9]izrezao sam jedan dio jer sam skuzio da vam je to zadaca[/size])
[size=9]Recimo da su ovo bile danasnje konzultacije.[/size]
| zekoo (napisa): | | imaš taj zadatak u biljeznici, ak si kod pejkovica na vjezbama... :wink: |
Ovo nije isti zadatak (ako se dobro sjecam).
Na vjezbama smo imali
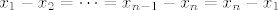 , ,
a ovdje je
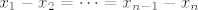
Ovdje je jedna jednadžba manje, pa je i dimenzija 2, a ne 1 kao na vjezbama (naravno, to opcenito ne mora vrijedit, ako npr. dodana jednadzba ne donosi nista novo, usp. npr. 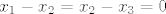 i i 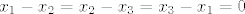 ) )
Inace, u ovdje zadanom zadatku je mozda najlakse nazvati razliku d, a prvi član (x_1) nazvati a, pa cete vidjeti da zapravo imate ... (izrezao sam jedan dio jer sam skuzio da vam je to zadaca)
Recimo da su ovo bile danasnje konzultacije.
|
|
| [Vrh] |
|
zekoo
Forumaš(ica)


Pridružen/a: 31. 10. 2009. (22:58:36)
Postovi: (12)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
 Postano: 15:39 pet, 6. 11. 2009 Naslov: Postano: 15:39 pet, 6. 11. 2009 Naslov: |
    |
|
|
Mislim da je izrezani dio htio reć da imate aritmetički niz x1, x1+d, x1+2d... pa se svaka n-torka može zapisati kao x1(1,1,...,1)+d(0,1,2,...,n-1) pa je to i baza, a dim=2
Mislim da je izrezani dio htio reć da imate aritmetički niz x1, x1+d, x1+2d... pa se svaka n-torka može zapisati kao x1(1,1,...,1)+d(0,1,2,...,n-1) pa je to i baza, a dim=2
|
|
| [Vrh] |
|
zekoo
Forumaš(ica)


Pridružen/a: 31. 10. 2009. (22:58:36)
Postovi: (12)16
Spol: 
|
 Postano: 18:20 pet, 6. 11. 2009 Naslov: Postano: 18:20 pet, 6. 11. 2009 Naslov: |
    |
|
|
[quote="Anonymous"]Mislim da je izrezani dio htio reć da imate aritmetički niz x1, x1+d, x1+2d... pa se svaka n-torka može zapisati kao x1(1,1,...,1)+d(0,1,2,...,n-1) pa je to i baza, a dim=2[/quote]
hvala :D :weee:
| Anonymous (napisa): | | Mislim da je izrezani dio htio reć da imate aritmetički niz x1, x1+d, x1+2d... pa se svaka n-torka može zapisati kao x1(1,1,...,1)+d(0,1,2,...,n-1) pa je to i baza, a dim=2 |
hvala  
|
|
| [Vrh] |
|
ananas182
Forumaš(ica)
Pridružen/a: 07. 11. 2009. (12:25:50)
Postovi: (B)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 13:55 sub, 7. 11. 2009 Naslov: Postano: 13:55 sub, 7. 11. 2009 Naslov: |
    |
|
|
Neka je [latex]A=\left\{ \left( x,y,z\right)\in\mathbb{R}^3|x-z=0\right\}[/latex]
[latex]B=\left\{ \left( x,y,z\right)\in\mathbb{R}^3|x+y+z=0\right\}[/latex]
kako pokazat da se svaki [latex]\left( x,y,z\right)\in\mathbb{R}^3[/latex] moze prikazat kao [latex]\left( x,y,z\right)=\left( x_A,y_A,z_A\right)+\left( x_B,y_B,z_B\right)[/latex] gdje je naravno [latex]\left( x_A,y_A,z_A\right)\in A, \left( x_B,y_B,z_B\right)\in B[/latex]
pa ovako
[latex]\left( x_A,y_A,z_A\right)=\left( x,??,x\right)\in A[/latex]
[latex]\left( x_B,y_B,z_B\right)=\left( 0,??,z-x\right)\notin B[/latex]
[latex]\left( x_B,y_B,z_B\right)=\left( 0,x-z,z-x\right)\in B[/latex]
[latex]\left( x_A,y_A,z_A\right)=\left( x,y-x+z,x\right)\in A[/latex]
Neka je 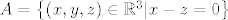
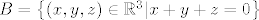
kako pokazat da se svaki 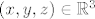 moze prikazat kao moze prikazat kao 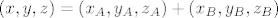 gdje je naravno gdje je naravno 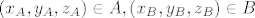
pa ovako
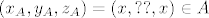
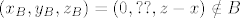
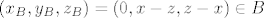
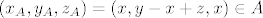
_________________
Mario Berljafa
|
|
| [Vrh] |
|
winks
Forumaš(ica)

Pridružen/a: 14. 10. 2009. (20:14:27)
Postovi: (A)16
|
 Postano: 22:39 uto, 10. 11. 2009 Naslov: zadaća 2. 2. zadatak - pomoć Postano: 22:39 uto, 10. 11. 2009 Naslov: zadaća 2. 2. zadatak - pomoć |
    |
|
|
opet zadaća, :x
zanima me jesam dobro napravila, nekak mi je čudno, pa ako netko ima volje..., :D , hvala,
to je 4. zadatak iz zadaće, uglavnom, ja sam dokazala da su potprostorii dobila sam bazu za L: {(-2, t), (-4, t^2), (-8, t^3)}, i bazu za M: {(-3, t), (-9, t^2), (-27, t^3)}, što znači da su dimenzije i od M i L=3, al meni to ne zvuči baš obećavajuće..., :?
i ja sad nzm nać dim LnM, mislim da prvi, drugi i treći(tj svi iz L) ostaju al skroz se zgubim dalje...,
hvala još jednom..., :wink:
opet zadaća, 
zanima me jesam dobro napravila, nekak mi je čudno, pa ako netko ima volje...,  , hvala, , hvala,
to je 4. zadatak iz zadaće, uglavnom, ja sam dokazala da su potprostorii dobila sam bazu za L: {(-2, t), (-4, t^2), (-8, t^3)}, i bazu za M: {(-3, t), (-9, t^2), (-27, t^3)}, što znači da su dimenzije i od M i L=3, al meni to ne zvuči baš obećavajuće..., 
i ja sad nzm nać dim LnM, mislim da prvi, drugi i treći(tj svi iz L) ostaju al skroz se zgubim dalje...,
hvala još jednom..., 
_________________
opusti se...,
najbolje stvari događaju se kad ih najmanje očekuješ..., =)),
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
 Postano: 1:15 sri, 11. 11. 2009 Naslov: Re: zadaća 2. 2. zadatak - pomoć Postano: 1:15 sri, 11. 11. 2009 Naslov: Re: zadaća 2. 2. zadatak - pomoć |
    |
|
|
[quote="winks"]opet zadaća, :x
to je 4. zadatak iz zadaće, uglavnom, ja sam dokazala da su potprostorii dobila sam bazu za L: {(-2, t), (-4, t^2), (-8, t^3)}, i bazu za M: {(-3, t), (-9, t^2), (-27, t^3)}, što znači da su dimenzije i od M i L=3, al meni to ne zvuči baš obećavajuće..., :?
i ja sad nzm nać dim LnM, mislim da prvi, drugi i treći(tj svi iz L) ostaju al skroz se zgubim dalje...,
hvala još jednom..., :wink:[/quote]
M i L su potprostori od [latex]P_4[/latex] pa za p element od M imamo [latex]p(t)=a+bt+ct^2+dt^3+et^4[/latex] (jer je [latex]dimP_4 = 5[/latex] )
tako da ti je baza od L [latex]\left\{ \left t-2,t^2-4,t^3-8,t^4-16\right\} [/latex]
tako da za bazu L dobiješ 4 vektora,a isto tako i za M.
| winks (napisa): | opet zadaća, 
to je 4. zadatak iz zadaće, uglavnom, ja sam dokazala da su potprostorii dobila sam bazu za L: {(-2, t), (-4, t^2), (-8, t^3)}, i bazu za M: {(-3, t), (-9, t^2), (-27, t^3)}, što znači da su dimenzije i od M i L=3, al meni to ne zvuči baš obećavajuće..., 
i ja sad nzm nać dim LnM, mislim da prvi, drugi i treći(tj svi iz L) ostaju al skroz se zgubim dalje...,
hvala još jednom...,  |
M i L su potprostori od 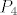 pa za p element od M imamo pa za p element od M imamo 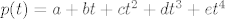 (jer je (jer je 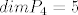 ) )
tako da ti je baza od L 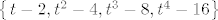
tako da za bazu L dobiješ 4 vektora,a isto tako i za M.
|
|
| [Vrh] |
|
winks
Forumaš(ica)

Pridružen/a: 14. 10. 2009. (20:14:27)
Postovi: (A)16
|
 Postano: 10:39 sri, 11. 11. 2009 Naslov: zadaća 2. 2. zadatak - pomoć Postano: 10:39 sri, 11. 11. 2009 Naslov: zadaća 2. 2. zadatak - pomoć |
    |
|
|
ajmeee..., :oops: ,
skužila, hvala, :D...,
ajmeee...,  , ,
skužila, hvala,  ..., ...,
_________________
opusti se...,
najbolje stvari događaju se kad ih najmanje očekuješ..., =)),
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
|














