| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 20:33 ned, 13. 12. 2009 Naslov: Četvrta i peta zadaća Postano: 20:33 ned, 13. 12. 2009 Naslov: Četvrta i peta zadaća |
    |
|
|
Nije se otvorila ova tema, pa otvaram, možda se ljudi srame ili sve znaju.
U svakom slučaju, mene zanima sljedeće:
Četvrta zadaća, 4. zadatak
[latex]Odredite\ sve\ n \in \mathbb{N}\ za\ koje\ je\ 3^{2n-1}-2^{n-1}\ kvadrat\ nekog\ prirodnog\ broja.[/latex]
Molio bih ideju, vjerojatno onda nije teško provesti.
Nije se otvorila ova tema, pa otvaram, možda se ljudi srame ili sve znaju.
U svakom slučaju, mene zanima sljedeće:
Četvrta zadaća, 4. zadatak

Molio bih ideju, vjerojatno onda nije teško provesti.
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 23:28 uto, 15. 12. 2009 Naslov: Postano: 23:28 uto, 15. 12. 2009 Naslov: |
    |
|
|
prvo pogledas kakav moze uopce bit kvadrat prirodnog broja s obzirom na djeljivost s 4 (i to u 4 slucaja)
I) (4k)^2=16k^2
II) (4k+1)^2=16k^2+8k+1
III) (4k-1)^2=16k^2-8k+1
IV) (4k+2)^2=16k^2+16k+4
iz ovog zakljucujemo da kvadrat prirodnog broja ima ili ostatak 0 pri dijeljenju s 4 (to su slucajevi I, IV) ili ostatak 1 (II,III) (*)
Sad pogledamo ostatak pri dijeljenju broja [latex]3^{2n-1}-2^{n-1}[/latex] s 4
pogledamo po pribrojnicima:
[latex]3^{2n-1}=(4-1)^{2n-1} \equiv (-1)^{2n-1} \equiv -1 (mod 4)[/latex] (**)
Ovo se moze vidjet iz binomnog razvoja [latex](4-1)^{2n-1}[/latex] ali formalno [latex]-1 \equiv (4-1) (mod 4) \Rightarrow (4-1)^{2n-1} \equiv (-1)^{2n-1} (mod 4)[/latex]
Iz (**) dobivamo da [latex]3^{2n-1}=(4-1)^{2n-1}[/latex] daje ostatak -1 pri dijeljenju s 4
Drugi pribrojnik:
[latex]2^{n-1}[/latex] je ocito djeljiv s 4 za svaki n>2,
iz cega onda dobivamo da broj [latex]3^{2n-1}-2^{n-1}[/latex] daje ostatak (-1) pri dijeljenju s 4, pa zbog (*) vidimo da to ne moze biti kvadrat prirodnog broja.
sad su ti ostali samo slucajevi n=1, n=2 koje isprobas na ruke i dobijes da je jedino rjesenje n=2
prvo pogledas kakav moze uopce bit kvadrat prirodnog broja s obzirom na djeljivost s 4 (i to u 4 slucaja)
I) (4k)^2=16k^2
II) (4k+1)^2=16k^2+8k+1
III) (4k-1)^2=16k^2-8k+1
IV) (4k+2)^2=16k^2+16k+4
iz ovog zakljucujemo da kvadrat prirodnog broja ima ili ostatak 0 pri dijeljenju s 4 (to su slucajevi I, IV) ili ostatak 1 (II,III) (*)
Sad pogledamo ostatak pri dijeljenju broja  s 4 s 4
pogledamo po pribrojnicima:
 (**) (**)
Ovo se moze vidjet iz binomnog razvoja 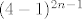 ali formalno ali formalno 
Iz (**) dobivamo da  daje ostatak -1 pri dijeljenju s 4 daje ostatak -1 pri dijeljenju s 4
Drugi pribrojnik:
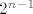 je ocito djeljiv s 4 za svaki n>2, je ocito djeljiv s 4 za svaki n>2,
iz cega onda dobivamo da broj  daje ostatak (-1) pri dijeljenju s 4, pa zbog (*) vidimo da to ne moze biti kvadrat prirodnog broja. daje ostatak (-1) pri dijeljenju s 4, pa zbog (*) vidimo da to ne moze biti kvadrat prirodnog broja.
sad su ti ostali samo slucajevi n=1, n=2 koje isprobas na ruke i dobijes da je jedino rjesenje n=2
|
|
| [Vrh] |
|
Kika123
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (20:20:11)
Postovi: (C)16
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 0:25 čet, 17. 12. 2009 Naslov: Postano: 0:25 čet, 17. 12. 2009 Naslov: |
    |
|
|
kada a i b rastavis na proste faktore, za najvecu zajednicku mjeru za svaki od prostih faktora koji se pojavljuje uzmimas onu manju potenciju s kojom se pojavljuje (ako se neki prosti faktor ne pojavljuje i u a i u b, onda je ona manja potencija = 0), a kod namanjeg zajednickog visekratnika uzimas maksimum od te 2 potencije
tak da posto je min(p_1, p_2) + max(p_1, p_2) = p_1+p_2 slijedi ta formula ( kad pomnozis a i b u umnosku je svaki od prostih faktora na potenciju p_1+p_2)
kada a i b rastavis na proste faktore, za najvecu zajednicku mjeru za svaki od prostih faktora koji se pojavljuje uzmimas onu manju potenciju s kojom se pojavljuje (ako se neki prosti faktor ne pojavljuje i u a i u b, onda je ona manja potencija = 0), a kod namanjeg zajednickog visekratnika uzimas maksimum od te 2 potencije
tak da posto je min(p_1, p_2) + max(p_1, p_2) = p_1+p_2 slijedi ta formula ( kad pomnozis a i b u umnosku je svaki od prostih faktora na potenciju p_1+p_2)
|
|
| [Vrh] |
|
Kika123
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (20:20:11)
Postovi: (C)16
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
 Postano: 16:10 uto, 5. 1. 2010 Naslov: Postano: 16:10 uto, 5. 1. 2010 Naslov: |
    |
|
|
[quote="kikyca"]pitanje, ako kaze da je 2 jednostruka nultocka, to znaci da je to nultocka samo od pocetnog polinoma, a ako je dvosturka da je to nultocka od pocetnog polinoma i njegove prve derivacije?? jesam li dobro skuzila???[/quote]
Da, postoji teorem koji kaze ako je Xo nultočka od f kratnosti k onda je Xo nultočka od f derivirano kratnosti k - 1 . Ta kratnost ustvari znaći sljedeće, ako je nultočka dvostruka kratnost je 2, ako je trostruka kratnost je 3 itd. Isto tako ako je Xo jednostruka nultočka ona ne može biti i nultočka od derivacije jer bi kratnost onda bila k - 1 a k je u ovom slučaju 1.
| kikyca (napisa): | | pitanje, ako kaze da je 2 jednostruka nultocka, to znaci da je to nultocka samo od pocetnog polinoma, a ako je dvosturka da je to nultocka od pocetnog polinoma i njegove prve derivacije?? jesam li dobro skuzila??? |
Da, postoji teorem koji kaze ako je Xo nultočka od f kratnosti k onda je Xo nultočka od f derivirano kratnosti k - 1 . Ta kratnost ustvari znaći sljedeće, ako je nultočka dvostruka kratnost je 2, ako je trostruka kratnost je 3 itd. Isto tako ako je Xo jednostruka nultočka ona ne može biti i nultočka od derivacije jer bi kratnost onda bila k - 1 a k je u ovom slučaju 1.
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 17:20 uto, 5. 1. 2010 Naslov: Postano: 17:20 uto, 5. 1. 2010 Naslov: |
    |
|
|
Evo ti taj isti zadatak rješen pomoću Vietovih formula:
* (za početak mala diskusija): u samom zadatku ti veli da su sva rješenja realna, pa vrijedi da su nultočke [latex]x_1 = 2, x_2 = x_3[/latex].
Iz Vietovih formula znamo:
[latex]x_1+x_2+x_3 = -a_{n-1}\\
x_1x_2+x_2x_3+x_1x_3 = a_{n-2}\\
x_1x_2x_3=-a_{n-3}[/latex]
Polinom je [latex]p(x)=x^3+ax+b[/latex], pa iz toga čitamo [latex]a_{n-1}=0, a_{n-2}=a, a_{n-3}=b[/latex] i to uvrstimo u Vietove formule (i imamo na umu da je [latex]x_2=x_3[/latex]).
[latex]2+2x_2 = 0 \rightarrow x_2 = -1[/latex]
Dobili smo da je druga nultočka (ona dvostruka) [latex]x_2=x_3=-1[/latex], pa nastavljamo sa Vietovim formulama:
[latex]2 \cdot (-1) + (-1) \cdot (-1) + 2 \cdot (-1) = a \rightarrow a = -3 \\
2 \cdot (-1) \cdot (-1) = -b \rightarrow b = -2[/latex].
Konačno: polinom je [latex]p(x)=x^3-3x-2[/latex]
Možeš se još dodatno uvjeriti da je rastav tog polinoma zbilja [latex](x+1)^2(x-2)[/latex] ili ukucaš polinom u WolframAlpha i vidiš da je to rješenje točno. ;)
Evo ti taj isti zadatak rješen pomoću Vietovih formula:
* (za početak mala diskusija): u samom zadatku ti veli da su sva rješenja realna, pa vrijedi da su nultočke 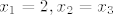 . .
Iz Vietovih formula znamo:
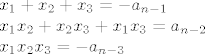
Polinom je 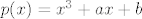 , pa iz toga čitamo , pa iz toga čitamo  i to uvrstimo u Vietove formule (i imamo na umu da je i to uvrstimo u Vietove formule (i imamo na umu da je 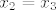 ). ).
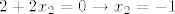
Dobili smo da je druga nultočka (ona dvostruka) 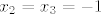 , pa nastavljamo sa Vietovim formulama: , pa nastavljamo sa Vietovim formulama:
 . .
Konačno: polinom je 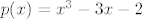
Možeš se još dodatno uvjeriti da je rastav tog polinoma zbilja 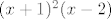 ili ukucaš polinom u WolframAlpha i vidiš da je to rješenje točno. ili ukucaš polinom u WolframAlpha i vidiš da je to rješenje točno. 
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
 Postano: 12:03 sri, 6. 1. 2010 Naslov: Postano: 12:03 sri, 6. 1. 2010 Naslov: |
    |
|
|
[quote="kenny"]Evo ti taj isti zadatak rješen pomoću Vietovih formula:
* (za početak mala diskusija): u samom zadatku ti veli da su sva rješenja realna, pa vrijedi da su nultočke [latex]x_1 = 2, x_2 = x_3[/latex].
Iz Vietovih formula znamo:
[latex]x_1+x_2+x_3 = -a_{n-1}\\
x_1x_2+x_2x_3+x_1x_3 = a_{n-2}\\
x_1x_2x_3=-a_{n-3}[/latex]
Polinom je [latex]p(x)=x^3+ax+b[/latex], pa iz toga čitamo [latex]a_{n-1}=0, a_{n-2}=a, a_{n-3}=b[/latex] i to uvrstimo u Vietove formule (i imamo na umu da je [latex]x_2=x_3[/latex]).
[latex]2+2x_2 = 0 \rightarrow x_2 = -1[/latex]
Dobili smo da je druga nultočka (ona dvostruka) [latex]x_2=x_3=-1[/latex], pa nastavljamo sa Vietovim formulama:
[latex]2 \cdot (-1) + (-1) \cdot (-1) + 2 \cdot (-1) = a \rightarrow a = -3 \\
2 \cdot (-1) \cdot (-1) = -b \rightarrow b = -2[/latex].
Konačno: polinom je [latex]p(x)=x^3-3x-2[/latex]
Možeš se još dodatno uvjeriti da je rastav tog polinoma zbilja [latex](x+1)^2(x-2)[/latex] ili ukucaš polinom u WolframAlpha i vidiš da je to rješenje točno. ;)[/quote]
Lijepo. Ovo je puno elegantnije rješenje.
| kenny (napisa): | Evo ti taj isti zadatak rješen pomoću Vietovih formula:
* (za početak mala diskusija): u samom zadatku ti veli da su sva rješenja realna, pa vrijedi da su nultočke 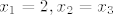 . .
Iz Vietovih formula znamo:
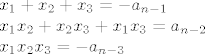
Polinom je 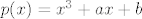 , pa iz toga čitamo , pa iz toga čitamo  i to uvrstimo u Vietove formule (i imamo na umu da je i to uvrstimo u Vietove formule (i imamo na umu da je 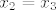 ). ).
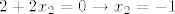
Dobili smo da je druga nultočka (ona dvostruka) 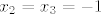 , pa nastavljamo sa Vietovim formulama: , pa nastavljamo sa Vietovim formulama:
 . .
Konačno: polinom je 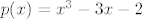
Možeš se još dodatno uvjeriti da je rastav tog polinoma zbilja 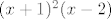 ili ukucaš polinom u WolframAlpha i vidiš da je to rješenje točno. ili ukucaš polinom u WolframAlpha i vidiš da je to rješenje točno.  |
Lijepo. Ovo je puno elegantnije rješenje.
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
|














