| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:37 pon, 7. 12. 2009 Naslov: Postano: 21:37 pon, 7. 12. 2009 Naslov: |
    |
|
|
Ne preostaje ti ništa nego da probaš ponovo. :)
(Drugim riječima, provjerio sam sad za svaki slučaj ručno upravo taj postupak kojim (mislim da) si išla i to je sasvim u redu postupak, dobije se dosta lagano rješenje - konačan broj, tako da si vjerojatno samo negdje pogriješila u računu.
Inače, za provjeru takvih stvari je [url=http://www.wolframalpha.com]WolframAlpha[/url] idealan - u ovom slučaju (nasreću :P) ne daje postupak, ali daje sasvim korektno rješenje. Možeš ga direktno i s foruma pozvati, to je zadnja od opcija u onom povećalu koje je nacrtano u meniju na vrhu.)
Ne preostaje ti ništa nego da probaš ponovo. 
(Drugim riječima, provjerio sam sad za svaki slučaj ručno upravo taj postupak kojim (mislim da) si išla i to je sasvim u redu postupak, dobije se dosta lagano rješenje - konačan broj, tako da si vjerojatno samo negdje pogriješila u računu.
Inače, za provjeru takvih stvari je WolframAlpha idealan - u ovom slučaju (nasreću  ) ne daje postupak, ali daje sasvim korektno rješenje. Možeš ga direktno i s foruma pozvati, to je zadnja od opcija u onom povećalu koje je nacrtano u meniju na vrhu.) ) ne daje postupak, ali daje sasvim korektno rješenje. Možeš ga direktno i s foruma pozvati, to je zadnja od opcija u onom povećalu koje je nacrtano u meniju na vrhu.)
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 19:57 čet, 7. 1. 2010 Naslov: Postano: 19:57 čet, 7. 1. 2010 Naslov: |
    |
|
|
mislim da trebaš gledati samo ovaj niz pod logaritmom, naći njegov minimum i maksimum, i onda, pošto je baza logaritma manja od jedan, on će ih okrenuti, tj, dobit ćeš da je minimum logaritam od maksimuma niza pod logaritmom
mislim da trebaš gledati samo ovaj niz pod logaritmom, naći njegov minimum i maksimum, i onda, pošto je baza logaritma manja od jedan, on će ih okrenuti, tj, dobit ćeš da je minimum logaritam od maksimuma niza pod logaritmom
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 20:46 čet, 7. 1. 2010 Naslov: Postano: 20:46 čet, 7. 1. 2010 Naslov: |
    |
|
|
nultočke ovog čuda su -1 i 8. to je kao neka parabola s otvorom prema gore. maksimum se onda postiže u točki 8 gdje iznosi 72/68 (jednako se dobije i za n = 9, a dalje onda pada). minimalna vrijednost niza je za n = 1 i iznosi 2/5.
mislim da e to to. i onda čitav niz ima minimum log po bazi 1/e od 72/68, a maksimum je ovaj drugi logaritam. to ne moraš znat izračunat kolko je točno
nultočke ovog čuda su -1 i 8. to je kao neka parabola s otvorom prema gore. maksimum se onda postiže u točki 8 gdje iznosi 72/68 (jednako se dobije i za n = 9, a dalje onda pada). minimalna vrijednost niza je za n = 1 i iznosi 2/5.
mislim da e to to. i onda čitav niz ima minimum log po bazi 1/e od 72/68, a maksimum je ovaj drugi logaritam. to ne moraš znat izračunat kolko je točno
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
avicii
Forumaš(ica)

Pridružen/a: 07. 01. 2010. (21:07:05)
Postovi: (3)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 22:16 čet, 7. 1. 2010 Naslov: Postano: 22:16 čet, 7. 1. 2010 Naslov: |
    |
|
|
[quote="avicii"]infinum i supremum - zadatak 3.37
imam skup s = { sin (npi/2)* ((n^2-9)/(5n^2+3n+2)): neN}
inf s=?,sup s=?
bio bi zahvalan na pomoći :) :)[/quote]
rascjepaj na slučajeve, kad je sin(npi/2) 0, 1, -1, u ovisnosti o tome računaj dalje ovaj produkt. npr, za n = 4k+1 je sin(npi/2) = 1, pa sad sa 4k+1 ideš u razlomak. neda mise sad pisat šta treba bit (moram naučit latex više
:oops: ) a ni rješavat. probaj s ovime pa ak zapne, javi. kad riješiš sva tri slučaja, naćeš gomilišta i među njima najveće ti je maksimum, a minimum je najmanje gomilište
| avicii (napisa): | infinum i supremum - zadatak 3.37
imam skup s = { sin (npi/2)* ((n^2-9)/(5n^2+3n+2)): neN}
inf s=?,sup s=?
bio bi zahvalan na pomoći   |
rascjepaj na slučajeve, kad je sin(npi/2) 0, 1, -1, u ovisnosti o tome računaj dalje ovaj produkt. npr, za n = 4k+1 je sin(npi/2) = 1, pa sad sa 4k+1 ideš u razlomak. neda mise sad pisat šta treba bit (moram naučit latex više
 ) a ni rješavat. probaj s ovime pa ak zapne, javi. kad riješiš sva tri slučaja, naćeš gomilišta i među njima najveće ti je maksimum, a minimum je najmanje gomilište ) a ni rješavat. probaj s ovime pa ak zapne, javi. kad riješiš sva tri slučaja, naćeš gomilišta i među njima najveće ti je maksimum, a minimum je najmanje gomilište
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 0:08 pet, 8. 1. 2010 Naslov: Postano: 0:08 pet, 8. 1. 2010 Naslov: |
    |
|
|
u 3.35 skuzis da je ovaj niz (4n^2+1)/(n^2+1) rastuc i omedjen (odozdo ocito s prvim clanom tj. 5/2, a odozgo s 4)
sad vidis pi/2<5/2<4<3pi/2, dakle sve se odvija unutar intervala pi/2,3pi/2
jos imas da je sin neprekidna funkcija padajuca na tom intervalu, pa je sad to ko zad. 3.31 iz dz.
(1)nadjes sup ovog niza (to ce bit limes), sinus od toga je inf skupa
(2)nadjes inf niza (to ce bit prvi clan), sinus od toga je sup skupa
u 3.35 skuzis da je ovaj niz (4n^2+1)/(n^2+1) rastuc i omedjen (odozdo ocito s prvim clanom tj. 5/2, a odozgo s 4)
sad vidis pi/2<5/2<4<3pi/2, dakle sve se odvija unutar intervala pi/2,3pi/2
jos imas da je sin neprekidna funkcija padajuca na tom intervalu, pa je sad to ko zad. 3.31 iz dz.
(1)nadjes sup ovog niza (to ce bit limes), sinus od toga je inf skupa
(2)nadjes inf niza (to ce bit prvi clan), sinus od toga je sup skupa
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 7:33 pet, 8. 1. 2010 Naslov: Postano: 7:33 pet, 8. 1. 2010 Naslov: |
    |
|
|
3.36. je relativno lagan: infimum je očito [latex]0[/latex] budući da su svi članovi pozitivni, a možemo doći proizvoljno blizu [latex]0[/latex] (npr. fiksiramo [latex]m=1[/latex] i neka [latex]n\to +\infty[/latex]). Intuitivno nam je jasno da se najveća vrijednost postiže za male [latex]m[/latex] i [latex]n[/latex]: za [latex]m=n=1[/latex] imamo [latex]\displaystyle \frac{(m+n)^2}{2^{mn}}=2[/latex], dok za [latex]m=2[/latex], [latex]n=1[/latex] (i simetrično) imamo [latex]\displaystyle \frac{(m+n)^2}{2^{mn}}=\frac{9}{4}[/latex].
Pokažimo sada da za sve [latex]m[/latex] i [latex]n[/latex] osim za [latex](m,n)=(2,1)[/latex] i [latex](m,n)=(1,2)[/latex] vrijedi [latex]\displaystyle \frac{(m+n)^2}{2^{mn}}\leq 2[/latex]. Onda će traženi supremum biti [latex]\displaystyle \frac{9}{4}[/latex]. No, to nije teško: [latex](m+n)^2\leq 2^{m+n}[/latex] - to vrijedi jer je [latex]m+n\geq 4[/latex] (za [latex](m,n)=(1,1)[/latex] smo provjerili, a [latex]m+n=3[/latex] smo isključili iz provjere), a znamo da za sve [latex]t\geq 4[/latex] vrijedi [latex]t^2<2^t[/latex].
Stoga je za [latex]m+n\geq 4[/latex], [latex](m+n)^2\leq 2^{m+n}\leq 2^{mn+1}[/latex]. Posljednje vrijedi zato što je [latex]m+n\leq mn+1[/latex] (to je ekvivalentno s [latex](m-1)(n-1)\geq 0[/latex]), a [latex]2^x[/latex] je rastuća funkcija. Dakle, dokazali smo ono što smo željeli i sada znamo da je traženi infimum [latex]0[/latex], a supremum [latex]\displaystyle \frac{9}{4}[/latex].
Što se tiče 3.38., zadatak je dosta teži jer nemamo baš tu intuiciju koju smo imali pri rješavanju prošlog zadatka. Infimum je [latex]1[/latex], a supremum [latex]2[/latex] - niti jedno od toga se ne postiže za [latex]a=b=c[/latex], što je inače relativno uobičajeno kod ovakvih nejednakosti.
Prvo ćemo riješiti infimum: vrijedi [latex]\displaystyle \frac{a}{a+b}>\frac{a}{a+b+c}[/latex] i analogno za ostala tri razlomka. Onda je [latex]\displaystyle \frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}>\frac{a+b+c}{a+b+c}=1[/latex], pa je infimum svakako veći ili jednak [latex]1[/latex]. Preostaje još pokazati da možemo doći proizvoljno blizu [latex]1[/latex].
Uzmimo [latex]a=n[/latex], [latex]b=n^2[/latex] i [latex]c=n^3[/latex] te neka [latex]n\to \infty[/latex]. Tada je [latex]\displaystyle \frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}=\frac{n}{n+n^2}+\frac{n^2}{n^2+n^3}+\frac{n^3}{n^3+n}\to 0+0+1=1[/latex]. Dakle, infimum je zaista [latex]1[/latex].
Sad ćemo supremum dobiti na jedan zbilja nešablonski način - ne znam postoji li nešto jednostavnije, vjerojatno postoji (npr. uzeti [latex]a=n^2[/latex], [latex]b=n[/latex] i [latex]c=n^3[/latex] i onda još pokazati da je upravo limes toga traženi supremum), ali ovo je u svakom slučaju jedna doista zabavna ideja. Neka nam je [latex]\displaystyle f(a,b,c)=\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}[/latex] funkcija koja definira ovaj skup, tj. [latex]S=f(\langle 0,+\infty\rangle\times\langle 0,+\infty\rangle\times\langle 0,+\infty\rangle)[/latex]. Definirajmo funkciju [latex]\displaystyle g(a,b,c)=f(b,a,c)[/latex]. Primijetimo da je [latex]g(\langle 0,+\infty\rangle\times\langle 0,+\infty\rangle\times\langle 0,+\infty\rangle)=f(\langle 0,+\infty\rangle\times\langle 0,+\infty\rangle\times\langle 0,+\infty\rangle)[/latex] - radi se o potpuno istim skupovima, budući da smo samo zamijenili poredak dvije varijable (ako je [latex]t=g(a_0,b_0,c_0)[/latex] za neki [latex](a_0,b_0,c_0)[/latex] onda je [latex]t=f(b_0,a_0,c_0)[/latex] i obrnuto).
Sad kad smo se toga sjetili, stvar je lagana. Primijetimo, naime, da je [latex]\displaystyle f(a,b,c)+g(a,b,c)=\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}+\frac{b}{b+a}+\frac{a}{a+c}+\frac{c}{c+b}=1+1+1=3[/latex]. No, sada je jasno da je supremum [latex]2[/latex]. Naime, prvo pokažimo da je [latex]f(a,b,c)<2[/latex]. Pretpostavimo suprotno: [latex]f(a,b,c)\geq 2[/latex]. Onda je [latex]f(b,a,c)=g(a,b,c)=3-f(a,b,c)\leq 1[/latex], a pokazali smo da je to nemoguće. Nadalje, neka je [latex](a,b,c)[/latex] takav da [latex]f(a,b,c)\to 1[/latex] (pokazali smo gore da takav niz postoji). Onda [latex]g(a,b,c)=f(b,a,c)\to 2[/latex], pa smo pronašli i niz koji ide u [latex]2[/latex], što znači da je supremum upravo [latex]2[/latex].
Kažem, ova dva zadatka nisu pretjerano lagani - zapravo, u 3.36. imamo intuiciju koja nam otprilike govori gdje možemo pronaći taj infimum i supremum, dok u 3.38. toga nemamo. Taj se zadatak, pogotovo drugi dio, može možda, kažem, riješiti i na neki drugi način (makar bi se to vjerojatno opet svelo na isto), ali ovo je zgodan način razmišljanja koji ne zahtijeva baš puno računa.
3.36. je relativno lagan: infimum je očito  budući da su svi članovi pozitivni, a možemo doći proizvoljno blizu budući da su svi članovi pozitivni, a možemo doći proizvoljno blizu  (npr. fiksiramo (npr. fiksiramo 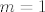 i neka i neka 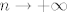 ). Intuitivno nam je jasno da se najveća vrijednost postiže za male ). Intuitivno nam je jasno da se najveća vrijednost postiže za male  i i  : za : za 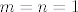 imamo imamo 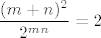 , dok za , dok za 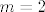 , , 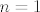 (i simetrično) imamo (i simetrično) imamo 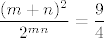 . .
Pokažimo sada da za sve  i i  osim za osim za 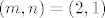 i i 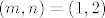 vrijedi vrijedi 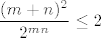 . Onda će traženi supremum biti . Onda će traženi supremum biti  . No, to nije teško: . No, to nije teško: 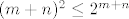 - to vrijedi jer je - to vrijedi jer je 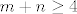 (za (za 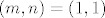 smo provjerili, a smo provjerili, a 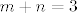 smo isključili iz provjere), a znamo da za sve smo isključili iz provjere), a znamo da za sve 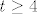 vrijedi vrijedi 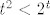 . .
Stoga je za 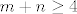 , , 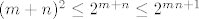 . Posljednje vrijedi zato što je . Posljednje vrijedi zato što je 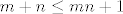 (to je ekvivalentno s (to je ekvivalentno s 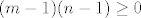 ), a ), a 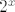 je rastuća funkcija. Dakle, dokazali smo ono što smo željeli i sada znamo da je traženi infimum je rastuća funkcija. Dakle, dokazali smo ono što smo željeli i sada znamo da je traženi infimum  , a supremum , a supremum  . .
Što se tiče 3.38., zadatak je dosta teži jer nemamo baš tu intuiciju koju smo imali pri rješavanju prošlog zadatka. Infimum je  , a supremum , a supremum  - niti jedno od toga se ne postiže za - niti jedno od toga se ne postiže za 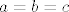 , što je inače relativno uobičajeno kod ovakvih nejednakosti. , što je inače relativno uobičajeno kod ovakvih nejednakosti.
Prvo ćemo riješiti infimum: vrijedi 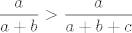 i analogno za ostala tri razlomka. Onda je i analogno za ostala tri razlomka. Onda je 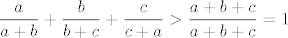 , pa je infimum svakako veći ili jednak , pa je infimum svakako veći ili jednak  . Preostaje još pokazati da možemo doći proizvoljno blizu . Preostaje još pokazati da možemo doći proizvoljno blizu  . .
Uzmimo  , , 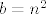 i i 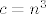 te neka te neka 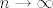 . Tada je . Tada je 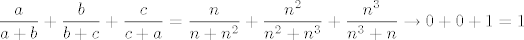 . Dakle, infimum je zaista . Dakle, infimum je zaista  . .
Sad ćemo supremum dobiti na jedan zbilja nešablonski način - ne znam postoji li nešto jednostavnije, vjerojatno postoji (npr. uzeti 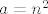 , , 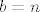 i i 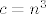 i onda još pokazati da je upravo limes toga traženi supremum), ali ovo je u svakom slučaju jedna doista zabavna ideja. Neka nam je i onda još pokazati da je upravo limes toga traženi supremum), ali ovo je u svakom slučaju jedna doista zabavna ideja. Neka nam je 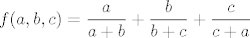 funkcija koja definira ovaj skup, tj. funkcija koja definira ovaj skup, tj. 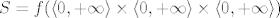 . Definirajmo funkciju . Definirajmo funkciju 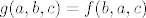 . Primijetimo da je . Primijetimo da je 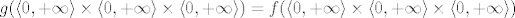 - radi se o potpuno istim skupovima, budući da smo samo zamijenili poredak dvije varijable (ako je - radi se o potpuno istim skupovima, budući da smo samo zamijenili poredak dvije varijable (ako je 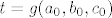 za neki za neki 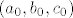 onda je onda je 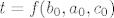 i obrnuto). i obrnuto).
Sad kad smo se toga sjetili, stvar je lagana. Primijetimo, naime, da je 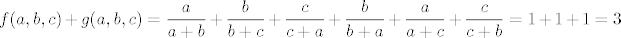 . No, sada je jasno da je supremum . No, sada je jasno da je supremum  . Naime, prvo pokažimo da je . Naime, prvo pokažimo da je 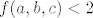 . Pretpostavimo suprotno: . Pretpostavimo suprotno: 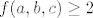 . Onda je . Onda je 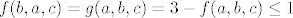 , a pokazali smo da je to nemoguće. Nadalje, neka je , a pokazali smo da je to nemoguće. Nadalje, neka je 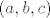 takav da takav da 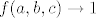 (pokazali smo gore da takav niz postoji). Onda (pokazali smo gore da takav niz postoji). Onda 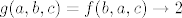 , pa smo pronašli i niz koji ide u , pa smo pronašli i niz koji ide u  , što znači da je supremum upravo , što znači da je supremum upravo  . .
Kažem, ova dva zadatka nisu pretjerano lagani - zapravo, u 3.36. imamo intuiciju koja nam otprilike govori gdje možemo pronaći taj infimum i supremum, dok u 3.38. toga nemamo. Taj se zadatak, pogotovo drugi dio, može možda, kažem, riješiti i na neki drugi način (makar bi se to vjerojatno opet svelo na isto), ali ovo je zgodan način razmišljanja koji ne zahtijeva baš puno računa.
|
|
| [Vrh] |
|
|



















