| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:21 pon, 4. 1. 2010 Naslov: Postano: 23:21 pon, 4. 1. 2010 Naslov: |
    |
|
|
[quote="niveus"]S={sin 4n^2+1/n^2+1: n element N}[/quote]
OK, moram reći... :D
ZAGRADE!!!!!!! (ili još bolje, [latex]LaTeX[/latex] :)) da se zna šta je šta, ovo se može shvatiti na 1001 način:
[latex]\sin{\left(\frac{4n^2+1}{n^2+1}\right)}[/latex],
[latex]\sin{\left(4n^2\right)} + \frac{1}{n^2} + 1[/latex],
[latex]\sin{\left(\frac{4n^2+1}{n^2}\right)} + 1[/latex],
[latex]\sin{\left(4n^2+\frac{1}{n^2+1}\right)}[/latex],
... i još mnogi drugi! :D
@niveus i svi drugi kojima je teško staviti zagrade, ajde molim vas utipkajte još tih 2-4-6 znakova :D da bi vam mogli pomoći, vidite da uvijek ima dobrih ljudi koji rješe (i objasne! kolko tolko) zadatke.
Dajte da bude čitljivo, ovako čovjek izgubi volju ma kolko god dobru namjeru imao. :wink:
P.S. nemojte se ljutiti na mene :oops: :D, ali mislim da sam u pravu ;).
| niveus (napisa): | | S={sin 4n^2+1/n^2+1: n element N} |
OK, moram reći... 
ZAGRADE!!!!!!! (ili još bolje,   ) da se zna šta je šta, ovo se može shvatiti na 1001 način: ) da se zna šta je šta, ovo se može shvatiti na 1001 način:
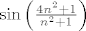 , ,
 , ,
 , ,
 , ,
... i još mnogi drugi! 
@niveus i svi drugi kojima je teško staviti zagrade, ajde molim vas utipkajte još tih 2-4-6 znakova  da bi vam mogli pomoći, vidite da uvijek ima dobrih ljudi koji rješe (i objasne! kolko tolko) zadatke. da bi vam mogli pomoći, vidite da uvijek ima dobrih ljudi koji rješe (i objasne! kolko tolko) zadatke.
Dajte da bude čitljivo, ovako čovjek izgubi volju ma kolko god dobru namjeru imao. 
P.S. nemojte se ljutiti na mene   , ali mislim da sam u pravu , ali mislim da sam u pravu  . .
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:37 pon, 4. 1. 2010 Naslov: Postano: 23:37 pon, 4. 1. 2010 Naslov: |
    |
|
|
Nadam se da je to riječ o 35. zadatku iz vježbi
Naš skup je [latex]S:=\{\sin\frac{4n^2+1}{n^2+1}| n \in \mathbb{N}\}[/latex]
Promatrajmo prvo niz [latex]a_n=\frac{4n^2+1}{n^2+1}=4-\frac{3}{n^2+1}[/latex]. Lagano možemo provjeriti da je niz rastući i omeđen s 4 odozgo, pa je i konvergantan s limesom 4. Iz toga vidimo da je naš niz [latex](a_n)\subseteq[a_1,4>=[\frac{5}{2},4>[/latex].
Sada promatramo niz [latex](\sin(a_n))[/latex]. Iz grafa možemo vidjeti da je funkcija sinus strogopadajuća na intervalu [latex][\frac{5}{2},4>[/latex].
Pa iz toga slijedi [latex]\frac{5}{2}\leq a_n<4 \Rightarrow \sin(\frac{5}{2})\geq sin(a_n)>sin(4), \forrall n \in \mathbb{N} [/latex].
Pa može sljediti da je [latex]\sup(S)=\sin(\frac{5}{2})=\max(S), \inf(S)=\sin(4)[/latex]. Koliko vidim sup je oko 0,6, a inf je oko -0,75.
Nadam se da je to riječ o 35. zadatku iz vježbi
Naš skup je 
Promatrajmo prvo niz  . Lagano možemo provjeriti da je niz rastući i omeđen s 4 odozgo, pa je i konvergantan s limesom 4. Iz toga vidimo da je naš niz . Lagano možemo provjeriti da je niz rastući i omeđen s 4 odozgo, pa je i konvergantan s limesom 4. Iz toga vidimo da je naš niz  . .
Sada promatramo niz  . Iz grafa možemo vidjeti da je funkcija sinus strogopadajuća na intervalu . Iz grafa možemo vidjeti da je funkcija sinus strogopadajuća na intervalu  . .
Pa iz toga slijedi  . .
Pa može sljediti da je  . Koliko vidim sup je oko 0,6, a inf je oko -0,75. . Koliko vidim sup je oko 0,6, a inf je oko -0,75.
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
RazZzoR007
Forumaš(ica)
Pridružen/a: 14. 10. 2009. (22:15:48)
Postovi: (D)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:52 sri, 6. 1. 2010 Naslov: Postano: 21:52 sri, 6. 1. 2010 Naslov: |
    |
|
|
Glavna ideja kod ovog zadatka je uzeti onu tablicu s limesima i isprobavati sve limese po redu :lol: (šalim se, naravno, bilo bi lijepo da odmah znamo koji bi nam poznati limesi mogli biti povezani s ovim zadatkom, da ne moramo isprobavati bar sve i da otprilike znamo kako bi rješenje trebalo ići :)). Bilo kako bilo, imamo sreće, pa se čini zapravo samo jedan limes ima neke direktne veze s kotangensom - idemo, dakle, imamo li kakve koristi od [latex]\displaystyle \lim_{x\rightarrow 0}\frac{\sin x}{x}=1[/latex] :D. Zapravo, mislim da je ovo sasvim dovoljno velik hint, pa nemoj nizaboga čitati dalje :P.
Primijetimo da je [latex]\displaystyle \cot^2 x\cdot (1-\cos^4 x)=\frac{\cos^2 x}{\sin^2 x}\cdot (1-\cos^2 x)(1+\cos^2 x)[/latex]. Možemo raspisati još jedan korak, tj. dobiti [latex]\displaystyle \frac{\cos^2 x}{\sin^2 x}\cdot (1-\cos x)(1+\cos x)(1+\cos^2 x)[/latex]. Sad imamo neki intuitivni osjećaj da nam [latex]\cos^2 x[/latex] neće smetati, to ide u [latex]1[/latex]. Isto tako, ni s [latex]1+\cos^2 x[/latex] nećemo imati problema, to ide u [latex]2[/latex], kao i [latex]1+\cos x[/latex].
Preostaju [latex]\sin^2 x[/latex] i [latex]1-\cos x[/latex]. No, mi smo mudri (i/ili smo dovoljno dugo pokušavali uklopiti sve moguće limese s papira u ovaj zadatak) :) pa znamo da [latex]\displaystyle \frac{x^2}{\sin^2 x}\to 1[/latex], a i [latex]\displaystyle \frac{1-\cos x}{x^2}\to \frac{1}{2}[/latex].
Sad kad sve to lijepo spojimo, dobivamo da vrijedi [latex]\displaystyle \lim_{x\to 0}\cot^2 x\cdot (1-\cos^4 x)=\lim_{x\to 0} \cos^2 x\cdot \frac{x^2}{\sin^2 x}\cdot \frac{1-\cos x}{x^2}\cdot (1+\cos x)\cdot (1+\cos^2 x)[/latex], a to iznosi [latex]\displaystyle 1\cdot 1\cdot \frac{1}{2}\cdot 2\cdot 2=2[/latex].
[i]A može i tom supstitucijom :D. To je ista stvar, ali ipak ću priznati da ono ipak ljepše izgleda/zvuči :).[/i]
[i]A može i čak još jednostavnije - zapravo, mislim da je ovo [b]uvjerljivo najjednostavniji način[/b] (ovisi, zapravo, na što si ti mislio pod tom supstitucijom :)), bez ikakvih specijalnih limesa: vrijedi [latex]\sin^2 x=1-\cos^2 x[/latex]. Stoga se ti dijelovi u raspisu pokrate i dobijemo da tražimo limes od [latex]\cos^2 x\cdot(1+\cos^2 x)[/latex], što je dakako [latex]1\cdot 2=2[/latex].[/i]
Glavna ideja kod ovog zadatka je uzeti onu tablicu s limesima i isprobavati sve limese po redu  (šalim se, naravno, bilo bi lijepo da odmah znamo koji bi nam poznati limesi mogli biti povezani s ovim zadatkom, da ne moramo isprobavati bar sve i da otprilike znamo kako bi rješenje trebalo ići (šalim se, naravno, bilo bi lijepo da odmah znamo koji bi nam poznati limesi mogli biti povezani s ovim zadatkom, da ne moramo isprobavati bar sve i da otprilike znamo kako bi rješenje trebalo ići  ). Bilo kako bilo, imamo sreće, pa se čini zapravo samo jedan limes ima neke direktne veze s kotangensom - idemo, dakle, imamo li kakve koristi od ). Bilo kako bilo, imamo sreće, pa se čini zapravo samo jedan limes ima neke direktne veze s kotangensom - idemo, dakle, imamo li kakve koristi od   . Zapravo, mislim da je ovo sasvim dovoljno velik hint, pa nemoj nizaboga čitati dalje . Zapravo, mislim da je ovo sasvim dovoljno velik hint, pa nemoj nizaboga čitati dalje  . .
Primijetimo da je 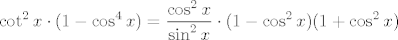 . Možemo raspisati još jedan korak, tj. dobiti . Možemo raspisati još jedan korak, tj. dobiti  . Sad imamo neki intuitivni osjećaj da nam . Sad imamo neki intuitivni osjećaj da nam 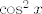 neće smetati, to ide u neće smetati, to ide u  . Isto tako, ni s . Isto tako, ni s  nećemo imati problema, to ide u nećemo imati problema, to ide u  , kao i , kao i  . .
Preostaju 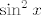 i i  . No, mi smo mudri (i/ili smo dovoljno dugo pokušavali uklopiti sve moguće limese s papira u ovaj zadatak) . No, mi smo mudri (i/ili smo dovoljno dugo pokušavali uklopiti sve moguće limese s papira u ovaj zadatak)  pa znamo da pa znamo da  , a i , a i  . .
Sad kad sve to lijepo spojimo, dobivamo da vrijedi  , a to iznosi , a to iznosi 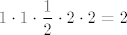 . .
A može i tom supstitucijom  . To je ista stvar, ali ipak ću priznati da ono ipak ljepše izgleda/zvuči . To je ista stvar, ali ipak ću priznati da ono ipak ljepše izgleda/zvuči  . .
A može i čak još jednostavnije - zapravo, mislim da je ovo uvjerljivo najjednostavniji način (ovisi, zapravo, na što si ti mislio pod tom supstitucijom  ), bez ikakvih specijalnih limesa: vrijedi ), bez ikakvih specijalnih limesa: vrijedi  . Stoga se ti dijelovi u raspisu pokrate i dobijemo da tražimo limes od . Stoga se ti dijelovi u raspisu pokrate i dobijemo da tražimo limes od  , što je dakako , što je dakako  . .
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:53 čet, 7. 1. 2010 Naslov: Postano: 21:53 čet, 7. 1. 2010 Naslov: |
    |
|
|
Ti zadaci sa sinusima i kosinusima zbilja nisu toliko teški - svi imaju istu ideju, a onda su sve poslije samo jeftini trikovi 8). Neću ići u detalje budući da mislim da smo ovakve zadatke već rješavali i na forumu (samo potraži malo u najaktivnijim topicima u ovom podforumu u zadnje vrijeme), a puno se rade i na demonstraturama i na vježbama. I naravno, uvijek je korisno napisati dokle si došla/došao, pogotovo u ovo doba prije kolokvija kad ima puno pitanja, a nas par koji koliko-toliko redovito odgovaramo na ovom podforumu nemamo baš vremena da rješavamo svaki zadatak od početka do kraja, naprosto je previše pitanja :).
Dakle, razlikujemo tri (disjunktna) slučaja: [latex]n=2k[/latex], [latex]n=4k-1[/latex], [latex]n=4k-3[/latex], pri čemu je [latex]k\in\mathbb{N}[/latex]. Na ovaj način smo očito pokrili sve mogućnosti, pa je infimum cijelog skupa najmanji od tri infimuma koje dobivamo u ovim skupovima i, analogno, supremum cijelog skupa je najveći od tri supremuma koje dobivamo u tim skupovima.
Prvi i najjednostavniji nam je, dakle, skup [latex]\displaystyle \{\sin(k\pi)\cdot\frac{4k^2-9}{20k^2+6k+2}|k\in\mathbb{N}\}[/latex]. No, kako je sinus od [latex]k\pi[/latex] nužno jednak [latex]0[/latex], cijeli ovaj skup ima samo jedan član: [latex]0[/latex], što je dakako onda i njegov infimum i supremum.
Drugi skup (inače, ovaj drugi i treći skup zapravo možemo promatrati zajedno ne uvlačeći [latex]k[/latex] u cijelu tu priču, što je puno kraće budući da su skupovi jako slični, što će se vidjeti i iz finalnih rezultata, ali ću, jasnoće radi, ipak riješiti svaki skup posebno) je [latex]\displaystyle \{\sin(2k\pi-\frac{1}{2}\pi)\cdot\frac{(4k-1)^2-9}{5(4k-1)^2+3(4k-1)+2}|k\in\mathbb{N}\}[/latex]. To je očito (zbog vrijednosti sinusa) jednako skupu [latex]\displaystyle \{-\frac{4k^2-2k-2}{20k^2-7k+1}|k\in\mathbb{N}\}[/latex]. Dobro, sad pogledamo kad je taj niz rastuć, a kad padajuć. Nisam ručno pokušavao, ali WolframAlpha je uvjeren, a i čini se prirodno da se dobije (kad usporediš član za [latex]k[/latex] i [latex]k+1[/latex]) kvadratna nejednadžba s kojom onda nemaš problema. Ispada da je padajuć "od početka", što znači da je infimum ovog skupa njegov limes u beskonačnosti, a to je očito [latex]\displaystyle -\frac{1}{5}[/latex], a njegov supremum je vrijednost za [latex]k=1[/latex], tj. [latex]0[/latex].
Ostaje nam treći skup: [latex]\displaystyle \{\sin(2k\pi-\frac{3}{2}\pi)\cdot\frac{(4k-3)^2-9}{5(4k-3)^2+3(4k-3)+2}|k\in\mathbb{N}\}[/latex], tj. [latex]\displaystyle \{\frac{8k^2-12k}{40k^2-54k+19}|k\in\mathbb{N}\}[/latex]. Ponovno gledamo kad je ovaj niz rastuć, a kad padajuć - opet se na isti način dobiva kvadratna nejednadžba te ispada da je niz stalno rastuć, što znači da je infimum skupa upravo prvi član pripadajućeg niza, a to je [latex]\displaystyle -\frac{4}{5}[/latex], a supremum je limes u beskonačnosti, tj. [latex]\displaystyle \frac{1}{5}[/latex].
Sad pogledajmo koji je najmanji infimum od tri koja smo spomenuli - to je [latex]\displaystyle -\frac{4}{5}[/latex], dok je najveći supremum [latex]\displaystyle \frac{1}{5}[/latex]. To bi, ako nisam pogriješio :), trebala biti tražena rješenja.
Ti zadaci sa sinusima i kosinusima zbilja nisu toliko teški - svi imaju istu ideju, a onda su sve poslije samo jeftini trikovi  . Neću ići u detalje budući da mislim da smo ovakve zadatke već rješavali i na forumu (samo potraži malo u najaktivnijim topicima u ovom podforumu u zadnje vrijeme), a puno se rade i na demonstraturama i na vježbama. I naravno, uvijek je korisno napisati dokle si došla/došao, pogotovo u ovo doba prije kolokvija kad ima puno pitanja, a nas par koji koliko-toliko redovito odgovaramo na ovom podforumu nemamo baš vremena da rješavamo svaki zadatak od početka do kraja, naprosto je previše pitanja . Neću ići u detalje budući da mislim da smo ovakve zadatke već rješavali i na forumu (samo potraži malo u najaktivnijim topicima u ovom podforumu u zadnje vrijeme), a puno se rade i na demonstraturama i na vježbama. I naravno, uvijek je korisno napisati dokle si došla/došao, pogotovo u ovo doba prije kolokvija kad ima puno pitanja, a nas par koji koliko-toliko redovito odgovaramo na ovom podforumu nemamo baš vremena da rješavamo svaki zadatak od početka do kraja, naprosto je previše pitanja  . .
Dakle, razlikujemo tri (disjunktna) slučaja: 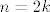 , ,  , ,  , pri čemu je , pri čemu je 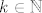 . Na ovaj način smo očito pokrili sve mogućnosti, pa je infimum cijelog skupa najmanji od tri infimuma koje dobivamo u ovim skupovima i, analogno, supremum cijelog skupa je najveći od tri supremuma koje dobivamo u tim skupovima. . Na ovaj način smo očito pokrili sve mogućnosti, pa je infimum cijelog skupa najmanji od tri infimuma koje dobivamo u ovim skupovima i, analogno, supremum cijelog skupa je najveći od tri supremuma koje dobivamo u tim skupovima.
Prvi i najjednostavniji nam je, dakle, skup  . No, kako je sinus od . No, kako je sinus od 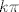 nužno jednak nužno jednak  , cijeli ovaj skup ima samo jedan član: , cijeli ovaj skup ima samo jedan član:  , što je dakako onda i njegov infimum i supremum. , što je dakako onda i njegov infimum i supremum.
Drugi skup (inače, ovaj drugi i treći skup zapravo možemo promatrati zajedno ne uvlačeći  u cijelu tu priču, što je puno kraće budući da su skupovi jako slični, što će se vidjeti i iz finalnih rezultata, ali ću, jasnoće radi, ipak riješiti svaki skup posebno) je u cijelu tu priču, što je puno kraće budući da su skupovi jako slični, što će se vidjeti i iz finalnih rezultata, ali ću, jasnoće radi, ipak riješiti svaki skup posebno) je  . To je očito (zbog vrijednosti sinusa) jednako skupu . To je očito (zbog vrijednosti sinusa) jednako skupu  . Dobro, sad pogledamo kad je taj niz rastuć, a kad padajuć. Nisam ručno pokušavao, ali WolframAlpha je uvjeren, a i čini se prirodno da se dobije (kad usporediš član za . Dobro, sad pogledamo kad je taj niz rastuć, a kad padajuć. Nisam ručno pokušavao, ali WolframAlpha je uvjeren, a i čini se prirodno da se dobije (kad usporediš član za  i i  ) kvadratna nejednadžba s kojom onda nemaš problema. Ispada da je padajuć "od početka", što znači da je infimum ovog skupa njegov limes u beskonačnosti, a to je očito ) kvadratna nejednadžba s kojom onda nemaš problema. Ispada da je padajuć "od početka", što znači da je infimum ovog skupa njegov limes u beskonačnosti, a to je očito 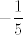 , a njegov supremum je vrijednost za , a njegov supremum je vrijednost za 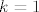 , tj. , tj.  . .
Ostaje nam treći skup:  , tj. , tj.  . Ponovno gledamo kad je ovaj niz rastuć, a kad padajuć - opet se na isti način dobiva kvadratna nejednadžba te ispada da je niz stalno rastuć, što znači da je infimum skupa upravo prvi član pripadajućeg niza, a to je . Ponovno gledamo kad je ovaj niz rastuć, a kad padajuć - opet se na isti način dobiva kvadratna nejednadžba te ispada da je niz stalno rastuć, što znači da je infimum skupa upravo prvi član pripadajućeg niza, a to je  , a supremum je limes u beskonačnosti, tj. , a supremum je limes u beskonačnosti, tj.  . .
Sad pogledajmo koji je najmanji infimum od tri koja smo spomenuli - to je  , dok je najveći supremum , dok je najveći supremum  . To bi, ako nisam pogriješio . To bi, ako nisam pogriješio  , trebala biti tražena rješenja. , trebala biti tražena rješenja.
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ananas
Forumaš(ica)

Pridružen/a: 28. 10. 2009. (17:56:24)
Postovi: (34)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
 Postano: 1:14 sub, 9. 1. 2010 Naslov: Postano: 1:14 sub, 9. 1. 2010 Naslov: |
    |
|
|
Može netko riješit,ako nije problem,4.zadatak,a1 i b, s prošlogodišnjeg kolokvija, 1.grupa. Hvala!! :)
Može netko riješit,ako nije problem,4.zadatak,a1 i b, s prošlogodišnjeg kolokvija, 1.grupa. Hvala!! 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
 Postano: 11:58 sub, 9. 1. 2010 Naslov: Postano: 11:58 sub, 9. 1. 2010 Naslov: |
    |
|
|
Pogledaj malo prijašnje postove, imaš već rješenih primjera :)
[quote="mornik"]Glavna ideja kod ovog zadatka je uzeti onu tablicu s limesima i isprobavati sve limese po redu :lol: (šalim se, naravno, bilo bi lijepo da odmah znamo koji bi nam poznati limesi mogli biti povezani s ovim zadatkom, da ne moramo isprobavati bar sve i da otprilike znamo kako bi rješenje trebalo ići :)). Bilo kako bilo, imamo sreće, pa se čini zapravo samo jedan limes ima neke direktne veze s kotangensom - idemo, dakle, imamo li kakve koristi od [latex]\displaystyle \lim_{x\rightarrow 0}\frac{\sin x}{x}=1[/latex] :D. Zapravo, mislim da je ovo sasvim dovoljno velik hint, pa nemoj nizaboga čitati dalje :P.
Primijetimo da je [latex]\displaystyle \cot^2 x\cdot (1-\cos^4 x)=\frac{\cos^2 x}{\sin^2 x}\cdot (1-\cos^2 x)(1+\cos^2 x)[/latex]. Možemo raspisati još jedan korak, tj. dobiti [latex]\displaystyle \frac{\cos^2 x}{\sin^2 x}\cdot (1-\cos x)(1+\cos x)(1+\cos^2 x)[/latex]. Sad imamo neki intuitivni osjećaj da nam [latex]\cos^2 x[/latex] neće smetati, to ide u [latex]1[/latex]. Isto tako, ni s [latex]1+\cos^2 x[/latex] nećemo imati problema, to ide u [latex]2[/latex], kao i [latex]1+\cos x[/latex].
Preostaju [latex]\sin^2 x[/latex] i [latex]1-\cos x[/latex]. No, mi smo mudri (i/ili smo dovoljno dugo pokušavali uklopiti sve moguće limese s papira u ovaj zadatak) :) pa znamo da [latex]\displaystyle \frac{x^2}{\sin^2 x}\to 1[/latex], a i [latex]\displaystyle \frac{1-\cos x}{x^2}\to \frac{1}{2}[/latex].
Sad kad sve to lijepo spojimo, dobivamo da vrijedi [latex]\displaystyle \lim_{x\to 0}\cot^2 x\cdot (1-\cos^4 x)=\lim_{x\to 0} \cos^2 x\cdot \frac{x^2}{\sin^2 x}\cdot \frac{1-\cos x}{x^2}\cdot (1+\cos x)\cdot (1+\cos^2 x)[/latex], a to iznosi [latex]\displaystyle 1\cdot 1\cdot \frac{1}{2}\cdot 2\cdot 2=2[/latex].
[i]A može i tom supstitucijom :D. To je ista stvar, ali ipak ću priznati da ono ipak ljepše izgleda/zvuči :).[/i]
[i]A može i čak još jednostavnije - zapravo, mislim da je ovo [b]uvjerljivo najjednostavniji način[/b] (ovisi, zapravo, na što si ti mislio pod tom supstitucijom :)), bez ikakvih specijalnih limesa: vrijedi [latex]\sin^2 x=1-\cos^2 x[/latex]. Stoga se ti dijelovi u raspisu pokrate i dobijemo da tražimo limes od [latex]\cos^2 x\cdot(1+\cos^2 x)[/latex], što je dakako [latex]1\cdot 2=2[/latex].[/i][/quote] :)
Pogledaj malo prijašnje postove, imaš već rješenih primjera 
| mornik (napisa): | Glavna ideja kod ovog zadatka je uzeti onu tablicu s limesima i isprobavati sve limese po redu  (šalim se, naravno, bilo bi lijepo da odmah znamo koji bi nam poznati limesi mogli biti povezani s ovim zadatkom, da ne moramo isprobavati bar sve i da otprilike znamo kako bi rješenje trebalo ići (šalim se, naravno, bilo bi lijepo da odmah znamo koji bi nam poznati limesi mogli biti povezani s ovim zadatkom, da ne moramo isprobavati bar sve i da otprilike znamo kako bi rješenje trebalo ići  ). Bilo kako bilo, imamo sreće, pa se čini zapravo samo jedan limes ima neke direktne veze s kotangensom - idemo, dakle, imamo li kakve koristi od ). Bilo kako bilo, imamo sreće, pa se čini zapravo samo jedan limes ima neke direktne veze s kotangensom - idemo, dakle, imamo li kakve koristi od   . Zapravo, mislim da je ovo sasvim dovoljno velik hint, pa nemoj nizaboga čitati dalje . Zapravo, mislim da je ovo sasvim dovoljno velik hint, pa nemoj nizaboga čitati dalje  . .
Primijetimo da je 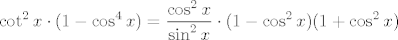 . Možemo raspisati još jedan korak, tj. dobiti . Možemo raspisati još jedan korak, tj. dobiti  . Sad imamo neki intuitivni osjećaj da nam . Sad imamo neki intuitivni osjećaj da nam 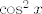 neće smetati, to ide u neće smetati, to ide u  . Isto tako, ni s . Isto tako, ni s  nećemo imati problema, to ide u nećemo imati problema, to ide u  , kao i , kao i  . .
Preostaju 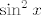 i i  . No, mi smo mudri (i/ili smo dovoljno dugo pokušavali uklopiti sve moguće limese s papira u ovaj zadatak) . No, mi smo mudri (i/ili smo dovoljno dugo pokušavali uklopiti sve moguće limese s papira u ovaj zadatak)  pa znamo da pa znamo da  , a i , a i  . .
Sad kad sve to lijepo spojimo, dobivamo da vrijedi  , a to iznosi , a to iznosi 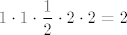 . .
A može i tom supstitucijom  . To je ista stvar, ali ipak ću priznati da ono ipak ljepše izgleda/zvuči . To je ista stvar, ali ipak ću priznati da ono ipak ljepše izgleda/zvuči  . .
A može i čak još jednostavnije - zapravo, mislim da je ovo uvjerljivo najjednostavniji način (ovisi, zapravo, na što si ti mislio pod tom supstitucijom  ), bez ikakvih specijalnih limesa: vrijedi ), bez ikakvih specijalnih limesa: vrijedi  . Stoga se ti dijelovi u raspisu pokrate i dobijemo da tražimo limes od . Stoga se ti dijelovi u raspisu pokrate i dobijemo da tražimo limes od  , što je dakako , što je dakako  . . |

|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 12:03 sub, 9. 1. 2010 Naslov: Postano: 12:03 sub, 9. 1. 2010 Naslov: |
    |
|
|
Evo nekog hintovlja (tj. uglavnom ću probati dati rješenje do na dosadni račun koji ću ostaviti tebi :P), pa probaj znaš li riješiti do kraja - zbilja nije teško, a reci ako bude potrebna još neka pomoć.
[b]2. grupa, 2. b)[/b]
Iskoristi [latex]\displaystyle \ln\frac{a}{b}=\ln a-\ln b[/latex] i [latex]a\ln b=\ln (b^a)[/latex]. Tako ćeš dobiti da se zapravo traži limes od [latex]\displaystyle\ln\frac{n+1}{\sqrt{n^2+1}}[/latex]. Sad možeš iskoristiti da je ln neprekidna funkcija pa "izvući" to iz limesa. Ostaje ti pronaći limes od [latex]\displaystyle\frac{n+1}{\sqrt{n^2+1}}[/latex], što dakako znaš. [latex]ln[/latex]-uješ to i dobivaš limes koji tražiš - iznosi [latex]\ln 1=0[/latex].
[b]2. grupa, 4. a1)[/b]
Dao sam rješenje, štoviše, čak dva i pol različita rješenja :) na ovom topicu nešto ranije, pa pogledaj i reci ako imaš nekih primjedbi. Ovo treće rješenje koje sam spomenuo je uvjerljivo najlakše i zapravo nema nikakve pretjerane veze s traženjem limesa :).
[b]3. grupa, 4. a1)[/b]
Prvo ćemo napisati [latex]\cos x[/latex] kao [latex]1+(\cos(x)-1)[/latex], pri čemu onda [latex]\cos(x)-1[/latex] ide u [latex]0[/latex], što nam se sviđa zbog limesa [latex]\displaystyle\frac{\ln (1+x)}{x}[/latex].
Još ćemo pomnožiti brojnik i nazivnik s [latex]\cos(x)-1[/latex]. Sada imamo da je [latex]\displaystyle \frac{\sin^2 x+x^2}{\ln \cos x})=\frac{(\sin^2 x+x^2)\cdot(\cos(x)-1)}{\ln(1+(\cos(x)-1))\cdot(\cos(x)-1)}[/latex].
Sad ćemo još iz brojnika izlučiti [latex]x^2[/latex], da bi mogli iskoristiti i drugi limes koji nam se tu prirodno javlja: [latex]\displaystyle \frac{\sin x}{x}[/latex].
Dobivamo da je gornji izraz jednak [latex]\displaystyle \frac{(\frac{\sin^2 x}{x^2}+1)\cdot(\cos(x)-1)\cdot x^2}{\ln(1+(\cos(x)-1))\cdot(\cos(x)-1)}[/latex].
Sada smo gotovi - naprosto upari odgovarajuće članove u brojniku i nazivniku da dobiješ željeni limes :). Odgovor bi trebao biti [latex]2\cdot 1\cdot -2=-4[/latex].
[b]4. grupa, 2. b)[/b]
Priča je potpuno ista kao u 2. grupi. Opet pretvori razliku [latex]\ln[/latex]-ova pretvori u [latex]\ln[/latex] razlomka. Nakon toga "izvuci" [latex]\ln[/latex] van limesa, što možeš zbog neprekidnosti, i pronađi limes od [latex]\displaystyle \frac{3^n-n^2}{n^2+5^n}[/latex]. To je [latex]0[/latex], pa je finalni odgovor [latex]-\infty[/latex] (kad broj ide u [latex]0[/latex], [latex]\ln[/latex] tog broja ide u [latex]-\infty[/latex]; možda bi se tu moglo biti nešto formalniji i recimo stvar riješiti preko teorema o sendviču, ali sam poprilično siguran da je i ovo sasvim legalan odgovor :)).
[b]4. grupa, 4. a1)[/b]
Stvar je relativno slična onoj u 3. grupi - opet ćemo pomnožiti i brojnik i nazivnik s [latex]x\sin x[/latex] (što ide u [latex]0[/latex]), da bismo dobili nešto u stilu [latex]\displaystyle\frac{t}{\ln (1+t)}[/latex], čemu limes znamo.
Dobivamo, dakle, [latex]\displaystyle\frac{(1-\cos (2x)+\tan^2 x)(x\sin x)}{(x\sin x)(\ln (1+x\sin x))}[/latex]. Sad ćemo iz brojnika izvaditi [latex]x^2[/latex] (da bismo mogli dobiti još dva poznata limesa - s kosinusom i tangensom) i dobiti [latex]\displaystyle\frac{x^2(4\frac{1-\cos (2x)}{(2x)^2}+\frac{\tan^2 x}{x^2})(x\sin x)}{(x\sin x)(\ln (1+x\sin x))}=\frac{x(4\frac{1-\cos (2x)}{(2x)^2}+\frac{\tan^2 x}{x^2})(x\sin x)}{(\sin x)(\ln (1+x\sin x))}[/latex].
Sad smo gotovi - ponovno ostaje samo uparivanje članova u brojniku i nazivniku. Limes bi, dakle, trebao biti [latex]\displaystyle 1\cdot (4\cdot\frac{1}{2}+1)\cdot 1=3[/latex].
Eto, to bi bilo to, kažem, reci ako trebaju još neka dodatna objašnjenja :).
Evo nekog hintovlja (tj. uglavnom ću probati dati rješenje do na dosadni račun koji ću ostaviti tebi  ), pa probaj znaš li riješiti do kraja - zbilja nije teško, a reci ako bude potrebna još neka pomoć. ), pa probaj znaš li riješiti do kraja - zbilja nije teško, a reci ako bude potrebna još neka pomoć.
2. grupa, 2. b)
Iskoristi  i i  . Tako ćeš dobiti da se zapravo traži limes od . Tako ćeš dobiti da se zapravo traži limes od 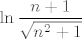 . Sad možeš iskoristiti da je ln neprekidna funkcija pa "izvući" to iz limesa. Ostaje ti pronaći limes od . Sad možeš iskoristiti da je ln neprekidna funkcija pa "izvući" to iz limesa. Ostaje ti pronaći limes od  , što dakako znaš. , što dakako znaš. 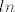 -uješ to i dobivaš limes koji tražiš - iznosi -uješ to i dobivaš limes koji tražiš - iznosi  . .
2. grupa, 4. a1)
Dao sam rješenje, štoviše, čak dva i pol različita rješenja  na ovom topicu nešto ranije, pa pogledaj i reci ako imaš nekih primjedbi. Ovo treće rješenje koje sam spomenuo je uvjerljivo najlakše i zapravo nema nikakve pretjerane veze s traženjem limesa na ovom topicu nešto ranije, pa pogledaj i reci ako imaš nekih primjedbi. Ovo treće rješenje koje sam spomenuo je uvjerljivo najlakše i zapravo nema nikakve pretjerane veze s traženjem limesa  . .
3. grupa, 4. a1)
Prvo ćemo napisati 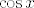 kao kao  , pri čemu onda , pri čemu onda 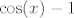 ide u ide u  , što nam se sviđa zbog limesa , što nam se sviđa zbog limesa  . .
Još ćemo pomnožiti brojnik i nazivnik s 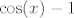 . Sada imamo da je . Sada imamo da je  . .
Sad ćemo još iz brojnika izlučiti 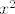 , da bi mogli iskoristiti i drugi limes koji nam se tu prirodno javlja: , da bi mogli iskoristiti i drugi limes koji nam se tu prirodno javlja:  . .
Dobivamo da je gornji izraz jednak  . .
Sada smo gotovi - naprosto upari odgovarajuće članove u brojniku i nazivniku da dobiješ željeni limes  . Odgovor bi trebao biti . Odgovor bi trebao biti  . .
4. grupa, 2. b)
Priča je potpuno ista kao u 2. grupi. Opet pretvori razliku 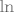 -ova pretvori u -ova pretvori u 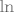 razlomka. Nakon toga "izvuci" razlomka. Nakon toga "izvuci" 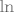 van limesa, što možeš zbog neprekidnosti, i pronađi limes od van limesa, što možeš zbog neprekidnosti, i pronađi limes od  . To je . To je  , pa je finalni odgovor , pa je finalni odgovor 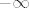 (kad broj ide u (kad broj ide u  , , 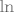 tog broja ide u tog broja ide u 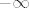 ; možda bi se tu moglo biti nešto formalniji i recimo stvar riješiti preko teorema o sendviču, ali sam poprilično siguran da je i ovo sasvim legalan odgovor ; možda bi se tu moglo biti nešto formalniji i recimo stvar riješiti preko teorema o sendviču, ali sam poprilično siguran da je i ovo sasvim legalan odgovor  ). ).
4. grupa, 4. a1)
Stvar je relativno slična onoj u 3. grupi - opet ćemo pomnožiti i brojnik i nazivnik s 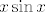 (što ide u (što ide u  ), da bismo dobili nešto u stilu ), da bismo dobili nešto u stilu  , čemu limes znamo. , čemu limes znamo.
Dobivamo, dakle,  . Sad ćemo iz brojnika izvaditi . Sad ćemo iz brojnika izvaditi 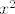 (da bismo mogli dobiti još dva poznata limesa - s kosinusom i tangensom) i dobiti (da bismo mogli dobiti još dva poznata limesa - s kosinusom i tangensom) i dobiti  . .
Sad smo gotovi - ponovno ostaje samo uparivanje članova u brojniku i nazivniku. Limes bi, dakle, trebao biti  . .
Eto, to bi bilo to, kažem, reci ako trebaju još neka dodatna objašnjenja  . .
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 13:43 sub, 9. 1. 2010 Naslov: Postano: 13:43 sub, 9. 1. 2010 Naslov: |
    |
|
|
Odgovor je [latex]\displaystyle \frac{\ln\frac{8}{7}}{\ln\frac{6}{5}}[/latex], a rješenje ide ovako:
Izlučimo [latex]7^x[/latex] iz brojnika i [latex]5^x[/latex] iz nazivnika (u ovom je slučaju potpuno svejedno koji član u brojniku izlučimo, a koji u nazivniku, ovo sam odabrao potpuno nasumično :)). Nakon toga i brojnik i nazivnik podijelimo (tj. pomnožimo, ista stvar) s [latex]x[/latex], da bismo dobili razlomke oblika [latex]\displaystyle \frac{a^x-1}{x}[/latex].
Dobivamo izraz [latex]\displaystyle \frac{7^x}{5^x}\cdot\frac{(\frac{8}{7})^x-1}{x}\cdot\frac{x}{(\frac{6}{5})^x-1}[/latex], a sada limese u svakom od ovih razlomaka znamo odrediti. Dakle, ukupni limes je [latex]\displaystyle \frac{1}{1}\cdot\ln\frac{8}{7}\cdot\frac{1}{\ln\frac{6}{5}}[/latex].
Odgovor je  , a rješenje ide ovako: , a rješenje ide ovako:
Izlučimo  iz brojnika i iz brojnika i  iz nazivnika (u ovom je slučaju potpuno svejedno koji član u brojniku izlučimo, a koji u nazivniku, ovo sam odabrao potpuno nasumično iz nazivnika (u ovom je slučaju potpuno svejedno koji član u brojniku izlučimo, a koji u nazivniku, ovo sam odabrao potpuno nasumično  ). Nakon toga i brojnik i nazivnik podijelimo (tj. pomnožimo, ista stvar) s ). Nakon toga i brojnik i nazivnik podijelimo (tj. pomnožimo, ista stvar) s  , da bismo dobili razlomke oblika , da bismo dobili razlomke oblika  . .
Dobivamo izraz  , a sada limese u svakom od ovih razlomaka znamo odrediti. Dakle, ukupni limes je , a sada limese u svakom od ovih razlomaka znamo odrediti. Dakle, ukupni limes je  . .
|
|
| [Vrh] |
|
|













