| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 22:05 pet, 8. 1. 2010 Naslov: Postano: 22:05 pet, 8. 1. 2010 Naslov: |
    |
|
|
Pretpostavljam da mudro hoćeš neke hintove, a ne potpuna rješenja (makar ovi zadaci zapravo i nemaju puno nekih međukoraka). Dakle,
4.13. a) Ideja je slična kao svugdje gdje se pojavljuju neki viši korijeni - probaj svesti to na razliku/zbroj petih, tj. trećih potencija. Konkretnije - pomnoži i brojnik i nazivnik s [latex]1-\sqrt[5]{x}+\sqrt[5]{x^2}-\sqrt[5]{x^3}+\sqrt[5]{x^4}[/latex], da u brojniku dobiješ [latex]1+x[/latex], a onda pomnoži i brojnik i nazivnik s [latex]1-\sqrt[3]{x}+\sqrt[3]{x^2}[/latex], da i u nazivniku dobiješ [latex]1+x[/latex]. Nakon toga, pokrati ono što se pokratiti da. Limes je [latex]\displaystyle \frac{3}{5}[/latex].
4.14. a) Za veliku većinu [latex]a[/latex] i [latex]b[/latex] ovo nije neodređen oblik, a za ostale (tj. [latex]a[/latex] i [latex]b[/latex] oblika [latex]\displaystyle n+\frac{1}{2}[/latex]) ćeš morati napraviti nešto slično tome što si spomenuo/spomenula - probaj uzeti [latex]t=x-\pi[/latex], to bi ti trebalo olakšati situaciju. Dalje mi se čini da se samo radi o priči s limesom u [latex]0[/latex] i eventualnom gledanju dva slučaja [latex]a[/latex] i [latex]b[/latex].
Inače, [latex]\displaystyle\frac{\sin{ax}}{ax}[/latex] ide u [latex]1[/latex] za [latex]x\to 0[/latex], a u [latex]0[/latex] za [latex]x\to \pm\infty[/latex]. Za ostale [latex]x[/latex] je funkcija neprekidna, tako da znaš što joj je limes.
4.16. c) Probaj uvesti supstituciju [latex]\displaystyle t=x-\frac{\pi}{2}[/latex], pa pogledaj što dobivaš - to bi ti trebalo dosta olakšati zadatak.
4.11. Ne shvaćam o kakvim se supstitucijama radi - to su obični limesi koje ste radili puno puta, samo što idu u [latex]-\infty[/latex], ali to nas ne smeta pretjerano - u prvom zadatku ti je korisno podijeliti i brojnik i nazivnik s [latex]x^3[/latex], pa vidjeti što dobivaš, a u drugom napraviti isto to, samo s [latex]x[/latex]. Treći zadatak ima problem (ili je to namjerno tako zadano) - naime, može li uopće postojati [latex]\sqrt{x}[/latex] koji se pojavljuje u nazivniku, ako [latex]x\rightarrow -\infty[/latex]? :) Dakle, u tom slučaju ne bismo mogli govoriti o limesu funkcije.
Evo, nadam se da je ovo dovoljno hintovlja, pitaj ako treba još :).
EDIT: 4.14. Ne radi se o cjelobrojnim [latex]a[/latex] i [latex]b[/latex], nego o brojevima oblika [latex]\displaystyle n+\frac{1}{2}[/latex], dakako. Pomiješah sinus i kosinus. Moje isprike. :oops:
Pretpostavljam da mudro hoćeš neke hintove, a ne potpuna rješenja (makar ovi zadaci zapravo i nemaju puno nekih međukoraka). Dakle,
4.13. a) Ideja je slična kao svugdje gdje se pojavljuju neki viši korijeni - probaj svesti to na razliku/zbroj petih, tj. trećih potencija. Konkretnije - pomnoži i brojnik i nazivnik s 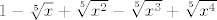 , da u brojniku dobiješ , da u brojniku dobiješ  , a onda pomnoži i brojnik i nazivnik s , a onda pomnoži i brojnik i nazivnik s 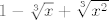 , da i u nazivniku dobiješ , da i u nazivniku dobiješ  . Nakon toga, pokrati ono što se pokratiti da. Limes je . Nakon toga, pokrati ono što se pokratiti da. Limes je  . .
4.14. a) Za veliku većinu  i i 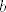 ovo nije neodređen oblik, a za ostale (tj. ovo nije neodređen oblik, a za ostale (tj.  i i 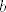 oblika oblika 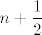 ) ćeš morati napraviti nešto slično tome što si spomenuo/spomenula - probaj uzeti ) ćeš morati napraviti nešto slično tome što si spomenuo/spomenula - probaj uzeti 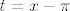 , to bi ti trebalo olakšati situaciju. Dalje mi se čini da se samo radi o priči s limesom u , to bi ti trebalo olakšati situaciju. Dalje mi se čini da se samo radi o priči s limesom u  i eventualnom gledanju dva slučaja i eventualnom gledanju dva slučaja  i i 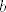 . .
Inače, 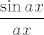 ide u ide u  za za 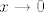 , a u , a u  za za 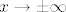 . Za ostale . Za ostale  je funkcija neprekidna, tako da znaš što joj je limes. je funkcija neprekidna, tako da znaš što joj je limes.
4.16. c) Probaj uvesti supstituciju 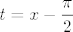 , pa pogledaj što dobivaš - to bi ti trebalo dosta olakšati zadatak. , pa pogledaj što dobivaš - to bi ti trebalo dosta olakšati zadatak.
4.11. Ne shvaćam o kakvim se supstitucijama radi - to su obični limesi koje ste radili puno puta, samo što idu u 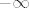 , ali to nas ne smeta pretjerano - u prvom zadatku ti je korisno podijeliti i brojnik i nazivnik s , ali to nas ne smeta pretjerano - u prvom zadatku ti je korisno podijeliti i brojnik i nazivnik s 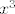 , pa vidjeti što dobivaš, a u drugom napraviti isto to, samo s , pa vidjeti što dobivaš, a u drugom napraviti isto to, samo s  . Treći zadatak ima problem (ili je to namjerno tako zadano) - naime, može li uopće postojati . Treći zadatak ima problem (ili je to namjerno tako zadano) - naime, može li uopće postojati 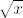 koji se pojavljuje u nazivniku, ako koji se pojavljuje u nazivniku, ako 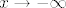 ? ?  Dakle, u tom slučaju ne bismo mogli govoriti o limesu funkcije. Dakle, u tom slučaju ne bismo mogli govoriti o limesu funkcije.
Evo, nadam se da je ovo dovoljno hintovlja, pitaj ako treba još  . .
EDIT: 4.14. Ne radi se o cjelobrojnim  i i 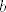 , nego o brojevima oblika , nego o brojevima oblika 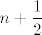 , dakako. Pomiješah sinus i kosinus. Moje isprike. , dakako. Pomiješah sinus i kosinus. Moje isprike. 
Zadnja promjena: mornik; 7:28 sub, 9. 1. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 11:36 sub, 9. 1. 2010 Naslov: Postano: 11:36 sub, 9. 1. 2010 Naslov: |
    |
|
|
U 4.15. c) čini mi se da ti je sve dobro, osim zadnjeg koraka: [latex]\displaystyle \lim_{x\to \infty} x\frac{\sin \frac{\pi}{x}}{\frac{\pi}{x}}\frac{\pi}{x}=1\cdot \pi[/latex], ne [latex]0\cdot \pi[/latex]. Naime, ovaj [latex]\pi[/latex] je jasan, a [latex]\displaystyle \frac{\sin \frac{\pi}{x}}{\frac{\pi}{x}}\to 1[/latex]. Naime, ako [latex]x\to \infty[/latex], [latex]\displaystyle \frac{\pi}{x}\to 0[/latex], pa gledaš limes od [latex]\displaystyle \frac{\sin t}{t}[/latex] u nuli, ne u beskonačnosti :).
U b) dijelu se WolframAlpha slaže [url=http://www.wolframalpha.com/input/?i=limit+of+%28tan+x+-+tan+a%29%2F%28x-a%29%2C+x+to+a][size=9](link)[/size][/url] s tobom :).
U 4.15. c) čini mi se da ti je sve dobro, osim zadnjeg koraka:  , ne , ne 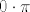 . Naime, ovaj . Naime, ovaj  je jasan, a je jasan, a 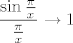 . Naime, ako . Naime, ako 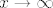 , , 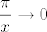 , pa gledaš limes od , pa gledaš limes od 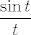 u nuli, ne u beskonačnosti u nuli, ne u beskonačnosti  . .
U b) dijelu se WolframAlpha slaže (link) s tobom  . .
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 14:12 sub, 9. 1. 2010 Naslov: Postano: 14:12 sub, 9. 1. 2010 Naslov: |
    |
|
|
Da, u b) i c) se radi o toj formuli. Budući da ju ja ne znam napamet, išao sam fizički računati (tj. izvoditi ju), što mi je nekako prirodnije jer nema potrebe da moj dementni um pamti išta više nego što je potrebno... :). U svakom slučaju, bilo s tom formulom ili ne, zadaci su dosta lagani - probaj, pa javi ako zapneš. U b) dijelu je odgovor [latex]e^{-1/2}[/latex], a u c) dijelu [latex]e^0=1[/latex].
Pretpostavljam da nećeš cijelo rješenje a) dijela, pa ću probati dati neki koristan hint, makar se teško mogu othrvati tome da riješim cijeli zadatak, ne čini mi se pretjerano lagan ;). Pretpostavljam da je isto [latex]n\in\mathbb{N}[/latex], makar se to [latex]n[/latex] iz nekog razloga uopće ne spominje u uvjetima, ali čini se razumnim. Probaj prikazati pomnožiti brojnik (koji je zapravo [latex]\sqrt[mn]{\cos (\alpha x)^n}-\sqrt[mn]{\cos (\beta x)^m}[/latex]) i nazivnik s [latex]\sqrt[mn]{\cos (\alpha x)^n}^{mn-1}+\sqrt[mn]{\cos (\alpha x)^n}^{mn-2}\sqrt[mn]{\cos (\beta x)^m}+\ldots+\sqrt[mn]{\cos (\beta x)^m}^{mn-1}[/latex], da bismo brojnik učinili mnogo ljepšim (korijeni nikad nisu baš lijepa stvar). Označit ću taj izraz s [latex]T[/latex]. Lagano možeš odrediti limes od [latex]T[/latex], s tim ne bi trebalo biti problema, iznosi [latex]mn[/latex].
Sad imamo da je naš početni izraz jednak[latex]\displaystyle \frac{1}{T}\displaystyle\frac{\cos (\alpha x)^n-\cos (\beta x)^m}{x^2}[/latex]. U ovom trenutku smo manje-više gotovi: napiši brojnik u obliku [latex](\cos(\alpha x)^n-1)-(\cos(\beta x)^m-1)[/latex] i iskoristi da je [latex]x^r-1=(x-1)(x^{r-1}+x^{r-2}\ldots+1)[/latex]. Završni limes bi trebao biti, ako se nisam negdje zeznuo, što je sasvim moguće budući da zadatak nije nimalo trivijalan, [latex]\displaystyle \frac{\beta^2m-\alpha^2n}{2mn}[/latex].
Pitaj ako trebaš pomoć s tim zadatkom, kažem, nije baš računski lagan, tako da je moguće da sam se ja tu negdje zeznuo :oops:.
Da, u b) i c) se radi o toj formuli. Budući da ju ja ne znam napamet, išao sam fizički računati (tj. izvoditi ju), što mi je nekako prirodnije jer nema potrebe da moj dementni um pamti išta više nego što je potrebno...  . U svakom slučaju, bilo s tom formulom ili ne, zadaci su dosta lagani - probaj, pa javi ako zapneš. U b) dijelu je odgovor . U svakom slučaju, bilo s tom formulom ili ne, zadaci su dosta lagani - probaj, pa javi ako zapneš. U b) dijelu je odgovor 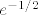 , a u c) dijelu , a u c) dijelu 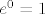 . .
Pretpostavljam da nećeš cijelo rješenje a) dijela, pa ću probati dati neki koristan hint, makar se teško mogu othrvati tome da riješim cijeli zadatak, ne čini mi se pretjerano lagan  . Pretpostavljam da je isto . Pretpostavljam da je isto 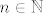 , makar se to , makar se to  iz nekog razloga uopće ne spominje u uvjetima, ali čini se razumnim. Probaj prikazati pomnožiti brojnik (koji je zapravo iz nekog razloga uopće ne spominje u uvjetima, ali čini se razumnim. Probaj prikazati pomnožiti brojnik (koji je zapravo  ) i nazivnik s ) i nazivnik s  , da bismo brojnik učinili mnogo ljepšim (korijeni nikad nisu baš lijepa stvar). Označit ću taj izraz s , da bismo brojnik učinili mnogo ljepšim (korijeni nikad nisu baš lijepa stvar). Označit ću taj izraz s  . Lagano možeš odrediti limes od . Lagano možeš odrediti limes od  , s tim ne bi trebalo biti problema, iznosi , s tim ne bi trebalo biti problema, iznosi 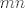 . .
Sad imamo da je naš početni izraz jednak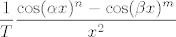 . U ovom trenutku smo manje-više gotovi: napiši brojnik u obliku . U ovom trenutku smo manje-više gotovi: napiši brojnik u obliku  i iskoristi da je i iskoristi da je 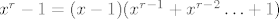 . Završni limes bi trebao biti, ako se nisam negdje zeznuo, što je sasvim moguće budući da zadatak nije nimalo trivijalan, . Završni limes bi trebao biti, ako se nisam negdje zeznuo, što je sasvim moguće budući da zadatak nije nimalo trivijalan, 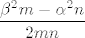 . .
Pitaj ako trebaš pomoć s tim zadatkom, kažem, nije baš računski lagan, tako da je moguće da sam se ja tu negdje zeznuo  . .
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
 Postano: 15:10 sub, 9. 1. 2010 Naslov: Postano: 15:10 sub, 9. 1. 2010 Naslov: |
    |
|
|
[quote="NeonBlack"]http://web.math.hr/nastava/analiza/files/lim2.pdf
Trebala bi mi pomoć oko zadatka 4.27 pod b),riješila sam pod a),ali ovo na treću nikako :? .Hvala.[/quote]
Uglavnom pod a si vjerojatno išla onim oblikom "funkcije na funkciju". Tim se koristiš i u zadatku pod b). A=1, dok je B=+-beskonačno. Trebaš dobiti 1/2, a konačno rješenje je korijen od e. Ne znam latex pa ne mogu napisati detaljno postupak, samo rješenje, sorry :(
| NeonBlack (napisa): | http://web.math.hr/nastava/analiza/files/lim2.pdf
Trebala bi mi pomoć oko zadatka 4.27 pod b),riješila sam pod a),ali ovo na treću nikako  .Hvala. .Hvala. |
Uglavnom pod a si vjerojatno išla onim oblikom "funkcije na funkciju". Tim se koristiš i u zadatku pod b). A=1, dok je B=+-beskonačno. Trebaš dobiti 1/2, a konačno rješenje je korijen od e. Ne znam latex pa ne mogu napisati detaljno postupak, samo rješenje, sorry 
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:25 sub, 9. 1. 2010 Naslov: Postano: 15:25 sub, 9. 1. 2010 Naslov: |
    |
|
|
Zbilja nisu teški zadaci, pa ću samo dati hintove - u prvom samo pomnoži i brojnik i nazivnik s [latex]\pi[/latex] i iskoristi da, ako [latex]x\to 0[/latex], onda i [latex]\pi x\to 0[/latex]. Rješenje je [latex]\displaystyle {\pi}{\ln 10}[/latex]. U drugom iskoristi da vrijedi [latex]\displaystyle \ln (x+2)-\ln 2=\ln(\frac{x}{2}+1)[/latex]. Sad je, primijetit ćeš, taj zadatak gotovo isti kao prvi :). Rješenje je [latex]\frac{1}{2}[/latex].
Reci ako trebaju još neka objašnjenja :).
EDIT: Logaritam po bazi [latex]10[/latex], ne po bazi [latex]e[/latex]. I'm sorry. :)
Zbilja nisu teški zadaci, pa ću samo dati hintove - u prvom samo pomnoži i brojnik i nazivnik s  i iskoristi da, ako i iskoristi da, ako 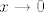 , onda i , onda i 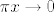 . Rješenje je . Rješenje je  . U drugom iskoristi da vrijedi . U drugom iskoristi da vrijedi 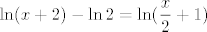 . Sad je, primijetit ćeš, taj zadatak gotovo isti kao prvi . Sad je, primijetit ćeš, taj zadatak gotovo isti kao prvi  . Rješenje je . Rješenje je 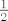 . .
Reci ako trebaju još neka objašnjenja  . .
EDIT: Logaritam po bazi  , ne po bazi , ne po bazi  . I'm sorry. . I'm sorry. 
Zadnja promjena: mornik; 17:19 sub, 9. 1. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
 Postano: 15:40 sub, 9. 1. 2010 Naslov: Postano: 15:40 sub, 9. 1. 2010 Naslov: |
    |
|
|
[quote="ankovacic"]pod 4.13 pod b dobio sam rijesenje (-1), al na vrlo sumnjiv nacin, pa bih molio da me netko obavijesti ako je rijesnje tocno, a ako nije da mi pokaze postupak, unaprijed zahvaljujem.[/quote]
Rješenje ti je krivo, točno je 3/4. uvedi zamjenu t = x+1, onda pomnoži sa (((4. korijen od t) +1) kroz (t^2/3 + t^1/3 + 1)) * ((t^2/3 + t^1/3 + 1) kroz ((4. korijen od t) +1)) i onda ćeš još jednom cijeli izraz množiti sa ((korijen od t) + 1) / ((korijen od t) + 1). Nadam se da ti je postupak jasan...
| ankovacic (napisa): | | pod 4.13 pod b dobio sam rijesenje (-1), al na vrlo sumnjiv nacin, pa bih molio da me netko obavijesti ako je rijesnje tocno, a ako nije da mi pokaze postupak, unaprijed zahvaljujem. |
Rješenje ti je krivo, točno je 3/4. uvedi zamjenu t = x+1, onda pomnoži sa (((4. korijen od t) +1) kroz (t^2/3 + t^1/3 + 1)) * ((t^2/3 + t^1/3 + 1) kroz ((4. korijen od t) +1)) i onda ćeš još jednom cijeli izraz množiti sa ((korijen od t) + 1) / ((korijen od t) + 1). Nadam se da ti je postupak jasan...
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
 Postano: 15:47 sub, 9. 1. 2010 Naslov: Postano: 15:47 sub, 9. 1. 2010 Naslov: |
    |
|
|
[quote="Luuka"][quote="tmarusca"]i kak je rezultat u 4.15. b? meni je [latex]\frac{1}{\cos^2{a}} = \frac{2}{1+\cos{2a}}[/latex]
[/quote]
Ako te ta jednakost muči, to slijedi iz trigonometrijskih identiteta, ne iz limesa ;)
Tu je zapravo formula za polovični kut, koja kaže:
[latex]sin^2 \frac{\alpha}{2}=\frac{1-cos\alpha}{2}[/latex]
[latex]cos^2 \frac{\alpha}{2}=\frac{1+cos\alpha}{2}[/latex]
Ovo su inače jako korisne formule kod računanja integrala, pa ih je korisno imat negdje u glavi :D[/quote]
zahvaljujem na savjetu ali to je jedno rjesenje u dva oblika, naveo sam oba cisto zato da mi netko ne kaze: 'ja sam dobio drukcije', a isto je ;)
@mornik: ne branim ti ja da rijesis cijeli zadatak, slobodno, samo mi ne moras otkriti sve :) ipak je cilj da i ja malo razmisljam (za promjenu) :D
edit:
pretpostavio sam da ce hintovi biti dovoljni da shvatim. i jesu, ali imam jos dva sicusna pitanja:
1. zasto je [latex]\lim{T}= m n[/latex]?
2. sto da radim s tim kosinusima kad ih tak faktoriziram?? nisam nasao neku formulu ili nesto...
ovo je sve naravno pod pretpostavkom da si za [latex]\cos(\alpha x)^n [/latex] mislio [latex] {\cos^n(\alpha x)}[/latex]. :)
| Luuka (napisa): | | tmarusca (napisa): | i kak je rezultat u 4.15. b? meni je 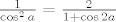
|
Ako te ta jednakost muči, to slijedi iz trigonometrijskih identiteta, ne iz limesa 
Tu je zapravo formula za polovični kut, koja kaže:
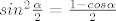

Ovo su inače jako korisne formule kod računanja integrala, pa ih je korisno imat negdje u glavi  |
zahvaljujem na savjetu ali to je jedno rjesenje u dva oblika, naveo sam oba cisto zato da mi netko ne kaze: 'ja sam dobio drukcije', a isto je 
@mornik: ne branim ti ja da rijesis cijeli zadatak, slobodno, samo mi ne moras otkriti sve  ipak je cilj da i ja malo razmisljam (za promjenu) ipak je cilj da i ja malo razmisljam (za promjenu) 
edit:
pretpostavio sam da ce hintovi biti dovoljni da shvatim. i jesu, ali imam jos dva sicusna pitanja:
1. zasto je 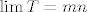 ? ?
2. sto da radim s tim kosinusima kad ih tak faktoriziram?? nisam nasao neku formulu ili nesto...
ovo je sve naravno pod pretpostavkom da si za 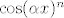 mislio mislio 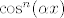 . . 
_________________
...to kaj ona ima kilu viska, ja ne marim...
Zadnja promjena: tmarusca; 17:06 sub, 9. 1. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
|
| [Vrh] |
|
|



















