| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
markotron
Forumaš(ica)
Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
MB
Forumaš(ica)
Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
markotron
Forumaš(ica)
Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol:
Lokacija: Umag
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)
Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)
Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
markotron
Forumaš(ica)
Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol:
Lokacija: Umag
|
|
| [Vrh] |
|
markotron
Forumaš(ica)
Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol:
Lokacija: Umag
|
|
| [Vrh] |
|
Gino
Forumaš(ica)
Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)
Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol:
|
|
| [Vrh] |
|
kyra29
Forumaš(ica)
Pridružen/a: 16. 02. 2009. (17:23:47)
Postovi: (3F)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)
Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol:
Lokacija: Hilbertov hotel
|
 Postano: 16:48 sri, 6. 1. 2010 Naslov: |
    |
|
|
ev ovak, neću pisat sve kak sam rješavo jer ne znam latex, pa bi bilo malo nakaradno, al ću probat objasnit šta sam radio
prvo sam f-ju rastavio na x*x, u slučaju kad je i x i y veće od nule, ili kad su oba manja od nule, onda -x*y i y*(-x) (što je zapravo jedno te isto) kad je x manji od nule, a y veći od nule, i kad je y manji od nule, a x veće od nule. i nula kad je x = y = 0.
dalje sad nemam vremena pisat, krećem za metropolu, al mislim da je ovo početak kaki bi trebo bit
ev ovak, neću pisat sve kak sam rješavo jer ne znam latex, pa bi bilo malo nakaradno, al ću probat objasnit šta sam radio
prvo sam f-ju rastavio na x*x, u slučaju kad je i x i y veće od nule, ili kad su oba manja od nule, onda -x*y i y*(-x) (što je zapravo jedno te isto) kad je x manji od nule, a y veći od nule, i kad je y manji od nule, a x veće od nule. i nula kad je x = y = 0.
dalje sad nemam vremena pisat, krećem za metropolu, al mislim da je ovo početak kaki bi trebo bit
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Lafiel
Forumaš(ica)
Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol:
|
| Postano: 18:33 sub, 9. 1. 2010 Naslov: |
|
|
|
Kaj nitko još nije počeo radit ili svi sve znaju? :oops:
[quote="Milojko"]i nula kad je x = y = 0.[/quote]
Ne mora nužno biti x=y=0, dovoljno je da je samo jedan od njih 0. :)
Pa evo nekoliko mojih pitanja:
[b]1. zadatak[/b]
[latex]f(x,y) = |(xy)|[/latex]
Treba izračunati parcijalne derivacije (gdje postoje), sve točke u kojima je funkcija diferencijabilna i diferencijal u nekoj točki.
Podijelila sam domenu na skupove
A = {(x,y) | x>0 i y<0 ili x<0 i y>0} i
B= {(x,y) | x<0 i y<0 ili x>0 i y>0}
i napisala kako je funkcija zadana na njima i u onom trećem slučaju.
E sad, pod uvjetom da nisam neš zeznula, dobijem da nema parcijalnih derivacija u točkama (0,y) i (x,0), osim u točki (0,0). Kaj bih ja sad trebala s tom točkom (0,0), moram provjeravati neprekidnost u njoj?
[b]2. zadatak[/b]
Ima netko ideju? Krenuh naime tražiti jednadžbu tangencijalne ravnine, ali nisam daleko dospjela. :?
[b]3. zadatak b)[/b]
Postiže li [latex]f(x,y) = x^2 -2y + \frac{9}{2}y^2[/latex] najveću i najmanju vrijednost na elipsi [latex]x^2 + 4y^2 = 25[/latex]
Prema teoremu o uvjetnim ekstremima dobijem [latex]\lambda = 1[/latex] pa mi je iz toga y=2 i x=+-3. Ali kad uvrstim točke (-3,2) i (3,2) u početnu funkciju, dobijem isti broj pa mi nije baš jasno kaj bih trebala raditi tj. što mi to znači. :?
Kaj nitko još nije počeo radit ili svi sve znaju? 
| Milojko (napisa): | | i nula kad je x = y = 0. |
Ne mora nužno biti x=y=0, dovoljno je da je samo jedan od njih 0.
Pa evo nekoliko mojih pitanja:
1. zadatak
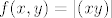
Treba izračunati parcijalne derivacije (gdje postoje), sve točke u kojima je funkcija diferencijabilna i diferencijal u nekoj točki.
Podijelila sam domenu na skupove
A = {(x,y) | x>0 i y<0 ili x<0 i y>0} i
B= {(x,y) | x<0 i y<0 ili x>0 i y>0}
i napisala kako je funkcija zadana na njima i u onom trećem slučaju.
E sad, pod uvjetom da nisam neš zeznula, dobijem da nema parcijalnih derivacija u točkama (0,y) i (x,0), osim u točki (0,0). Kaj bih ja sad trebala s tom točkom (0,0), moram provjeravati neprekidnost u njoj?
2. zadatak
Ima netko ideju? Krenuh naime tražiti jednadžbu tangencijalne ravnine, ali nisam daleko dospjela. 
3. zadatak b)
Postiže li 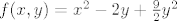 najveću i najmanju vrijednost na elipsi 
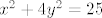
Prema teoremu o uvjetnim ekstremima dobijem 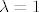 pa mi je iz toga y=2 i x=+-3. Ali kad uvrstim točke (-3,2) i (3,2) u početnu funkciju, dobijem isti broj pa mi nije baš jasno kaj bih trebala raditi tj. što mi to znači.
_________________
Weit von hier fällt Gold von den Sternen
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)
Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol:
Lokacija: Hilbertov hotel
|
| Postano: 20:30 sub, 9. 1. 2010 Naslov: |
|
|
|
[quote="Lafiel"]Kaj nitko još nije počeo radit ili svi sve znaju? :oops: [/quote]
reko bih ovo prvo
[quote="Lafel"]
E sad, pod uvjetom da nisam neš zeznula, dobijem da nema parcijalnih derivacija u točkama (0,y) i (x,0), osim u točki (0,0). Kaj bih ja sad trebala s tom točkom (0,0), moram provjeravati neprekidnost u njoj?
[/quote]
provjeri limes parcijalnih derivacija u okolini nule. to je onda potencijalni diferencijal jer bi to čudo od parc. der. moralo bit neprekidno dab f-ja bila dfb.
[quote="Lafel"]
[b]2. zadatak[/b]
Ima netko ideju? Krenuh naime tražiti jednadžbu tangencijalne ravnine, ali nisam daleko dospjela. :?
[/quote]
opći oblik tgc. ravnine u točki (x0,y0,z0), uvrštavaš u nju točke (x,0,0), (y,0,0), (z,0,0) da nađeš presjeke sa koordinatnim osima. negdje se u tome pojavi x0^2/3+y0^2/3+z0^2/3 (il eventualno sve pomnoženo sa minus jedan, ili tako nešto), a pošto je taj (x0,y0,z0) sa plohe, ta suma je jednaka a^2/3. prek toga izraziš x, y, z, i dobiš nešt tipa da je sve kad se kvadrira jednako a, ili tako neka konstanta.
Nisam riješio zad, vidio kod frenda rješenje, ovo je kolko se sjećam, sad ću oprobat.
[quote="Lafel"]
[b]3. zadatak b)[/b]
Postiže li [latex]f(x,y) = x^2 -2y + \frac{9}{2}y^2[/latex] najveću i najmanju vrijednost na elipsi [latex]x^2 + 4y^2 = 25[/latex]
Prema teoremu o uvjetnim ekstremima dobijem [latex]\lambda = 1[/latex] pa mi je iz toga y=2 i x=+-3. Ali kad uvrstim točke (-3,2) i (3,2) u početnu funkciju, dobijem isti broj pa mi nije baš jasno kaj bih trebala raditi tj. što mi to znači. :?[/quote]
e to i mene zanima. vjerojatno bi trebalo gledat kak se funkcija ponaša u okolini tih točaka, neke vražje limese računati, al, neam pojma zasad
| Lafiel (napisa): | | Kaj nitko još nije počeo radit ili svi sve znaju? |
reko bih ovo prvo
| Lafel (napisa): |
E sad, pod uvjetom da nisam neš zeznula, dobijem da nema parcijalnih derivacija u točkama (0,y) i (x,0), osim u točki (0,0). Kaj bih ja sad trebala s tom točkom (0,0), moram provjeravati neprekidnost u njoj?
|
provjeri limes parcijalnih derivacija u okolini nule. to je onda potencijalni diferencijal jer bi to čudo od parc. der. moralo bit neprekidno dab f-ja bila dfb.
| Lafel (napisa): |
2. zadatak
Ima netko ideju? Krenuh naime tražiti jednadžbu tangencijalne ravnine, ali nisam daleko dospjela.
|
opći oblik tgc. ravnine u točki (x0,y0,z0), uvrštavaš u nju točke (x,0,0), (y,0,0), (z,0,0) da nađeš presjeke sa koordinatnim osima. negdje se u tome pojavi x0^2/3+y0^2/3+z0^2/3 (il eventualno sve pomnoženo sa minus jedan, ili tako nešto), a pošto je taj (x0,y0,z0) sa plohe, ta suma je jednaka a^2/3. prek toga izraziš x, y, z, i dobiš nešt tipa da je sve kad se kvadrira jednako a, ili tako neka konstanta.
Nisam riješio zad, vidio kod frenda rješenje, ovo je kolko se sjećam, sad ću oprobat.
| Lafel (napisa): |
3. zadatak b)
Postiže li 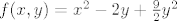najveću i najmanju vrijednost na elipsi
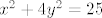
Prema teoremu o uvjetnim ekstremima dobijem 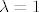pa mi je iz toga y=2 i x=+-3. Ali kad uvrstim točke (-3,2) i (3,2) u početnu funkciju, dobijem isti broj pa mi nije baš jasno kaj bih trebala raditi tj. što mi to znači. |
e to i mene zanima. vjerojatno bi trebalo gledat kak se funkcija ponaša u okolini tih točaka, neke vražje limese računati, al, neam pojma zasad
_________________ Sedam je prost broj
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Lafiel
Forumaš(ica)
Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol:
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)
Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
markotron
Forumaš(ica)
Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol:
Lokacija: Umag
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)
Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol:
|
| Postano: 15:59 ned, 10. 1. 2010 Naslov: |
|
|
|
[quote="Mr.Doe"]Ovdje je poanta da skuzis da je dana elipsa omeden i zatvoren skup, pa stoga kompaktan. A na MA2 se dokazivao jedan teorem koji govori da neprekidna funkcija na kompaktnom skupu poprima min i max. Ako bas zelis (lagano) naci te tocke i vrijednosti mozes iz uvjeta (tj. jed. elipse) izraziti x( koji ce ovisiti o y) ili y(koji ce ovisiti o x), te ga upiknuti u funkciju, i onda traziti ekstreme funkcije jedne varijable( naravno biti ce neki uvjeti na tu varijablu).[/quote]
Najbolje od svega, prvo sam krenula tako, pokazala da je to kompaktan skup i napisala da onda slijedi da funkcija na njemu poprima minimum i maksimum, ali sam onda, kad sam dobila one dvije točke koje mi daju istu vrijednost kad ih uvrstim u funkciju, mislila da sam nešto krivo napravila. :oops:
| Mr.Doe (napisa): | | Ovdje je poanta da skuzis da je dana elipsa omeden i zatvoren skup, pa stoga kompaktan. A na MA2 se dokazivao jedan teorem koji govori da neprekidna funkcija na kompaktnom skupu poprima min i max. Ako bas zelis (lagano) naci te tocke i vrijednosti mozes iz uvjeta (tj. jed. elipse) izraziti x( koji ce ovisiti o y) ili y(koji ce ovisiti o x), te ga upiknuti u funkciju, i onda traziti ekstreme funkcije jedne varijable( naravno biti ce neki uvjeti na tu varijablu). |
Najbolje od svega, prvo sam krenula tako, pokazala da je to kompaktan skup i napisala da onda slijedi da funkcija na njemu poprima minimum i maksimum, ali sam onda, kad sam dobila one dvije točke koje mi daju istu vrijednost kad ih uvrstim u funkciju, mislila da sam nešto krivo napravila.
_________________
Weit von hier fällt Gold von den Sternen
|
|
| [Vrh] |
|
markotron
Forumaš(ica)
Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol:
Lokacija: Umag
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)
Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol:
|
|
| [Vrh] |
|
storm_1
Forumaš(ica)
Pridružen/a: 11. 01. 2010. (15:38:41)
Postovi: (2)16
|
|
| [Vrh] |
|
|
nije to pejzaž da se opisuje 
Thx.
Thx, to je ta ključna informacija koja mi je trebala. 
