| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 20:49 uto, 19. 1. 2010 Naslov: Postano: 20:49 uto, 19. 1. 2010 Naslov: |
    |
|
|
Dobro je eve objasnila, nema baš nekog principa po kojem se to vrši - ideš unazad i gledaš što ti treba. Dakle, probaj rješavati (zapravo, ne rješavati koliko malo razmišljati kako bi došao/došla do rješenja) zadatak/primjer/teorem bez toga da na početku uzimaš takve "čudne" vrijednosti. Nakon nekog vremena ćeš vidjeti otprilike kakva svojstva želiš da ti vrijede i onda ćeš probati nekako namjestiti deltu (ili što već) da ti zadovoljava upravo ta svojstva. Nadam se da ima smisla otprilike što želim reći :).
Tako bi, na primjer, u teoremu 2.4., 3. dio, rezoniranje išlo nekako ovako (naravno, ne radi se o matematički preciznom tekstu, više pokušaju zdravorazumskog objašnjenja :)): Mi želimo da za svaki [latex]\epsilon>0[/latex] i "dovoljno veliki" [latex]n\in\mathbb{N}[/latex] ovisan o epsilonu vrijedi [latex]\displaystyle |\frac{1}{b_n}-\frac{1}{b}|<\epsilon[/latex]. To je očito ekvivalentno s [latex]\displaystyle \frac{|b-b_n|}{|b_n\cdot b|}<\epsilon[/latex]. Sad, primjećujemo dvije stvari:
Prvo, moramo nekako osigurati da [latex]b_n\neq 0[/latex] za sve dovoljno velike [latex]n[/latex] (čisto zato da nazivnik postoji). To je intuitivno dosta jasno, budući da [latex]b_n\to b\neq 0[/latex], pa "znamo" da će nakon konačno mnogo [latex]n[/latex] svi [latex]b_n[/latex] biti "jako blizu" [latex]b[/latex], a kako [latex]b\neq 0[/latex], onda će biti dovoljno udaljeni od nule. Za preciznu izvedbu te ideje služi prvi dio dokaza u skripti.
Drugo (i to je ono što si ti zapravo pitao/pitala), mi znamo da je nazivnik "otprilike jednak" [latex]|b\cdot b|[/latex] (jer [latex]b_n\to b[/latex]). Stoga hoćemo ovaj [latex]b-b_n[/latex] nekako natjerati da bude takav da se pokrati s tim [latex]b^2[/latex] u nazivniku. Naravno, sad dolazi ovaj dio u skripti koji mi je nejasan (tj. vjerojatno se radi u tipfeleru) :). Naime, iz gore izloženog je nekako dosta jasno da bismo htjeli uzeti nešto povezano s [latex]|b|^2\epsilon[/latex] za ograničenje razlike između [latex]b_n[/latex] i [latex]b[/latex]. Kako se pokaže (recimo, u trenutku kad pokazujemo da je [latex]|b_n|>0[/latex] za dovoljno velike [latex]n[/latex]) da je [latex]\displaystyle |b_n|>\frac{b}{2}[/latex]), korisno nam je uzeti [latex]\displaystyle |b_n-b|<\frac{|b|^2\epsilon}{2}[/latex], što svakako možemo reći budući da je [latex]|b|^2\epsilon>0[/latex]. Zašto se u skripti nalazi [latex]\displaystyle \frac{2\epsilon}{|b|^2}[/latex], ne znam niti mi se čini da to onda dobro ispada u sljedećem redu :? (makar se i time, dakako, uz još malo razmišljanja dobiva točan rezultat).
U svakom slučaju, ja bih uzeo [latex]\frac{b^2\epsilon}{2}[/latex] (zapravo ne bih, jer sam glup, pa me Genaro ispravio par postova poslije :P) i time lako dobivamo (znamo da je [latex]\displaystyle |b_n|>\frac{b}{2}[/latex]) da je [latex]\displaystyle \frac{|b-b_n|}{|b_n\cdot b|}<\frac{b^2\epsilon}{b^2}=\epsilon[/latex] i to je to.
Evo, nadam se da sam objasnio ideju u ovom primjeru, a radi li se o tipfeleru ili ne, ne znam, samo znam da mi ovo u skripti na prvi pogled baš i nema smisla, ali možda sam glup, događa se to dosta često :D.
Probat ću još objasniti i drugi primjer koji spominješ, makar ne vidim gdje se javlja [latex]\displaystyle\frac{2\epsilon}{5|c|}[/latex] iz tvog posta (another typo?) :?. Uglavnom, krećemo "od kraja": želimo pokazati da za svaki [latex]\epsilon>0[/latex] i za svaki [latex]x[/latex] "dovoljno blizu" [latex]c\neq 0[/latex] vrijedi [latex]\displaystyle |\frac{1}{x}-\frac{1}{c}|<\epsilon[/latex]. Očito, to je ekvivalentno s [latex]\displaystyle \frac{|x-c|}{|x||c|}<\epsilon[/latex]. Sad opet imamo ista dva pitanja kao u prethodnom primjeru:
Prvo, želimo osigurati [latex]x\neq 0[/latex] za [latex]x[/latex] "dovoljno blizu" [latex]c[/latex]. Najpopularniji način za osiguravanje toga je dakako[latex]\displaystyle |x-c|<\frac{|c|}{2}[/latex], iz čega se izvodi [latex]\displaystyle |x|>\frac{|c|}{2}>0[/latex]. To je upravo ono što se pojavljuje u prvom dijelu.
Drugo pitanje je "važnije" - treba natjerati [latex]x[/latex] da bude takav da [latex]|x-c|<\epsilon|x||c|[/latex]. Tu mi se zapravo čini da bi prošla i ista ideja kao u teoremu kojeg smo diskutirali, ali neću zbunjivati, nije (puno :)) jednostavnije, a i možda je ovo praktičnije jer smo pola posla već obavili u prvom pitanju.
U svakom slučaju, iskoristit ćemo prvo prvi dio i dobiti da nam iz njega vrijedi [latex]\displaystyle \frac{\epsilon |c|^2}{2}<\epsilon |x||c|[/latex]. Desna strana nam odgovara, sad samo, dakle, valjda nagovoriti [latex]x[/latex] da bude takav da vrijedi još i [latex]\displaystyle |x-c|<\frac{\epsilon |c|^2}{2}[/latex], a to je upravo ovaj drugi dio u definiciji [latex]\delta[/latex]. Uzimamo, naravno, minimum jer želimo da nam oba uvjeta vrijede - ako je razlika manja od manjeg od dva broja, manja je od oba broja.
Naravno, kao što rekoh, ovo je sve objašnjeno dosta neprecizno, u skripti je to sve matematički rigoroznije, ali ja sam probao sada dati ideju.
EDIT: Ispravljeno. Hvala Genaro :).
Dobro je eve objasnila, nema baš nekog principa po kojem se to vrši - ideš unazad i gledaš što ti treba. Dakle, probaj rješavati (zapravo, ne rješavati koliko malo razmišljati kako bi došao/došla do rješenja) zadatak/primjer/teorem bez toga da na početku uzimaš takve "čudne" vrijednosti. Nakon nekog vremena ćeš vidjeti otprilike kakva svojstva želiš da ti vrijede i onda ćeš probati nekako namjestiti deltu (ili što već) da ti zadovoljava upravo ta svojstva. Nadam se da ima smisla otprilike što želim reći  . .
Tako bi, na primjer, u teoremu 2.4., 3. dio, rezoniranje išlo nekako ovako (naravno, ne radi se o matematički preciznom tekstu, više pokušaju zdravorazumskog objašnjenja  ): Mi želimo da za svaki ): Mi želimo da za svaki 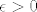 i "dovoljno veliki" i "dovoljno veliki" 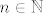 ovisan o epsilonu vrijedi ovisan o epsilonu vrijedi 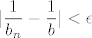 . To je očito ekvivalentno s . To je očito ekvivalentno s 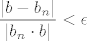 . Sad, primjećujemo dvije stvari: . Sad, primjećujemo dvije stvari:
Prvo, moramo nekako osigurati da 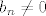 za sve dovoljno velike za sve dovoljno velike  (čisto zato da nazivnik postoji). To je intuitivno dosta jasno, budući da (čisto zato da nazivnik postoji). To je intuitivno dosta jasno, budući da 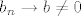 , pa "znamo" da će nakon konačno mnogo , pa "znamo" da će nakon konačno mnogo  svi svi 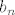 biti "jako blizu" biti "jako blizu" 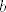 , a kako , a kako 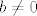 , onda će biti dovoljno udaljeni od nule. Za preciznu izvedbu te ideje služi prvi dio dokaza u skripti. , onda će biti dovoljno udaljeni od nule. Za preciznu izvedbu te ideje služi prvi dio dokaza u skripti.
Drugo (i to je ono što si ti zapravo pitao/pitala), mi znamo da je nazivnik "otprilike jednak" 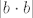 (jer (jer  ). Stoga hoćemo ovaj ). Stoga hoćemo ovaj  nekako natjerati da bude takav da se pokrati s tim nekako natjerati da bude takav da se pokrati s tim 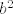 u nazivniku. Naravno, sad dolazi ovaj dio u skripti koji mi je nejasan (tj. vjerojatno se radi u tipfeleru) u nazivniku. Naravno, sad dolazi ovaj dio u skripti koji mi je nejasan (tj. vjerojatno se radi u tipfeleru)  . Naime, iz gore izloženog je nekako dosta jasno da bismo htjeli uzeti nešto povezano s . Naime, iz gore izloženog je nekako dosta jasno da bismo htjeli uzeti nešto povezano s 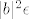 za ograničenje razlike između za ograničenje razlike između 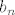 i i 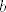 . Kako se pokaže (recimo, u trenutku kad pokazujemo da je . Kako se pokaže (recimo, u trenutku kad pokazujemo da je 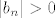 za dovoljno velike za dovoljno velike  ) da je ) da je 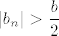 ), korisno nam je uzeti ), korisno nam je uzeti 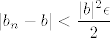 , što svakako možemo reći budući da je , što svakako možemo reći budući da je 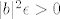 . Zašto se u skripti nalazi . Zašto se u skripti nalazi 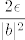 , ne znam niti mi se čini da to onda dobro ispada u sljedećem redu , ne znam niti mi se čini da to onda dobro ispada u sljedećem redu  (makar se i time, dakako, uz još malo razmišljanja dobiva točan rezultat). (makar se i time, dakako, uz još malo razmišljanja dobiva točan rezultat).
U svakom slučaju, ja bih uzeo 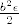 (zapravo ne bih, jer sam glup, pa me Genaro ispravio par postova poslije (zapravo ne bih, jer sam glup, pa me Genaro ispravio par postova poslije  ) i time lako dobivamo (znamo da je ) i time lako dobivamo (znamo da je 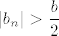 ) da je ) da je 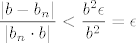 i to je to. i to je to.
Evo, nadam se da sam objasnio ideju u ovom primjeru, a radi li se o tipfeleru ili ne, ne znam, samo znam da mi ovo u skripti na prvi pogled baš i nema smisla, ali možda sam glup, događa se to dosta često  . .
Probat ću još objasniti i drugi primjer koji spominješ, makar ne vidim gdje se javlja 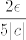 iz tvog posta (another typo?) iz tvog posta (another typo?)  . Uglavnom, krećemo "od kraja": želimo pokazati da za svaki . Uglavnom, krećemo "od kraja": želimo pokazati da za svaki 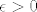 i za svaki i za svaki  "dovoljno blizu" "dovoljno blizu" 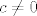 vrijedi vrijedi 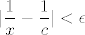 . Očito, to je ekvivalentno s . Očito, to je ekvivalentno s 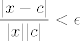 . Sad opet imamo ista dva pitanja kao u prethodnom primjeru: . Sad opet imamo ista dva pitanja kao u prethodnom primjeru:
Prvo, želimo osigurati 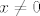 za za  "dovoljno blizu" "dovoljno blizu"  . Najpopularniji način za osiguravanje toga je dakako . Najpopularniji način za osiguravanje toga je dakako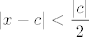 , iz čega se izvodi , iz čega se izvodi 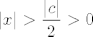 . To je upravo ono što se pojavljuje u prvom dijelu. . To je upravo ono što se pojavljuje u prvom dijelu.
Drugo pitanje je "važnije" - treba natjerati  da bude takav da da bude takav da 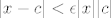 . Tu mi se zapravo čini da bi prošla i ista ideja kao u teoremu kojeg smo diskutirali, ali neću zbunjivati, nije (puno . Tu mi se zapravo čini da bi prošla i ista ideja kao u teoremu kojeg smo diskutirali, ali neću zbunjivati, nije (puno  ) jednostavnije, a i možda je ovo praktičnije jer smo pola posla već obavili u prvom pitanju. ) jednostavnije, a i možda je ovo praktičnije jer smo pola posla već obavili u prvom pitanju.
U svakom slučaju, iskoristit ćemo prvo prvi dio i dobiti da nam iz njega vrijedi 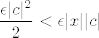 . Desna strana nam odgovara, sad samo, dakle, valjda nagovoriti . Desna strana nam odgovara, sad samo, dakle, valjda nagovoriti  da bude takav da vrijedi još i da bude takav da vrijedi još i 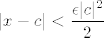 , a to je upravo ovaj drugi dio u definiciji , a to je upravo ovaj drugi dio u definiciji  . Uzimamo, naravno, minimum jer želimo da nam oba uvjeta vrijede - ako je razlika manja od manjeg od dva broja, manja je od oba broja. . Uzimamo, naravno, minimum jer želimo da nam oba uvjeta vrijede - ako je razlika manja od manjeg od dva broja, manja je od oba broja.
Naravno, kao što rekoh, ovo je sve objašnjeno dosta neprecizno, u skripti je to sve matematički rigoroznije, ali ja sam probao sada dati ideju.
EDIT: Ispravljeno. Hvala Genaro  . .
Zadnja promjena: mornik; 7:39 sri, 20. 1. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 21:39 uto, 19. 1. 2010 Naslov: Postano: 21:39 uto, 19. 1. 2010 Naslov: |
    |
|
|
Pa, i meni se čini da je tipfeler, ali zar ne bi trebalo ići ovako:
Znamo da je [latex]\displaystyle \vert b_{n} \vert \leqslant \frac{\vert b \vert}{2} \Rightarrow \frac{1}{\vert b_{n} \vert} \geqslant \frac{2}{\vert b \vert}[/latex]
Sada uzmemo da je [latex] \displaystyle \vert b_{n}-b \vert < \frac{\epsilon {\vert b \vert}^{2}}{2}{[/latex].
I na kraju imamo [latex]\displaystyle \vert \frac{1}{b_{n}}-\frac{1}{b} \vert = \frac{\vert b - b_{n} \vert }{\vert b_{n}\vert \vert b \vert } < \frac{\epsilon {\vert b \vert}^{2}}{2} \cdot \frac{2}{ {\vert b \vert}^{2}} = \epsilon{[/latex]
Čini mi se da stvarno je tipfeler, a možda sam i ja samo glup :D
No, što sam želio pitati je ako je moguće malo pojašnjenje leme kojom dokazujemo B.W: teorem za nizove, tj:
Svaki niz [latex](a_{n})\ u\ \mathbb{R}[/latex] ima monoton podniz.
Znam da je vjerojatno jednostavno, ali ne idu mi u glavu nikako ti podnizovi.
Pa, i meni se čini da je tipfeler, ali zar ne bi trebalo ići ovako:
Znamo da je 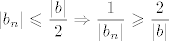
Sada uzmemo da je 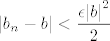 . .
I na kraju imamo 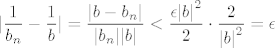
Čini mi se da stvarno je tipfeler, a možda sam i ja samo glup 
No, što sam želio pitati je ako je moguće malo pojašnjenje leme kojom dokazujemo B.W: teorem za nizove, tj:
Svaki niz 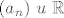 ima monoton podniz. ima monoton podniz.
Znam da je vjerojatno jednostavno, ali ne idu mi u glavu nikako ti podnizovi.
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 22:07 uto, 19. 1. 2010 Naslov: Postano: 22:07 uto, 19. 1. 2010 Naslov: |
    |
|
|
Ideja u dokazivanju BW:
Postoje tri moguca slucaja:
1. Da je niz takav da za bilo koji n_0 skup koji sadrzi sve clanove clanove niza a_n t.d n >= n_0 nema najveci element.
2. Da je niz takav da skup koji sadrzi sve clanove niza ima najveci element, ali da postoji takav N, da za svaki n_0 >= N vrijedi prva tvrdnja.
3. Jedini preostali slucaj je da za svaki n_0 skup koji sadrzi sve clanove niza a_n t.d n >= n_0 skup ima najveci element.
Primjer za prvi slucaj bi bio recimo niz a_n = 2 - 1/n (dakle, kad uzmes skup elemenata on nikad nema najveci element jer koji god da uzmes onaj element iza njega je veci)
Primjer za drugi bi bio npr a_1 = ... = a_5 = 0, a_6 = 3, a_n = 2 - 1/n, za n >= 7 (dakle u pocetku se mogu dogoditi neki elementi koji su veci od svih clanova niza, ali kad njih prodes, onda ti se ostatak ponasa kao u prvom slucaju).
Treci primjer bi bio npr 1/n (dakle u svakom koraku znas koji je element najveci u cijelom preostalom dijelu niza)
U prvom slucaju sad ides graditi rastuci podniz, kako nema nikad najveceg elementa, ne moras se brinuti da ces se negdje "zabiti" slucajno, pa samo uzmes prvi element niza. Kako nema najveceg, onda on nije najveci, pa postoji neki poslije njega koji je veci - uzmes da ti on bude drugi element podniza. Opet on ne smije biti najveci, pa uzmes slijedeci i tako dalje...
U drugom slucaju ovih "problematicnih" elemenata moze biti samo konacno mnogo, pa ih jednostavno izignoriras i krenes od tamo gdje je niz lijep. Sad je to potpuno isto kao u prvom slucaju.
U trecem slucaju uzmes za prvi clan niza najveci element. U preostalom dijelu niza sad mora opet postojati neki najveci element i on je sigurno manji ili jednak ovome kojeg vec imas (jer je prije taj bio najveci), pa tog uzmes za drugi element podniza. Sad opet mora postojati neki koji je u dijelu niza nakon njega najveci, i tako dalje...
Ideja u dokazivanju BW:
Postoje tri moguca slucaja:
1. Da je niz takav da za bilo koji n_0 skup koji sadrzi sve clanove clanove niza a_n t.d n >= n_0 nema najveci element.
2. Da je niz takav da skup koji sadrzi sve clanove niza ima najveci element, ali da postoji takav N, da za svaki n_0 >= N vrijedi prva tvrdnja.
3. Jedini preostali slucaj je da za svaki n_0 skup koji sadrzi sve clanove niza a_n t.d n >= n_0 skup ima najveci element.
Primjer za prvi slucaj bi bio recimo niz a_n = 2 - 1/n (dakle, kad uzmes skup elemenata on nikad nema najveci element jer koji god da uzmes onaj element iza njega je veci)
Primjer za drugi bi bio npr a_1 = ... = a_5 = 0, a_6 = 3, a_n = 2 - 1/n, za n >= 7 (dakle u pocetku se mogu dogoditi neki elementi koji su veci od svih clanova niza, ali kad njih prodes, onda ti se ostatak ponasa kao u prvom slucaju).
Treci primjer bi bio npr 1/n (dakle u svakom koraku znas koji je element najveci u cijelom preostalom dijelu niza)
U prvom slucaju sad ides graditi rastuci podniz, kako nema nikad najveceg elementa, ne moras se brinuti da ces se negdje "zabiti" slucajno, pa samo uzmes prvi element niza. Kako nema najveceg, onda on nije najveci, pa postoji neki poslije njega koji je veci - uzmes da ti on bude drugi element podniza. Opet on ne smije biti najveci, pa uzmes slijedeci i tako dalje...
U drugom slucaju ovih "problematicnih" elemenata moze biti samo konacno mnogo, pa ih jednostavno izignoriras i krenes od tamo gdje je niz lijep. Sad je to potpuno isto kao u prvom slucaju.
U trecem slucaju uzmes za prvi clan niza najveci element. U preostalom dijelu niza sad mora opet postojati neki najveci element i on je sigurno manji ili jednak ovome kojeg vec imas (jer je prije taj bio najveci), pa tog uzmes za drugi element podniza. Sad opet mora postojati neki koji je u dijelu niza nakon njega najveci, i tako dalje...
_________________
Bri
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 7:33 sri, 20. 1. 2010 Naslov: Postano: 7:33 sri, 20. 1. 2010 Naslov: |
    |
|
|
@Genaro: Ma da, u pravu si. Mislim, poanta je uzeti [latex]b^2\epsilon[/latex], a onda nam je vjerojatno najlakše još to podijeliti s [latex]2[/latex] upravo iz razloga koji si rekao :). Zanio sam se malo s zdravorazumskim objašnjavanjem, tako da matematički ovo moje baš i nije stajalo :oops:. Sad ću ispraviti to.
@Andra:
Neka je [latex]x<y[/latex]. Želiš pokazati da je [latex]x^3<y^3[/latex]. To je ekvivalentno s [latex](y-x)(y^2+xy+x^2)>0[/latex]. Kako je [latex]y-x>0[/latex], moraš pokazati da je [latex]y^2+xy+x^2>0[/latex]. To je poznata tvrdnja, ali ćemo ju svejedno dokazati. Idemo sad putem koji mi se trenutno čini najjednostavniji :). Ako je [latex]y=0[/latex], onda treba pokazati [latex]x^2>0[/latex], što stoji, budući da [latex]x\neq y=0[/latex]. Inače, podijelimo sve s [latex]y^2[/latex] i dobivamo [latex]\displaystyle 1+\frac{x}{y}+(\frac{x}{y})^2>0[/latex]. Ako uvrstimo [latex]\displaystyle t=\frac{x}{y}[/latex], dobivamo da želimo pokazati da za svaki [latex]t[/latex] vrijedi [latex]1+t+t^2>0[/latex], a to lako pokažeš (rješavanjem kvadratne jednadžbe ili čega već).
Za [latex]x^5[/latex] imamo nešto jednostavniji način. Zapravo, doslovno, ali doslovno, isti način radi i za [latex]x^3[/latex], tako da možeš slobodno zanemariti sve ovo napisano gore i izvesti ovaj isti dokaz (samo mijenjaj [latex]5[/latex] u [latex]3[/latex]) :lol:. Dakle, [latex]x<y[/latex] i želimo pokazati da je [latex]x^5<y^5[/latex]. Razlikovat ćemo dva slučaja:
Prvo, neka je [latex]y>0[/latex]. Tada je gornja nejednakost ekvivalentna s [latex]\displaystyle (\frac{x}{y})^5<1[/latex], što svakako stoji budući da je [latex]\displaystyle \frac{x}{y}<1[/latex] (to je u ovom slučaju ekvivalentno s [latex]x<y[/latex]).
Drugo, neka je [latex]y<0[/latex] (za [latex]y=0[/latex] trivijalno vidimo da tvrdnja stoji jer onda vrijedi [latex]x<0[/latex], pa i [latex]x^5<0=y^5[/latex]). Tada je gornja nejednakost ekvivalentna s [latex]\displaystyle (\frac{x}{y})^5>1[/latex]. U ovom slučaju, to je točno budući da je [latex]\displaystyle \frac{x}{y}>1[/latex] (kad pomnožimo s [latex]y[/latex] i promijenimo znak nejednakosti, to je opet ekvivalentno s [latex]x<y[/latex]).
Evo, kažem, ovaj način koji sam izveo za [latex]x^5[/latex] djeluje i za treće potencije i puno je lakši :).
@Genaro: Ma da, u pravu si. Mislim, poanta je uzeti 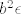 , a onda nam je vjerojatno najlakše još to podijeliti s , a onda nam je vjerojatno najlakše još to podijeliti s  upravo iz razloga koji si rekao upravo iz razloga koji si rekao  . Zanio sam se malo s zdravorazumskim objašnjavanjem, tako da matematički ovo moje baš i nije stajalo . Zanio sam se malo s zdravorazumskim objašnjavanjem, tako da matematički ovo moje baš i nije stajalo  . Sad ću ispraviti to. . Sad ću ispraviti to.
@Andra:
Neka je 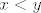 . Želiš pokazati da je . Želiš pokazati da je 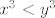 . To je ekvivalentno s . To je ekvivalentno s 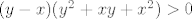 . Kako je . Kako je 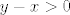 , moraš pokazati da je , moraš pokazati da je 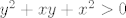 . To je poznata tvrdnja, ali ćemo ju svejedno dokazati. Idemo sad putem koji mi se trenutno čini najjednostavniji . To je poznata tvrdnja, ali ćemo ju svejedno dokazati. Idemo sad putem koji mi se trenutno čini najjednostavniji  . Ako je . Ako je 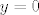 , onda treba pokazati , onda treba pokazati 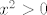 , što stoji, budući da , što stoji, budući da 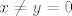 . Inače, podijelimo sve s . Inače, podijelimo sve s 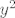 i dobivamo i dobivamo 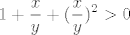 . Ako uvrstimo . Ako uvrstimo 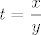 , dobivamo da želimo pokazati da za svaki , dobivamo da želimo pokazati da za svaki  vrijedi vrijedi 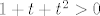 , a to lako pokažeš (rješavanjem kvadratne jednadžbe ili čega već). , a to lako pokažeš (rješavanjem kvadratne jednadžbe ili čega već).
Za 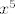 imamo nešto jednostavniji način. Zapravo, doslovno, ali doslovno, isti način radi i za imamo nešto jednostavniji način. Zapravo, doslovno, ali doslovno, isti način radi i za 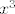 , tako da možeš slobodno zanemariti sve ovo napisano gore i izvesti ovaj isti dokaz (samo mijenjaj , tako da možeš slobodno zanemariti sve ovo napisano gore i izvesti ovaj isti dokaz (samo mijenjaj  u u 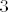 ) )  . Dakle, . Dakle, 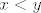 i želimo pokazati da je i želimo pokazati da je 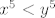 . Razlikovat ćemo dva slučaja: . Razlikovat ćemo dva slučaja:
Prvo, neka je 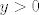 . Tada je gornja nejednakost ekvivalentna s . Tada je gornja nejednakost ekvivalentna s 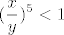 , što svakako stoji budući da je , što svakako stoji budući da je 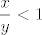 (to je u ovom slučaju ekvivalentno s (to je u ovom slučaju ekvivalentno s 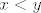 ). ).
Drugo, neka je 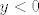 (za (za 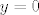 trivijalno vidimo da tvrdnja stoji jer onda vrijedi trivijalno vidimo da tvrdnja stoji jer onda vrijedi 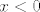 , pa i , pa i 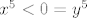 ). Tada je gornja nejednakost ekvivalentna s ). Tada je gornja nejednakost ekvivalentna s 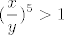 . U ovom slučaju, to je točno budući da je . U ovom slučaju, to je točno budući da je 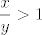 (kad pomnožimo s (kad pomnožimo s  i promijenimo znak nejednakosti, to je opet ekvivalentno s i promijenimo znak nejednakosti, to je opet ekvivalentno s 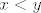 ). ).
Evo, kažem, ovaj način koji sam izveo za 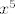 djeluje i za treće potencije i puno je lakši djeluje i za treće potencije i puno je lakši  . .
|
|
| [Vrh] |
|
zekoo
Forumaš(ica)


Pridružen/a: 31. 10. 2009. (22:58:36)
Postovi: (12)16
Spol: 
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
 Postano: 0:00 pet, 29. 1. 2010 Naslov: Postano: 0:00 pet, 29. 1. 2010 Naslov: |
    |
|
|
pa da...pita primjere,tipa neprekidnost f-je sinus,neprekidnost f-je 1/x, x^2,dokaz da je [latex]\lim_{x \to 0}\frac{sin(x)}{x}=1[/latex], i tako...
pa da...pita primjere,tipa neprekidnost f-je sinus,neprekidnost f-je 1/x, x^2,dokaz da je 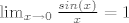 , i tako... , i tako...
_________________
You'll take my life but I'll take yours too
You'll fire your musket but I'll run you through
So when you're waiting for the next attack
You'd better stand there's no turning back
|
|
| [Vrh] |
|
|
















