| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
 Postano: 21:24 sri, 24. 2. 2010 Naslov: Postano: 21:24 sri, 24. 2. 2010 Naslov: |
    |
|
|
[quote="pajopatak"]Dali bi znao netko rješiti onaj zadatak što je asistent Berić dao za dz, onaj u kojem je zadana matrica B,i preslikavanje f:M2(F)--> M2(F). Dali je tu A neka proizvoljna kvadratna matrica ili?[/quote]
A je proizvoljna matrica reda 2, jer je to domena linearnog operatora(koji to stvarno jest zbog distributivnosti mnozenja). Kad napises matricu A u opcenitom obliku, pomnozi AB i BA te imas da za KerA vrijedi AB=BA i dobijes defekt 2, a prema teoremu o rangu i defektu je i rang 2, a baze dobijes cistim raspisom faktora.
| pajopatak (napisa): | | Dali bi znao netko rješiti onaj zadatak što je asistent Berić dao za dz, onaj u kojem je zadana matrica B,i preslikavanje f:M2(F)→ M2(F). Dali je tu A neka proizvoljna kvadratna matrica ili? |
A je proizvoljna matrica reda 2, jer je to domena linearnog operatora(koji to stvarno jest zbog distributivnosti mnozenja). Kad napises matricu A u opcenitom obliku, pomnozi AB i BA te imas da za KerA vrijedi AB=BA i dobijes defekt 2, a prema teoremu o rangu i defektu je i rang 2, a baze dobijes cistim raspisom faktora.
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 20:37 čet, 25. 2. 2010 Naslov: Postano: 20:37 čet, 25. 2. 2010 Naslov: |
    |
|
|
Gledas prvo sta je Ker(D). To je skup svih polinoma koji se slikaju u nulu, tj. nul-polinom. Znaci da izraz p(t+a)-p(t) mora bit nul-polinom.
Sad uzmes da je p proizvoljan polinom stupnja k<=n, tj stavimo [latex]p(t)=\sum_{i=0}^k{\alpha_it^i}[/latex]
Pogledamo sta je p(t+a)-p(t) i dobijemo da to izgleda ovako: [latex]2\alpha_kat^{k-1}+\dots[/latex] (bitan nam je samo ovaj vodeci clan) (*)
sad ocito da ovo nije nulpolinom cim je [latex]\alpha_k\neq0[/latex]
Tj, sad smo dobili da je za svaki polinom p stupnja 1 ili vise, [latex]Dp\neq0[/latex]
Ostao je jos samo slucaj kad je p=konst. Tada je ocito p(a+t)-p(t)=konst-konst=0, dakle svi konstantni polinomi slikaju se u nulu.
S ovim smo zapravo obavili vecinu posla, jer sad dalje zakljucujemo:
1) KerD cine samo konstantni polinomi, pa je baza za Ker neki jednoclan skup koji sadrzi polinom stupnja 0, npr {1}. Iz ovog takodjer imamo defekt(D)=1
2) iz tm. o rangu i defektu i cinjenice da je d(D)=1 zakljucujemo r(D)=n (jer je dimV=n+1)
3) gornji racun (*) je pokazao da operator D slika sve polinome iz Pn u skup [latex]P_{n-1}[/latex] (polinomi stupnja najvise n-1; to je slucaj kada k=n)
Sada znamo da je [latex]ImD\leq P_{n-1}[/latex], a imamo i [latex]r(D)=dim(P_{n-1})[/latex] pa mora biti [latex]ImD=P_{n-1}[/latex] (kad je potprostor jednake dimenzije kao i "nadprostor", tada su oni jednaki)
Ovime smo odredili i ImD, a za bazu od ImD uzmemo bilo koju bazu za P(n-1), npr {1,t,t^2,...,t^(n-1)}
Gledas prvo sta je Ker(D). To je skup svih polinoma koji se slikaju u nulu, tj. nul-polinom. Znaci da izraz p(t+a)-p(t) mora bit nul-polinom.
Sad uzmes da je p proizvoljan polinom stupnja k⇐n, tj stavimo 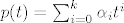
Pogledamo sta je p(t+a)-p(t) i dobijemo da to izgleda ovako: 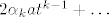 (bitan nam je samo ovaj vodeci clan) (*) (bitan nam je samo ovaj vodeci clan) (*)
sad ocito da ovo nije nulpolinom cim je 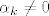
Tj, sad smo dobili da je za svaki polinom p stupnja 1 ili vise, 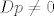
Ostao je jos samo slucaj kad je p=konst. Tada je ocito p(a+t)-p(t)=konst-konst=0, dakle svi konstantni polinomi slikaju se u nulu.
S ovim smo zapravo obavili vecinu posla, jer sad dalje zakljucujemo:
1) KerD cine samo konstantni polinomi, pa je baza za Ker neki jednoclan skup koji sadrzi polinom stupnja 0, npr {1}. Iz ovog takodjer imamo defekt(D)=1
2) iz tm. o rangu i defektu i cinjenice da je d(D)=1 zakljucujemo r(D)=n (jer je dimV=n+1)
3) gornji racun (*) je pokazao da operator D slika sve polinome iz Pn u skup 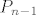 (polinomi stupnja najvise n-1; to je slucaj kada k=n) (polinomi stupnja najvise n-1; to je slucaj kada k=n)
Sada znamo da je 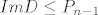 , a imamo i , a imamo i 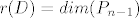 pa mora biti pa mora biti 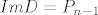 (kad je potprostor jednake dimenzije kao i "nadprostor", tada su oni jednaki) (kad je potprostor jednake dimenzije kao i "nadprostor", tada su oni jednaki)
Ovime smo odredili i ImD, a za bazu od ImD uzmemo bilo koju bazu za P(n-1), npr {1,t,t^2,...,t^(n-1)}
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
 Postano: 16:12 sub, 13. 3. 2010 Naslov: Postano: 16:12 sub, 13. 3. 2010 Naslov: |
    |
|
|
http://web.math.hr/nastava/la/kolokviji/08-09/la2/kol1a.pdf 2.
Načelno znam kako bih riješila zadatak , ali imam problema s bazama u kojim je A zadan i s ovom {A(1),A(t),A(t^2)}
...eto,ako je tko voljan pomoći,hvala :)
http://web.math.hr/nastava/la/kolokviji/08-09/la2/kol1a.pdf 2.
Načelno znam kako bih riješila zadatak , ali imam problema s bazama u kojim je A zadan i s ovom {A(1),A(t),A(t^2)}
...eto,ako je tko voljan pomoći,hvala 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 16:47 sub, 13. 3. 2010 Naslov: Postano: 16:47 sub, 13. 3. 2010 Naslov: |
    |
|
|
[quote="NeonBlack"]http://web.math.hr/nastava/la/kolokviji/08-09/la2/kol1a.pdf 2.
Načelno znam kako bih riješila zadatak , ali imam problema s bazama u kojim je A zadan i s ovom {A(1),A(t),A(t^2)}
...eto,ako je tko voljan pomoći,hvala :)[/quote]
[url=http://degiorgi.math.hr/forum/viewtopic.php?p=115709#115709]rjesenje...[/url]
| NeonBlack (napisa): | http://web.math.hr/nastava/la/kolokviji/08-09/la2/kol1a.pdf 2.
Načelno znam kako bih riješila zadatak , ali imam problema s bazama u kojim je A zadan i s ovom {A(1),A(t),A(t^2)}
...eto,ako je tko voljan pomoći,hvala  |
rjesenje...
_________________
Mario Berljafa
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 20:28 sub, 13. 3. 2010 Naslov: Postano: 20:28 sub, 13. 3. 2010 Naslov: |
    |
|
|
Neka je lin.operator A E L(R4) dan formulom A(x1,x2,x3,x4)=(x2+2(x3)-x4, x1+x3, 2(x1)+x2, x1). Odredite A(e´) ako je (e´) ={(1,1,1,1), (1,1,1,0), (1,1,0,0), (1,0,0,0)}.Pokažite da je A regularan i odredite mu inverzni operator.
Ja sam ovako rješila pa bi molila samo da mi netko provjeri,jer još uvijek nisam na ti s tim:
A(e´) = I(e,e´)^(-1)A(e)I(e,e´)
I(e,e´)=
1 1 1 1
1 1 1 0
1 1 0 0
1 0 0 0
A(e)=
0 1 2 -1
1 0 1 0
2 1 0 0
1 0 0 0
=> A(e´) =
1 1 1 1
3 3 3 0
0 0 -1 -1
0 1 0 -1
ako je regularan,onda mu je bilo koja matrica operatora invertibilna?
i ako može netko riješiti za inverzni operator?
Neka je lin.operator A E L(R4) dan formulom A(x1,x2,x3,x4)=(x2+2(x3)-x4, x1+x3, 2(x1)+x2, x1). Odredite A(e´) ako je (e´) ={(1,1,1,1), (1,1,1,0), (1,1,0,0), (1,0,0,0)}.Pokažite da je A regularan i odredite mu inverzni operator.
Ja sam ovako rješila pa bi molila samo da mi netko provjeri,jer još uvijek nisam na ti s tim:
A(e´) = I(e,e´)^(-1)A(e)I(e,e´)
I(e,e´)=
1 1 1 1
1 1 1 0
1 1 0 0
1 0 0 0
A(e)=
0 1 2 -1
1 0 1 0
2 1 0 0
1 0 0 0
=> A(e´) =
1 1 1 1
3 3 3 0
0 0 -1 -1
0 1 0 -1
ako je regularan,onda mu je bilo koja matrica operatora invertibilna?
i ako može netko riješiti za inverzni operator?
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
 Postano: 16:58 ned, 14. 3. 2010 Naslov: Postano: 16:58 ned, 14. 3. 2010 Naslov: |
    |
|
|
moze mala pomoc oko zadatka... trebam nac matrice operatora A:R^3->P1 A(x,y,z)=x+y+z+xt u paru baza e'={(-1,1-0),(1,0,1),(0,0,1)} i f'={1+t,1-2t}...
i sad ja sam uvela e kao kanonska baza za R^3 i f kao kanonska baza za P i imam da je A(f',e')=T(f',f)A(f)I(f,e') i sad mi treba mala pomoc oko matrica za A(f) i I(f,e')...
za A(f) sam dobila 1 1 1
1 0 0
ali nisam sigurna dali je to dobro... a za T(f,e') neznam ni kako bi pocela pa dali bi mi neko mogao pomoci??
moze mala pomoc oko zadatka... trebam nac matrice operatora A:R^3->P1 A(x,y,z)=x+y+z+xt u paru baza e'={(-1,1-0),(1,0,1),(0,0,1)} i f'={1+t,1-2t}...
i sad ja sam uvela e kao kanonska baza za R^3 i f kao kanonska baza za P i imam da je A(f',e')=T(f',f)A(f)I(f,e') i sad mi treba mala pomoc oko matrica za A(f) i I(f,e')...
za A(f) sam dobila 1 1 1
1 0 0
ali nisam sigurna dali je to dobro... a za T(f,e') neznam ni kako bi pocela pa dali bi mi neko mogao pomoci??
|
|
| [Vrh] |
|
|







