| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
gego
Forumaš(ica)

Pridružen/a: 20. 09. 2009. (21:10:55)
Postovi: (1B)16
Spol: 
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
 Postano: 19:49 sri, 17. 3. 2010 Naslov: Postano: 19:49 sri, 17. 3. 2010 Naslov: |
    |
|
|
za prvi dio zadatka:
[latex]\Rightarrow:[/latex] A je surjektivan, a budući da je [latex]A{\in}L(V)[/latex], riječ je o izomorfizmu( [latex] x{\in}ImA, {\forall}x{\in}V)[/latex] i da bude zadovoljena jednakost [latex]BoA=0, B[/latex] je nužno nul-operator jer je to jedini koji prevodi sve vektore u nulu.
[latex]\Leftarrow:[/latex]Nužno je [latex]KerA={\{}0{\}}[/latex], jer u suprotnom, [latex]{\exists}x{\in}V, x{\not=}0 \ t.d.\ Ax=0, pa Bx[/latex] nije nužno 0, dakle [latex]B{\not=}0[/latex], što je kontradikcija.
Očita je posljedica toga da je [latex]ImA=KerB[/latex], a isto tako i za drugi dio zadatka.
za prvi dio zadatka:
 A je surjektivan, a budući da je A je surjektivan, a budući da je 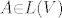 , riječ je o izomorfizmu( , riječ je o izomorfizmu( 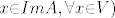 i da bude zadovoljena jednakost i da bude zadovoljena jednakost 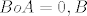 je nužno nul-operator jer je to jedini koji prevodi sve vektore u nulu. je nužno nul-operator jer je to jedini koji prevodi sve vektore u nulu.
 Nužno je Nužno je 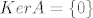 , jer u suprotnom, , jer u suprotnom, 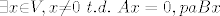 nije nužno 0, dakle nije nužno 0, dakle 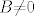 , što je kontradikcija. , što je kontradikcija.
Očita je posljedica toga da je  , a isto tako i za drugi dio zadatka. , a isto tako i za drugi dio zadatka.
|
|
| [Vrh] |
|
gego
Forumaš(ica)

Pridružen/a: 20. 09. 2009. (21:10:55)
Postovi: (1B)16
Spol: 
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 4:06 čet, 18. 3. 2010 Naslov: Postano: 4:06 čet, 18. 3. 2010 Naslov: |
    |
|
|
[quote="gego"]Neka su A,B : V-->V lin.op. Treba dokazati
a) B je injektivan <--> (BA=0 ->A=0)[/quote]
--> Uzmi x iz V proizvoljan. Onda je BAx=0. B je injektivan, pa je Ax=0. Znaci, za svaki x iz V je Ax=0, pa je A=0.
<-- Pretpostavi da B nije injektican, tj postoji y razlicit od 0 iz V takav da je By=0. Neka je A projekcija V na potprostor razapet s y (npr. nadopuni y do baze, s y2,y3,..., i neka je Ay=y, Ayi=0). Onda je BA=0 (npr provjeri na bazi ovoj otprije), pa je po pretpostavci A=0. Medutim, Ay=y nije 0, sto je kontradikcija.
[quote="gego"]....
i zasto bi vrijedilo ImA=KerB ?[/quote]
Injektivan B znaci KerB=0, a A=0 znaci ImA=0.
U prethodnom slucaju su i KerB i ImA jednaki V.
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="genchy"]A je surjektivan, a budući da je [latex]A{\in}L(V)[/latex], riječ je o izomorfizmu[/quote]
Vjerojatno nije bitno za zadatak, ali ovdje ne moras koristiti da je A izomorfizam. Dovoljno je stvarno da je surjektivan (ideja: A pogodi sve, pa ako je BA=0 onda B ubije sve).
Razlog zasto to spominjem je jer ove ekvivalencije izgledaju kao da vrijede i na vekt prostorima koji nisu konacno dimenzionalni, a "svaka injekcija je izomorfizam" vrijedi samo za kondim prostore...
| gego (napisa): | Neka su A,B : V→V lin.op. Treba dokazati
a) B je injektivan ↔ (BA=0 →A=0) |
→ Uzmi x iz V proizvoljan. Onda je BAx=0. B je injektivan, pa je Ax=0. Znaci, za svaki x iz V je Ax=0, pa je A=0.
← Pretpostavi da B nije injektican, tj postoji y razlicit od 0 iz V takav da je By=0. Neka je A projekcija V na potprostor razapet s y (npr. nadopuni y do baze, s y2,y3,..., i neka je Ay=y, Ayi=0). Onda je BA=0 (npr provjeri na bazi ovoj otprije), pa je po pretpostavci A=0. Medutim, Ay=y nije 0, sto je kontradikcija.
| gego (napisa): | ....
i zasto bi vrijedilo ImA=KerB ? |
Injektivan B znaci KerB=0, a A=0 znaci ImA=0.
U prethodnom slucaju su i KerB i ImA jednaki V.
Added after 3 minutes:
| genchy (napisa): | A je surjektivan, a budući da je 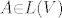 , riječ je o izomorfizmu , riječ je o izomorfizmu |
Vjerojatno nije bitno za zadatak, ali ovdje ne moras koristiti da je A izomorfizam. Dovoljno je stvarno da je surjektivan (ideja: A pogodi sve, pa ako je BA=0 onda B ubije sve).
Razlog zasto to spominjem je jer ove ekvivalencije izgledaju kao da vrijede i na vekt prostorima koji nisu konacno dimenzionalni, a "svaka injekcija je izomorfizam" vrijedi samo za kondim prostore...
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
 Postano: 20:24 pon, 22. 3. 2010 Naslov: Postano: 20:24 pon, 22. 3. 2010 Naslov: |
    |
|
|
Neka je linearni operator A:R^4 -> R^4. U kanonskoj bazi (e)={e_1, e_2, e_3, e_4} ima matricu Dimensions[{{1, 2, 0, 1}, {3, 0, -1, 2}, {2, 5, 3, 1}, {1, 2, 1, 3}}] . Neka je (e')={e'_1, e'_2, e'_3, e'_4} baza za R^4 zadana sa e'_1=e_1, e'_2=e_1 + e_2, e'_3=e_1 + e_2 + e_3, e'_4=e_1 + e_2 + e_3+e_4 ; a (e'')={e''_1, e''_2, e''_3, e''_4}, gdje je e''_1=e_1, e''_2=e_2, e''_3=e_4, e''_4=e_3: a) Za x=(1,-1,2,1) odredi A(x)(e), te A(x)(e'); b) y(e')=(-1, -3, 6, -8 ) (jednostupcana matrica, koju nisam znao napisati u ovom cudu). Odredite A(y)(e). c) Odredite matricu prijelaza iz (e') u (e'') i A(e'').
Kod matrice A(e) podzagrade idu po retcima... dakle 1. red je (1, 2, 0, 1), itd.
Konkretno mi nije jasno u ovom zadatku je li A(x)(e) prikaz zapravo jednostupcane matrice koja ima redom koeficijente u linearnoj kombinaciji kanonske baze Ax= 0*e1 + 3*e2+ 4*e3+4*e4 (jer tako A djeluje na x kad se x rastavi u kanonskoj bazi (nadam se da je racun bio dobar)) (0,3,4,4) ili je to nesto drugo... Druga stvar koju zelim pitati je da li je A(x)(e') zapravo prikaz jednostupcane matrice Ax u bazi e'... b) Da li je jednostupcana matirca y(e')=(-1, -3, 6 , -8 ) zapravo y(e')=-e'_1-3*e'_2+6*e'_3-8*e'_4. c) Ne pada mi na ideju kako bi to uopce mogao prikazati osim da prvo nadjem I(e',e) pa I(e, e'')=(I(e'', e))^-1 i onda ih pomnozim
Neka je linearni operator A:R^4 → R^4. U kanonskoj bazi (e)={e_1, e_2, e_3, e_4} ima matricu Dimensions[{{1, 2, 0, 1}, {3, 0, -1, 2}, {2, 5, 3, 1}, {1, 2, 1, 3}}] . Neka je (e')={e'_1, e'_2, e'_3, e'_4} baza za R^4 zadana sa e'_1=e_1, e'_2=e_1 + e_2, e'_3=e_1 + e_2 + e_3, e'_4=e_1 + e_2 + e_3+e_4 ; a (e'')={e''_1, e''_2, e''_3, e''_4}, gdje je e''_1=e_1, e''_2=e_2, e''_3=e_4, e''_4=e_3: a) Za x=(1,-1,2,1) odredi A(x)(e), te A(x)(e'); b) y(e')=(-1, -3, 6, -8 ) (jednostupcana matrica, koju nisam znao napisati u ovom cudu). Odredite A(y)(e). c) Odredite matricu prijelaza iz (e') u (e'') i A(e'').
Kod matrice A(e) podzagrade idu po retcima... dakle 1. red je (1, 2, 0, 1), itd.
Konkretno mi nije jasno u ovom zadatku je li A(x)(e) prikaz zapravo jednostupcane matrice koja ima redom koeficijente u linearnoj kombinaciji kanonske baze Ax= 0*e1 + 3*e2+ 4*e3+4*e4 (jer tako A djeluje na x kad se x rastavi u kanonskoj bazi (nadam se da je racun bio dobar)) (0,3,4,4) ili je to nesto drugo... Druga stvar koju zelim pitati je da li je A(x)(e') zapravo prikaz jednostupcane matrice Ax u bazi e'... b) Da li je jednostupcana matirca y(e')=(-1, -3, 6 , -8 ) zapravo y(e')=-e'_1-3*e'_2+6*e'_3-8*e'_4. c) Ne pada mi na ideju kako bi to uopce mogao prikazati osim da prvo nadjem I(e',e) pa I(e, e'')=(I(e'', e))^-1 i onda ih pomnozim
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
 Postano: 21:30 pon, 22. 3. 2010 Naslov: Postano: 21:30 pon, 22. 3. 2010 Naslov: |
    |
|
|
Da, [latex](Ax)(e)[/latex] je prikaz kako operator A djeluje na x, tehnički to je množenje matrica, jer [latex](Ax)(e)=A(e){\cdot}x(e)[/latex], a to je upravo [latex] \begin{pmatrix} 0 \\ 3 \\ 4 \\ 4 \end{pmatrix} [/latex], tako je [latex](Ax)(e')\;=\;A(e'){\cdot}x(e')[/latex] jednostupčana matrica i svakako koristiš matrice prijelaza, [latex] A(e')\; =\; I(e',e){\cdot}A(e){\cdot}I(e,e') [/latex] i mislim da bi trebao dobit [latex]\;\begin {pmatrix} -2 & 0 & 1 & 0 \\ 1 & -4 & -8 & -7 \\ 1 & 4 & 6 & 4 \\ 1 & 3 & 4 & 7 \end{pmatrix}[/latex], a [latex]x(e')=I(e',e){\cdot}x(e)[/latex]. Tu se dobije [latex]\begin {pmatrix} -3 \\ -1 \\ 0 \\ 4 \end{pmatrix}[/latex]. Vezana za b), dobro si raspisao, to je po definiciji matrični prikaz vektora y u bazi e', no matrični prikazi općenito daju upravo tu prednost da ne moramo raspisivati vektor ili djelovanje operatora u nekoj bazi, nego ga automatski koristimo pomoću matrica i njenih operacija, pa tako i za y, dobijemo njegov prikaz u bazi e (identično kao i za x) te imamo čisto množenje matrica[latex](Ay)(e)\;=\;A(e){\cdot}y(e)[/latex]. Za c) ti ne treba više [latex]I(e',e)[/latex], nego bi iz matice [latex]I(e,e'')[/latex] trebao izvlačiti inverz, no u ovom slučaju je jednostavna baza e'', pa direktno upišeš [latex]I(e'',e)[/latex], dakle prikaz svakog vektora iz baze e u bazi e''. Kasnije uvrstiš u formulu isto kao u a), samo umjesto e' ide e'', i dobiješ [latex]A(e'')[/latex]. Valjda nisam pogriješio u računu, mislim da je ok. . .
Da, 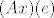 je prikaz kako operator A djeluje na x, tehnički to je množenje matrica, jer je prikaz kako operator A djeluje na x, tehnički to je množenje matrica, jer 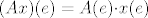 , a to je upravo , a to je upravo 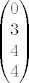 , tako je , tako je 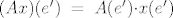 jednostupčana matrica i svakako koristiš matrice prijelaza, jednostupčana matrica i svakako koristiš matrice prijelaza, 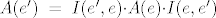 i mislim da bi trebao dobit i mislim da bi trebao dobit 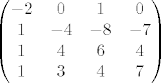 , a , a 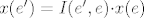 . Tu se dobije . Tu se dobije  . Vezana za b), dobro si raspisao, to je po definiciji matrični prikaz vektora y u bazi e', no matrični prikazi općenito daju upravo tu prednost da ne moramo raspisivati vektor ili djelovanje operatora u nekoj bazi, nego ga automatski koristimo pomoću matrica i njenih operacija, pa tako i za y, dobijemo njegov prikaz u bazi e (identično kao i za x) te imamo čisto množenje matrica . Vezana za b), dobro si raspisao, to je po definiciji matrični prikaz vektora y u bazi e', no matrični prikazi općenito daju upravo tu prednost da ne moramo raspisivati vektor ili djelovanje operatora u nekoj bazi, nego ga automatski koristimo pomoću matrica i njenih operacija, pa tako i za y, dobijemo njegov prikaz u bazi e (identično kao i za x) te imamo čisto množenje matrica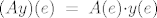 . Za c) ti ne treba više . Za c) ti ne treba više 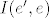 , nego bi iz matice , nego bi iz matice 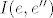 trebao izvlačiti inverz, no u ovom slučaju je jednostavna baza e'', pa direktno upišeš trebao izvlačiti inverz, no u ovom slučaju je jednostavna baza e'', pa direktno upišeš 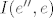 , dakle prikaz svakog vektora iz baze e u bazi e''. Kasnije uvrstiš u formulu isto kao u a), samo umjesto e' ide e'', i dobiješ , dakle prikaz svakog vektora iz baze e u bazi e''. Kasnije uvrstiš u formulu isto kao u a), samo umjesto e' ide e'', i dobiješ 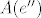 . Valjda nisam pogriješio u računu, mislim da je ok. . . . Valjda nisam pogriješio u računu, mislim da je ok. . .
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 21:31 pon, 22. 3. 2010 Naslov: Postano: 21:31 pon, 22. 3. 2010 Naslov: |
    |
|
|
Bilo bi naprosto divno kad bi svi ljudi pisali u latex-u :). Na primjer, [latex]A(e) = \left[ \begin{matrix} 1 & 2 & 0 & 1 \\ 3 & 0 & -1 & 2 \\ 2 & 5 & 3 & 1 \\ 1 & 2 & 1 & 3 \end{matrix} \right][/latex]. No, pustimo moje jade...
[quote="ankovacic"]Konkretno mi nije jasno u ovom zadatku je li A(x)(e) prikaz zapravo jednostupcane matrice koja ima redom koeficijente u linearnoj kombinaciji kanonske baze Ax= 0*e1 + 3*e2+ 4*e3+4*e4 (jer tako A djeluje na x kad se x rastavi u kanonskoj bazi (nadam se da je racun bio dobar)) (0,3,4,4) ili je to nesto drugo...[/quote]
Rezultat ti je dobar, no to možeš jednostavno po formuli [latex](Ax)(e)=A(e)x(e)[/latex] (množenje matrica).
[quote="ankovacic"]Druga stvar koju zelim pitati je da li je A(x)(e') zapravo prikaz jednostupcane matrice Ax u bazi e'...[/quote]
Je. Za to možeš iskoristiti matricu prijelaza, točnije [latex](Ax)(e') = I(e',e)(Ax)(e)[/latex].
[quote="ankovacic"]b) Da li je jednostupcana matirca y(e')=(-1, -3, 6 , -8 ) zapravo y(e')=-e'_1-3*e'_2+6*e'_3-8*e'_4.[/quote]
Je, ali i tu možeš iskoristiti matrice prijelaza, pa ti ne trebaju ove lin. komb.
[quote="ankovacic"]c) Ne pada mi na ideju kako bi to uopce mogao prikazati osim da prvo nadjem I(e',e) pa I(e, e'')=(I(e'', e))^-1 i onda ih pomnozim[/quote]
Pa da, nema potrebe izmišljati nešto novo. Imaš formulu A(e'') = I(e'',e) A(e) I(e,e''), iskoristi je :).
Ah, za minutu... :)
Bilo bi naprosto divno kad bi svi ljudi pisali u latex-u  . Na primjer, . Na primjer,  . No, pustimo moje jade... . No, pustimo moje jade...
| ankovacic (napisa): | | Konkretno mi nije jasno u ovom zadatku je li A(x)(e) prikaz zapravo jednostupcane matrice koja ima redom koeficijente u linearnoj kombinaciji kanonske baze Ax= 0*e1 + 3*e2+ 4*e3+4*e4 (jer tako A djeluje na x kad se x rastavi u kanonskoj bazi (nadam se da je racun bio dobar)) (0,3,4,4) ili je to nesto drugo... |
Rezultat ti je dobar, no to možeš jednostavno po formuli 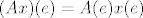 (množenje matrica). (množenje matrica).
| ankovacic (napisa): | | Druga stvar koju zelim pitati je da li je A(x)(e') zapravo prikaz jednostupcane matrice Ax u bazi e'... |
Je. Za to možeš iskoristiti matricu prijelaza, točnije 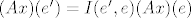 . .
| ankovacic (napisa): | | b) Da li je jednostupcana matirca y(e')=(-1, -3, 6 , -8 ) zapravo y(e')=-e'_1-3*e'_2+6*e'_3-8*e'_4. |
Je, ali i tu možeš iskoristiti matrice prijelaza, pa ti ne trebaju ove lin. komb.
| ankovacic (napisa): | | c) Ne pada mi na ideju kako bi to uopce mogao prikazati osim da prvo nadjem I(e',e) pa I(e, e'')=(I(e'', e))^-1 i onda ih pomnozim |
Pa da, nema potrebe izmišljati nešto novo. Imaš formulu A(e'') = I(e'',e) A(e) I(e,e''), iskoristi je  . .
Ah, za minutu... 
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 17:43 uto, 23. 3. 2010 Naslov: Postano: 17:43 uto, 23. 3. 2010 Naslov: |
    |
|
|
[quote="ankovacic"]kako da se naucim pisati matrice i te stvari..[/quote]
To se, kao i programiranje, najbolje uči kodirajući. Skini si [url=http://miktex.org/2.8/setup]MiKTeX[/url] i kreni :). Za učenje ti može koristiti [url=http://web.studenti.math.hr/~nesi/latex/reference/berit%20givens%20-%20latex%20notes.pdf]ovo[/url]. Još puno lijepih stvari imaš na [url]http://web.studenti.math.hr/~nesi/latex/[/url].
[quote="ankovacic"]pisao bi i ja grčka slova kak spada[/quote]
To je barem jednostavno: [latex]\alpha, \beta, \gamma, \ldots[/latex](stavi strelicu na zelenog "smajlića" gore desno da vidiš kako to zapravo izgleda). Za ostale česte znakove, pogledaj [url=http://web.studenti.math.hr/~nesi/latex/reference/latexsymbols-4a4.pdf]ovdje[/url]. U text editoru bi matematički tekst pisao sa dolarima, npr. $\alpha$.
| ankovacic (napisa): | | kako da se naucim pisati matrice i te stvari.. |
To se, kao i programiranje, najbolje uči kodirajući. Skini si MiKTeX i kreni  . Za učenje ti može koristiti ovo. Još puno lijepih stvari imaš na http://web.studenti.math.hr/~nesi/latex/. . Za učenje ti može koristiti ovo. Još puno lijepih stvari imaš na http://web.studenti.math.hr/~nesi/latex/.
| ankovacic (napisa): | | pisao bi i ja grčka slova kak spada |
To je barem jednostavno: 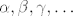 (stavi strelicu na zelenog "smajlića" gore desno da vidiš kako to zapravo izgleda). Za ostale česte znakove, pogledaj ovdje. U text editoru bi matematički tekst pisao sa dolarima, npr. $\alpha$. (stavi strelicu na zelenog "smajlića" gore desno da vidiš kako to zapravo izgleda). Za ostale česte znakove, pogledaj ovdje. U text editoru bi matematički tekst pisao sa dolarima, npr. $\alpha$.
|
|
| [Vrh] |
|
|










