| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
marichuy
Forumaš(ica)

Pridružen/a: 11. 11. 2009. (21:52:56)
Postovi: (26)16
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 4:20 čet, 18. 3. 2010 Naslov: Postano: 4:20 čet, 18. 3. 2010 Naslov: |
    |
|
|
[quote="genchy"]S obzirom da je rijec o neparnoj funkciji...[/quote]
sin(x^2) je parna funkcija.
Najjednostavniji nacin koji meni pada na pamet je Taylorov red, ali ne znam jel to vec obradeno gradivo:
sin y= y -y^3/3! +y^5/5! - y^7/7! +.... Uglavnom, jedini koeficijenti koji su ne 0 su us neparne potencije.
Sad ubacis y=x^2 pa opet razvijes oko 0, tj samo uvrstis u ono gore:
sin x^2 = x^2 -x^6/3! +x^{10}/5! - x^{14}/7! +...
Koeficijent us x^n je n-ta derivacija funkcije sin(x^2) podijeljena sa n!, a jednini ne 0 su parni brojevi koji nisu djeljivi s 4. Dakle, koeficijent uz x^{100} je 0, pa tako i derivacija.
| genchy (napisa): | | S obzirom da je rijec o neparnoj funkciji... |
sin(x^2) je parna funkcija.
Najjednostavniji nacin koji meni pada na pamet je Taylorov red, ali ne znam jel to vec obradeno gradivo:
sin y= y -y^3/3! +y^5/5! - y^7/7! +.... Uglavnom, jedini koeficijenti koji su ne 0 su us neparne potencije.
Sad ubacis y=x^2 pa opet razvijes oko 0, tj samo uvrstis u ono gore:
sin x^2 = x^2 -x^6/3! +x^{10}/5! - x^{14}/7! +...
Koeficijent us x^n je n-ta derivacija funkcije sin(x^2) podijeljena sa n!, a jednini ne 0 su parni brojevi koji nisu djeljivi s 4. Dakle, koeficijent uz x^{100} je 0, pa tako i derivacija.
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
marichuy
Forumaš(ica)

Pridružen/a: 11. 11. 2009. (21:52:56)
Postovi: (26)16
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
lanek
Forumaš(ica)


Pridružen/a: 06. 10. 2009. (21:51:48)
Postovi: (51)16
Spol: 
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
lanek
Forumaš(ica)


Pridružen/a: 06. 10. 2009. (21:51:48)
Postovi: (51)16
Spol: 
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
amimica
Forumaš(ica)

Pridružen/a: 14. 04. 2004. (15:40:42)
Postovi: (CA)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
MI
Forumaš(ica)

Pridružen/a: 11. 11. 2009. (20:54:30)
Postovi: (26)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 12:49 sri, 7. 4. 2010 Naslov: Postano: 12:49 sri, 7. 4. 2010 Naslov: |
    |
|
|
Po Leibnizu slijedi [latex]f^{(n)}(x) = x (Arsh\,x)^{(n)} + n (Arsh\,x)^{(n-1)}[/latex]. Kad uvrstimo [latex]x = 0[/latex], dobivamo [latex]f^{(n)}(0) = n (Arsh\,x)^{(n-1)}|_{x=0}[/latex] (to znači da treba [latex]n-1[/latex] puta derivirati Arsh x, pa tek onda uvrstiti 0). Dakle, zadatak se svodi na nalaženje 99-te derivacije od Arsh x, što je vrlo slično (kad se jednom derivira Arsh x) onom dva posta gore.
[url=http://www.wolframalpha.com/input/?i=%28D%28x+Arcsinh%28x%29%2C{x%2C100}%29%2F.x-%3E0%29%2B100%2897!!%29^2]Konačno rješenje[/url]: [latex]-100(97!!)^2[/latex].
Po Leibnizu slijedi 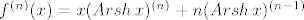 . Kad uvrstimo . Kad uvrstimo  , dobivamo , dobivamo 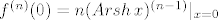 (to znači da treba (to znači da treba 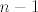 puta derivirati Arsh x, pa tek onda uvrstiti 0). Dakle, zadatak se svodi na nalaženje 99-te derivacije od Arsh x, što je vrlo slično (kad se jednom derivira Arsh x) onom dva posta gore. puta derivirati Arsh x, pa tek onda uvrstiti 0). Dakle, zadatak se svodi na nalaženje 99-te derivacije od Arsh x, što je vrlo slično (kad se jednom derivira Arsh x) onom dva posta gore.
Konačno rješenje: 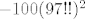 . .
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
|












