Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

zadatak matrični zapis lin. op.
WWW:
Idite na Prethodno  1, 2
Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Linearna algebra 1 & 2 (za inženjerske smjerove)
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
Genaro
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: muško
Sarma = la pohva - posuda
18 = 18 - 0
Lokacija: Zagreb
PostPostano: 22:02 sub, 3. 4. 2010    Naslov: Citirajte i odgovorite
Da, stvarno :D

Ok, kad sam već krenuo onda, pitat ću i sljedeće 2006. god. A grupa 2 zadatak pod c. nisam siguran kako točno prikazati, iako je vjerojatno jednostavno:
http://web.math.hr/nastava/la/kolokviji/05-06/la2/kol1a.pdf

Mogao bih i koje teorijsko!
Recimo evo od prošle godine;

Dokažite: Ako je F matrični zapis regularnog operatora f onda je [latex]F^{-1}[/latex] matrica njegova inverza [latex]f^{-1}.[/latex]
Da, stvarno Very Happy

Ok, kad sam već krenuo onda, pitat ću i sljedeće 2006. god. A grupa 2 zadatak pod c. nisam siguran kako točno prikazati, iako je vjerojatno jednostavno:
http://web.math.hr/nastava/la/kolokviji/05-06/la2/kol1a.pdf

Mogao bih i koje teorijsko!
Recimo evo od prošle godine;

Dokažite: Ako je F matrični zapis regularnog operatora f onda je matrica njegova inverza


[Vrh]
Korisnički profil Pošaljite privatnu poruku
pmli
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: muško
Sarma = la pohva - posuda
197 = 203 - 6
PostPostano: 22:17 sub, 3. 4. 2010    Naslov: Citirajte i odgovorite
[quote="Genaro"]Ok, kad sam već krenuo onda, pitat ću i sljedeće 2006. god. A grupa 2 zadatak pod c. nisam siguran kako točno prikazati, iako je vjerojatno jednostavno:
http://web.math.hr/nastava/la/kolokviji/05-06/la2/kol1a.pdf[/quote]
[latex](f(p))(C') = f(C',B') \cdot p(B') = f(C',B') \cdot I_{\mathcal{P}_2}(B',B) \cdot p(B)[/latex]
[quote="Genaro"]Dokažite: Ako je F matrični zapis regularnog operatora f onda je [latex]F^{-1}[/latex] matrica njegova inverza [latex]f^{-1}.[/latex][/quote]
Ajmo koristiti standardne oznake. Neka je [latex]e[/latex] baza za domenu/kodomenu of [latex]f[/latex].Treba pokazati da [latex][f]_e^e \cdot [f^{-1}]_e^e = I[/latex]. To je jednostavno jer imamo općenitiji teorem. Za njegov dokaz, pogledaj [url=http://web.math.hr/nastava/la/razno/web_LA_ch5_student.pdf]prof. Bakićeve skripte, propozicija 1.4.10., str. 18[/url]
Genaro (napisa):
Ok, kad sam već krenuo onda, pitat ću i sljedeće 2006. god. A grupa 2 zadatak pod c. nisam siguran kako točno prikazati, iako je vjerojatno jednostavno:
http://web.math.hr/nastava/la/kolokviji/05-06/la2/kol1a.pdf


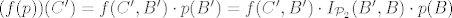
Genaro (napisa):
Dokažite: Ako je F matrični zapis regularnog operatora f onda je 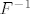matrica njegova inverza

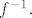Ajmo koristiti standardne oznake. Neka je baza za domenu/kodomenu of .Treba pokazati da 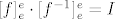. To je jednostavno jer imamo općenitiji teorem. Za njegov dokaz, pogledaj prof. Bakićeve skripte, propozicija 1.4.10., str. 18


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Genaro
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: muško
Sarma = la pohva - posuda
18 = 18 - 0
Lokacija: Zagreb
PostPostano: 22:26 sub, 3. 4. 2010    Naslov: Citirajte i odgovorite
E super, to bi bilo to zasad.
Zahvaljujem.
E super, to bi bilo to zasad.
Zahvaljujem.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
suza
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
7 = 8 - 1
PostPostano: 14:20 ned, 4. 4. 2010    Naslov: Citirajte i odgovorite
[quote="pmli"]Što to znači ? Operator je zadan kako djeluje na proizvoljan vektor, iz čega se lako isčita matrični prikaz u paru kanonskih baza (a dio zadatka): [latex]f(C,B) = \begin{bmatrix} 2 & 3 \\ 1 & 2 \\ 1 & 1 \end{bmatrix}[/latex].[/quote]

Zašto je matrica f(C,B) dim 3x2? Zar ne bi trebala biti 2x3?
[latex]f(C,B) = \begin{bmatrix} 2 & 1 & 1 \\ 3 & 2 & 1 \end{bmatrix}[/latex].
pmli (napisa):
Što to znači ? Operator je zadan kako djeluje na proizvoljan vektor, iz čega se lako isčita matrični prikaz u paru kanonskih baza (a dio zadatka): .


Zašto je matrica f(C,B) dim 3x2? Zar ne bi trebala biti 2x3?
.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
pmli
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: muško
Sarma = la pohva - posuda
197 = 203 - 6
PostPostano: 16:10 ned, 4. 4. 2010    Naslov: Citirajte i odgovorite
[quote="suza"][quote="pmli"]Što to znači ? Operator je zadan kako djeluje na proizvoljan vektor, iz čega se lako isčita matrični prikaz u paru kanonskih baza (a dio zadatka): [latex]f(C,B) = \begin{bmatrix} 2 & 3 \\ 1 & 2 \\ 1 & 1 \end{bmatrix}[/latex].[/quote]

Zašto je matrica f(C,B) dim 3x2? Zar ne bi trebala biti 2x3?
[latex]f(C,B) = \begin{bmatrix} 2 & 1 & 1 \\ 3 & 2 & 1 \end{bmatrix}[/latex].[/quote]
Zavisi koju grupu rješavaš :).
suza (napisa):
pmli (napisa):
Što to znači ? Operator je zadan kako djeluje na proizvoljan vektor, iz čega se lako isčita matrični prikaz u paru kanonskih baza (a dio zadatka): .


Zašto je matrica f(C,B) dim 3x2? Zar ne bi trebala biti 2x3?
.

Zavisi koju grupu rješavaš Smile.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
suza
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
7 = 8 - 1
PostPostano: 17:39 ned, 4. 4. 2010    Naslov: Citirajte i odgovorite
..pa da :oops: gledala sam drugu grupu

Imam pitanje vezano uz drugi dio 3. zadatka.
http://web.math.hr/nastava/la/kolokviji/05-06/la2/kol1a.pdf
Kako prikazati f* u dualnoj bazi B*? Rješavali smo slične zadatke na vježbama, ali tada smo znali bazu B. Malo mi je sve to zbunjujuće. Može li mi netko objasniti kako riješiti taj dio zadatka?
..pa da Embarassed gledala sam drugu grupu

Imam pitanje vezano uz drugi dio 3. zadatka.
http://web.math.hr/nastava/la/kolokviji/05-06/la2/kol1a.pdf
Kako prikazati f* u dualnoj bazi B*? Rješavali smo slične zadatke na vježbama, ali tada smo znali bazu B. Malo mi je sve to zbunjujuće. Može li mi netko objasniti kako riješiti taj dio zadatka?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
pmli
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: muško
Sarma = la pohva - posuda
197 = 203 - 6
PostPostano: 17:52 ned, 4. 4. 2010    Naslov: Citirajte i odgovorite
Objašnjavah to [url=http://degiorgi.math.hr/forum/viewtopic.php?t=14789&postdays=0&postorder=asc&&start=0]ovdje[/url], 4. post računajući od zadnjeg.
Objašnjavah to ovdje, 4. post računajući od zadnjeg.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Gost
PostPostano: 19:21 ned, 4. 4. 2010    Naslov: Citirajte i odgovorite
[quote="Genaro"]2. zadatak 2008 A grupa: http://web.math.hr/nastava/la/kolokviji/07-08/la2/kol1a.pdf

Ja sam to rješavao na sljedeći način, zanima me valja li štogod:

[latex]A(f'',e'')=I(f'',f')\cdot A(f',e')\cdot I(e',e'')=
\\
\\ = \left[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{matrix}\right]^{-1} \cdot \left[\begin{matrix} 1 & 1 & 1 & 2 \\ 2 & 0 & 1 & 0 \\ 1 & 1 & 0 & 2 \\ 1 & 1 & 1 & 2 \end{matrix} \right] \cdot \left[ \begin{matrix} 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\0 & 0 & 0 & -1 \\ 0 & 1 & 1 & 1 \end{matrix} \right]^{-1}=...
[/latex]

Prvu bazu za domenu sam označio sa (e'), drugu sa (e''), prvu bazu za kodomenu sa (f'), a drugu sa (f''). Samo me zanima jeli postupak korektan.

Također, za ovaj dio sa izomorfizmom, nisam stoposto siguran na koji način se u ovom zadatku dokaže pa bih molio pomoć.[/quote]

zašto se računa inverz od zadnje matrice?
Genaro (napisa):
2. zadatak 2008 A grupa: http://web.math.hr/nastava/la/kolokviji/07-08/la2/kol1a.pdf

Ja sam to rješavao na sljedeći način, zanima me valja li štogod:



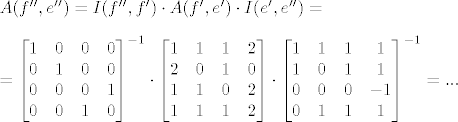
Prvu bazu za domenu sam označio sa (e'), drugu sa (e''), prvu bazu za kodomenu sa (f'), a drugu sa (f''). Samo me zanima jeli postupak korektan.

Također, za ovaj dio sa izomorfizmom, nisam stoposto siguran na koji način se u ovom zadatku dokaže pa bih molio pomoć.


zašto se računa inverz od zadnje matrice?


[Vrh]
Genaro
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: muško
Sarma = la pohva - posuda
18 = 18 - 0
Lokacija: Zagreb
PostPostano: 19:32 ned, 4. 4. 2010    Naslov: Citirajte i odgovorite
Ja sam na taj način računao jer mi je bilo lakše odmah prikazati [latex] I(e'',e')[/latex] zbog odabira baza, pa sam zato morao inverz, naravno možeš i direktno računati [latex]I(e'.e'')[/latex], dođe na isto.
Ja sam na taj način računao jer mi je bilo lakše odmah prikazati zbog odabira baza, pa sam zato morao inverz, naravno možeš i direktno računati , dođe na isto.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
dina12
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 21. 11. 2009. (17:20:26)
Postovi: (18)16
Sarma = la pohva - posuda
4 = 5 - 1
PostPostano: 16:33 pon, 5. 4. 2010    Naslov: Citirajte i odgovorite
Može rješenje 1. i 2.zadatka prošlogodišnjeg kolokvija B.grupa?
http://web.math.hr/nastava/la/kolokviji/07-08/la2/kol1b.pdf
Može rješenje 1. i 2.zadatka prošlogodišnjeg kolokvija B.grupa?
http://web.math.hr/nastava/la/kolokviji/07-08/la2/kol1b.pdf


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Linearna algebra 1 & 2 (za inženjerske smjerove) Vremenska zona: GMT + 01:00.
Idite na Prethodno  1, 2
Stranica 2 / 2.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan