| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 13:56 sub, 10. 4. 2010 Naslov: Postano: 13:56 sub, 10. 4. 2010 Naslov: |
    |
|
|
@pmli Super, hvala, zbunjivala me ta dvostruka apsolutna vrijednost malo, a što se tiče drugog zadatka nisam znao pokazati da druga derivacija ima prekid u nuli, ali vidim da se to radi tako da se nađu dva niza koja konvergiraju različitim vrijednostima, tako da i nije neki problem.
@pmli Super, hvala, zbunjivala me ta dvostruka apsolutna vrijednost malo, a što se tiče drugog zadatka nisam znao pokazati da druga derivacija ima prekid u nuli, ali vidim da se to radi tako da se nađu dva niza koja konvergiraju različitim vrijednostima, tako da i nije neki problem.
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 14:44 ned, 11. 4. 2010 Naslov: Postano: 14:44 ned, 11. 4. 2010 Naslov: |
    |
|
|
Onda tako reci. :)
Dakle, [latex]f(x) = \begin{cases}
1-x^2, & x < 0 \\
a, & x = 0 \\
1+x, & x > 0
\end{cases}[/latex]. Vidimo da je [latex]a = 1[/latex], [latex]\lim_{x \to 0-} \frac{f(x) - f(0)}{x - 0} = 0[/latex] i [latex]\lim_{x \to 0+} \frac{f(x) - f(0)}{x - 0} = 1[/latex], što znači da je [latex]f[/latex] diferencijabilna svugdje osim u 0.
Onda tako reci. 
Dakle, 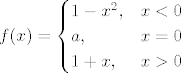 . Vidimo da je . Vidimo da je 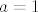 , , 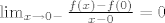 i i 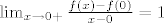 , što znači da je , što znači da je  diferencijabilna svugdje osim u 0. diferencijabilna svugdje osim u 0.
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
 Postano: 14:45 ned, 11. 4. 2010 Naslov: Postano: 14:45 ned, 11. 4. 2010 Naslov: |
    |
|
|
U kolokviju iz 2008.u zd 4.: f(x9=e^x/x
Ja dobivam da minimum f-je (1,e), ali da je točka (3/2,..) točka inleksije,kako je to moguće onda bi morala imati i max,šta ne?
U kolokviju iz 2008.u zd 4.: f(x9=e^x/x
Ja dobivam da minimum f-je (1,e), ali da je točka (3/2,..) točka inleksije,kako je to moguće onda bi morala imati i max,šta ne?
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
 Postano: 15:53 ned, 11. 4. 2010 Naslov: Postano: 15:53 ned, 11. 4. 2010 Naslov: |
    |
|
|
[quote="pmli"]Onda tako reci. :)
Dakle, [latex]f(x) = \begin{cases}
1-x^2, & x < 0 \\
a, & x = 0 \\
1+x, & x > 0
\end{cases}[/latex]. Vidimo da je [latex]a = 1[/latex], [latex]\lim_{x \to 0-} \frac{f(x) - f(0)}{x - 0} = 0[/latex] i [latex]\lim_{x \to 0+} \frac{f(x) - f(0)}{x - 0} = 1[/latex], što znači da je [latex]f[/latex] diferencijabilna svugdje osim u 0.[/quote]
hvala :D
| pmli (napisa): | Onda tako reci. 
Dakle, 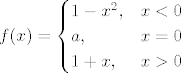 . Vidimo da je . Vidimo da je 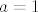 , , 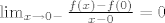 i i 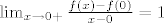 , što znači da je , što znači da je  diferencijabilna svugdje osim u 0. diferencijabilna svugdje osim u 0. |
hvala 
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
 Postano: 17:11 ned, 11. 4. 2010 Naslov: Postano: 17:11 ned, 11. 4. 2010 Naslov: |
    |
|
|
[quote="pmli"][url=http://www.wolframalpha.com/input/?i=Limit%281%2Fx^2-Sin%28x%29%2Fx^3%2Cx-%3E0%29]Može se dodefinirati.[/url] [size=6]Zašto nitko ne shvaća koliko je Mathematica MOĆNA?![/size][/quote]
krivo sam prepisala toga :oops:
ali sad ovaj treći iz treće grupe,ne ispada mi klase C1, i kad sam provjeravala rješenje wolframalphom ne ispiše, sigurno sam nešto pogriješila, možeš li mi ukazat gdje ,hvala
krivo sam prepisala toga 
ali sad ovaj treći iz treće grupe,ne ispada mi klase C1, i kad sam provjeravala rješenje wolframalphom ne ispiše, sigurno sam nešto pogriješila, možeš li mi ukazat gdje ,hvala
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|














