| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 15:52 pet, 9. 4. 2010 Naslov: Postano: 15:52 pet, 9. 4. 2010 Naslov: |
    |
|
|
Ova funkcija je ocito neprekidna na R osim (eventualno :D) u tocki 3.
Zato moramo odrediti gama (nek bude ubuduce y umjesto gama, lakse je pisat) t.d.[latex] lim_{x\rightarrow 3}f(x)=f(3)[/latex]
kad uvrstimo 3 u formulu od f, dobijemo [latex]f(3)= 1- e^{27-9y}[/latex]
Sad gledamo lijevi i desni limes funkcije u 3 (moraju bit jednaki)
lijevi limes=f(3), desni limes=ln(1)=0.
Iz toga zakljucujemo da mora biti f(3)=0 => y=3
Sad pogledamo derivabilnost (bitno je opet u x=3, ostalo znamo da je derivabilna)
Derivacija od ovog gornjeg dijela je 1/(x-2), od donjeg je [latex]-(3x^2-6x)e^{x^3-3x^2}
[/latex]
Sad vidimo da derivacija ima i lijevi i desni limes u tocki 3, ali oni su razliciti (1, odnosno -9 valjda) => znamo da derivacija ne moze imati prekid prve vrste, pa zakljucujemo da f nije dvb. u tocki x=3.
Za ekstreme samo treba provjerit tocke u kojima je f'(x)=0, rubne tocke (1 i 5) i ovu rupu u domeni derivacije (to jest 3)
Ova funkcija je ocito neprekidna na R osim (eventualno  ) u tocki 3. ) u tocki 3.
Zato moramo odrediti gama (nek bude ubuduce y umjesto gama, lakse je pisat) t.d.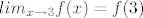
kad uvrstimo 3 u formulu od f, dobijemo 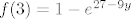
Sad gledamo lijevi i desni limes funkcije u 3 (moraju bit jednaki)
lijevi limes=f(3), desni limes=ln(1)=0.
Iz toga zakljucujemo da mora biti f(3)=0 ⇒ y=3
Sad pogledamo derivabilnost (bitno je opet u x=3, ostalo znamo da je derivabilna)
Derivacija od ovog gornjeg dijela je 1/(x-2), od donjeg je 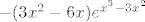
Sad vidimo da derivacija ima i lijevi i desni limes u tocki 3, ali oni su razliciti (1, odnosno -9 valjda) ⇒ znamo da derivacija ne moze imati prekid prve vrste, pa zakljucujemo da f nije dvb. u tocki x=3.
Za ekstreme samo treba provjerit tocke u kojima je f'(x)=0, rubne tocke (1 i 5) i ovu rupu u domeni derivacije (to jest 3)
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:52 pet, 9. 4. 2010 Naslov: Postano: 15:52 pet, 9. 4. 2010 Naslov: |
    |
|
|
Dakle, u a) i b) dijelu zadatka si utvrdio da je funkcija neprekidna i (vjerojatno, ako je imalo slično ostalim grupama :D) diferencijabilna svugdje osim u [latex]3[/latex].
Sad, znamo već otprije globalni ekstrem povezati s tim da je derivacija u točki jednaka nuli (Fermatova lema). Stoga, točke koje nas interesiraju su one u kojima derivacija postoji i jednaka je [latex]0[/latex] te one u kojima derivacija ne postoji (to je tu samo [latex]3[/latex]) - naravno, treba uključiti i rubove jer u Fermatovoj lemi moramo imati diferencijabilnost s obje strane točke.
Stoga, trebaš pogledati kad je [latex]f'(x)=0[/latex] ([latex]f'[/latex] ima jedan oblik prije trojke, a jedan poslije, pa bi i na to trebao paziti :P) te odrediti [latex]f(x)[/latex] za takve [latex]x[/latex]. Nakon toga, još pogledaj koliko je [latex]f(3)[/latex], [latex]f(1)[/latex] i [latex]f(5)[/latex]. Sada će globalni minimum biti najmanja vrijednost od svih koje si dobio, a globalni maksimum najveća.
Taj dio s gledanjem kad je derivacija 0 je čisti račun, tako da ću ga sad preskočiti, a ti reci ako ima problema. :) Čisto ovako naizgled mislim da je maksimum u [latex]5[/latex] ([latex]\ln 3[/latex]), a minimum u [latex]3[/latex] ([latex]0[/latex]), ali može biti da griješim.
Dakle, u a) i b) dijelu zadatka si utvrdio da je funkcija neprekidna i (vjerojatno, ako je imalo slično ostalim grupama  ) diferencijabilna svugdje osim u ) diferencijabilna svugdje osim u 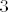 . .
Sad, znamo već otprije globalni ekstrem povezati s tim da je derivacija u točki jednaka nuli (Fermatova lema). Stoga, točke koje nas interesiraju su one u kojima derivacija postoji i jednaka je  te one u kojima derivacija ne postoji (to je tu samo te one u kojima derivacija ne postoji (to je tu samo 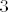 ) - naravno, treba uključiti i rubove jer u Fermatovoj lemi moramo imati diferencijabilnost s obje strane točke. ) - naravno, treba uključiti i rubove jer u Fermatovoj lemi moramo imati diferencijabilnost s obje strane točke.
Stoga, trebaš pogledati kad je 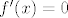 ( (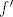 ima jedan oblik prije trojke, a jedan poslije, pa bi i na to trebao paziti ima jedan oblik prije trojke, a jedan poslije, pa bi i na to trebao paziti  ) te odrediti ) te odrediti 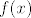 za takve za takve  . Nakon toga, još pogledaj koliko je . Nakon toga, još pogledaj koliko je 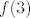 , , 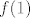 i i 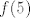 . Sada će globalni minimum biti najmanja vrijednost od svih koje si dobio, a globalni maksimum najveća. . Sada će globalni minimum biti najmanja vrijednost od svih koje si dobio, a globalni maksimum najveća.
Taj dio s gledanjem kad je derivacija 0 je čisti račun, tako da ću ga sad preskočiti, a ti reci ako ima problema.  Čisto ovako naizgled mislim da je maksimum u Čisto ovako naizgled mislim da je maksimum u  ( (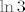 ), a minimum u ), a minimum u 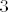 ( ( ), ali može biti da griješim. ), ali može biti da griješim.
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
bekse
Forumaš(ica)

Pridružen/a: 06. 11. 2009. (18:19:09)
Postovi: (19)16
|
|
| [Vrh] |
|
|






