Mislim da sam uspio u slučaju skupova konačne mjere, a zapravo me samo takvi i zanimaju.
Pokazat cu prvo da ako je [latex]B[/latex] [latex]\nu^\ast[/latex] izmjeriv i konačne mjere, da je tada i [latex]\mu^\ast (B) = \nu^\ast (B)[/latex]. Iz definicije vanjske mjere imam da za svaki [latex]\varepsilon > 0[/latex] postoje [latex]R_i \in \mathcal{S}_1[/latex] disjunktni (ako nisu napravim ih disjunktnima) td. [latex]R = \cup R_i \supseteq B[/latex] i [latex]\nu^\ast (B) + \varepsilon > \nu^\ast (R)[/latex]. Jer je B [latex]\nu^\ast[/latex] izmjeriv imamo [latex]\nu^\ast (R) = \nu^\ast (R \cap B) + \nu^\ast (R \setminus B)[/latex]. Iz toga je [latex]\mu^\ast (R \setminus B) \leq \nu^\ast (R \setminus B) < \varepsilon[/latex]. Tu se koristi konačnost od B da bi mogao oduzet [latex]\nu^\ast(B)[/latex] na obje strane. Iz [latex]\mu^\ast(B) + \mu^\ast(R \setminus B) \geq \mu^\ast(R)[/latex] je [latex]\varepsilon > \mu^\ast(R \setminus B) \geq \mu^\ast(R) - \mu^\ast (B)[/latex]. Pa iz [latex]\mu^\ast(B) + \varepsilon > \mu^\ast(R) = \nu^\ast(B)[/latex] imam da [latex]\mu^\ast(B) = \nu^\ast(B)[/latex].
Uf........
Sad jos da je [latex]B[/latex] [latex]\mu^\ast[/latex] izmjeriv.
Dovoljno je za [latex]A[/latex] konacne mjere vidjet da [latex]\mu^\ast(A) \geq \mu^\ast(A \cap B) + \mu^\ast(A \setminus B)[/latex]. Neka je [latex]R[/latex] kao i gore pokrivac od [latex]B[/latex] koji je [latex]\frac{\varepsilon}{2}[/latex]-dobar, a [latex]R_A[/latex] isto to za skup A. Sada je [latex]\mu^\ast(A) + \frac{\varepsilon}{2} > \mu^\ast(R_A)=\mu^\ast(R_A \cap R) + \mu^\ast(R_A \setminus R) \geq[/latex] [latex]\mu^\ast(A \cap B) + \mu^\ast(A \setminus R) \geq \mu^\ast(A \setminus B) - \frac{\varepsilon}{2} + \mu^\ast(A \cap B)[/latex], gdje poslijednja nejednakost slijedi iz [latex]A \setminus B = (A \setminus R) \cup ((R \setminus B) \cap A)[/latex]. Zbog proizvoljnosti [latex]\varepsilon[/latex] slijedi tvrdnja.
Eto, ako ce bit nesto (ili sve :D) krivo, valjda ce netko ispravit.
Mislim da sam uspio u slučaju skupova konačne mjere, a zapravo me samo takvi i zanimaju.
Pokazat cu prvo da ako je 
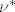 izmjeriv i konačne mjere, da je tada i
izmjeriv i konačne mjere, da je tada i 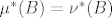 . Iz definicije vanjske mjere imam da za svaki
. Iz definicije vanjske mjere imam da za svaki  postoje
postoje 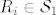 disjunktni (ako nisu napravim ih disjunktnima) td.
disjunktni (ako nisu napravim ih disjunktnima) td. 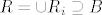 i
i 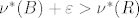 . Jer je B
. Jer je B 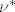 izmjeriv imamo
izmjeriv imamo 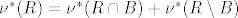 . Iz toga je
. Iz toga je 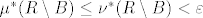 . Tu se koristi konačnost od B da bi mogao oduzet
. Tu se koristi konačnost od B da bi mogao oduzet 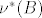 na obje strane. Iz
na obje strane. Iz 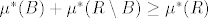 je
je 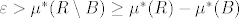 . Pa iz
. Pa iz 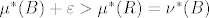 imam da
imam da 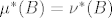 .
.
Uf........
Sad jos da je 
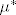 izmjeriv.
izmjeriv.
Dovoljno je za  konacne mjere vidjet da
konacne mjere vidjet da 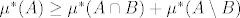 . Neka je
. Neka je 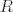 kao i gore pokrivac od
kao i gore pokrivac od  koji je
koji je 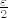 -dobar, a
-dobar, a 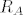 isto to za skup A. Sada je
isto to za skup A. Sada je 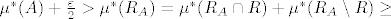
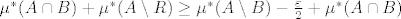 , gdje poslijednja nejednakost slijedi iz
, gdje poslijednja nejednakost slijedi iz 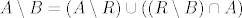 . Zbog proizvoljnosti
. Zbog proizvoljnosti  slijedi tvrdnja.
slijedi tvrdnja.
Eto, ako ce bit nesto (ili sve  ) krivo, valjda ce netko ispravit.
) krivo, valjda ce netko ispravit.
_________________
Jedan je smjer očit, a drugi je trivijalan.









