| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
athlet
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 18:14 ned, 30. 5. 2010 Naslov: Postano: 18:14 ned, 30. 5. 2010 Naslov: |
    |
|
|
Prva ideja koja mi pada na pamet je prilično brute force i u nekim koracima se dosta može optimizirati.
Ideja je ta da se formiraju sve uređene n-torke čiji su elementi iz skupa [-m,m]. To se postiže funkcijom [tt]Tuples[Range[-m,m],n][/tt]. Uređene n-torke će nam trebati jer će prva označavati slobodan član, druga koeficijent uz x, treća uz x^2 itd.
Sve te n-torke čine listu koju nazovemo npr. [tt]koef[/tt] i zatim pomoću funkcije [tt]FromCoefficientRules[/tt] konstruiramo sve polinome sa koeficijentima iz liste koef.
Funkcija [tt]FromCoefficientRules[/tt] zahtjeva poseban format pravila kojim konstruira polinome, a to pravilo je oblika
[code:1]{{0}->a[0],{1}->a[1],...,{n-1}->a[n-1]}[/code:1]
(vidi help za detalje) što znači da se 0-tom članu polinoma pridružuje koeficijent a[0], prvom članu se pridružuje koeficijent a[1] itd. pa će biti potrebno napisati funkciju koja uređenoj n-torki oblika {a[0],a[1],...,a[n-1]} pridružuje n-torku oblika {{0}->a[0],{1}->a[1],...,{n-1}->a[n-1]}. To nije teško, napravi se pomoću jedne for petlje i funkcije [tt]AppendTo[/tt].
Cijeli ovaj postupak se utrpa u funkciju koju nazovemo npr. [tt]generator[n_,m_][/tt] koja će vratiti listu sa svim generiranim polinomima.
To je bio najteži dio zadatka, dalje je jednostavnije. Za rješavanje polinoma mogu se koristiti funkcije [tt]Root[/tt] ili [tt]Solve[/tt], a prikaz u kompleksnoj ravnini je isto kao što i prikaz u [latex]\mathbb{R}^2[/latex] gdje je nultočka x+iy nekog polinoma prikazana kao točka (x,y) u [latex]\mathbb{R}^2[/latex].
[size=9][color=#999999]Added after 48 minutes:[/color][/size]
A evo i koda.
[quote][code:1]ToPolynomial[koef_List] := Module[{i, rules = {}},
For[i = 0, i <= Length[koef] - 1, i++,
AppendTo[rules, {i} -> koef[[i + 1]]]
];
Return[rules]
][/code:1]
[code:1]generator[n_Integer, m_Integer] :=
Module[{i, lista1 = {}, lista2 = {}, polinomi = {}},
lista1 = Tuples[Range[-m, m], n];
For[i = 1, i <= Length[lista1], i++,
AppendTo[lista2, ToPolynomial[lista1[[i]]]
];
];
polinomi = MapThread[FromCoefficientRules, {{lista2}, {x}}][[1]];
Return[polinomi]
][/code:1]
[code:1]Nul[poly_] := Module[{i, nultocke = {}},
For[i = 1, i <= Exponent[poly, x], i++,
AppendTo[nultocke, Root[poly, i]]];
Return[nultocke]
][/code:1]
[code:1]Koord[poly_] := Module[{lista = {}},
For[i = 1, i <= Length[Nul[poly]], i++,
AppendTo[lista, {Re[Nul[poly][[i]]], Im[Nul[poly][[i]]]}]
];
Return[lista]
][/code:1]
[code:1]NacrtajRjesenja[polinomi_List, element_Integer] :=
ListPlot[Koord[polinomi[[element]]]][/code:1]
Uz napomenu da su svi računi egzaktni. Budući postoje polinomi čije nultočke Mathematica ne zna egzaktno izračunati, za te polinome neće uspjeti nacrtati rješenja. Tu bi se trebala, kod traženja nultočaka polinoma u funkciji [tt]Nul[/tt], ubaciti neka funkcija koja će naći numeričko rješenje.
[/quote]
Prva ideja koja mi pada na pamet je prilično brute force i u nekim koracima se dosta može optimizirati.
Ideja je ta da se formiraju sve uređene n-torke čiji su elementi iz skupa [-m,m]. To se postiže funkcijom Tuples[Range[-m,m],n]. Uređene n-torke će nam trebati jer će prva označavati slobodan član, druga koeficijent uz x, treća uz x^2 itd.
Sve te n-torke čine listu koju nazovemo npr. koef i zatim pomoću funkcije FromCoefficientRules konstruiramo sve polinome sa koeficijentima iz liste koef.
Funkcija FromCoefficientRules zahtjeva poseban format pravila kojim konstruira polinome, a to pravilo je oblika
| Kod: | | {{0}->a[0],{1}->a[1],...,{n-1}->a[n-1]} |
(vidi help za detalje) što znači da se 0-tom članu polinoma pridružuje koeficijent a[0], prvom članu se pridružuje koeficijent a[1] itd. pa će biti potrebno napisati funkciju koja uređenoj n-torki oblika {a[0],a[1],...,a[n-1]} pridružuje n-torku oblika {{0}→a[0],{1}→a[1],...,{n-1}→a[n-1]}. To nije teško, napravi se pomoću jedne for petlje i funkcije AppendTo.
Cijeli ovaj postupak se utrpa u funkciju koju nazovemo npr. generator[n_,m_] koja će vratiti listu sa svim generiranim polinomima.
To je bio najteži dio zadatka, dalje je jednostavnije. Za rješavanje polinoma mogu se koristiti funkcije Root ili Solve, a prikaz u kompleksnoj ravnini je isto kao što i prikaz u 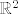 gdje je nultočka x+iy nekog polinoma prikazana kao točka (x,y) u gdje je nultočka x+iy nekog polinoma prikazana kao točka (x,y) u 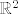 . .
Added after 48 minutes:
A evo i koda.
| Citat: | | Kod: | ToPolynomial[koef_List] := Module[{i, rules = {}},
For[i = 0, i <= Length[koef] - 1, i++,
AppendTo[rules, {i} -> koef[[i + 1]]]
];
Return[rules]
] |
| Kod: | generator[n_Integer, m_Integer] :=
Module[{i, lista1 = {}, lista2 = {}, polinomi = {}},
lista1 = Tuples[Range[-m, m], n];
For[i = 1, i <= Length[lista1], i++,
AppendTo[lista2, ToPolynomial[lista1[[i]]]
];
];
polinomi = MapThread[FromCoefficientRules, {{lista2}, {x}}][[1]];
Return[polinomi]
] |
| Kod: | Nul[poly_] := Module[{i, nultocke = {}},
For[i = 1, i <= Exponent[poly, x], i++,
AppendTo[nultocke, Root[poly, i]]];
Return[nultocke]
] |
| Kod: | Koord[poly_] := Module[{lista = {}},
For[i = 1, i <= Length[Nul[poly]], i++,
AppendTo[lista, {Re[Nul[poly][[i]]], Im[Nul[poly][[i]]]}]
];
Return[lista]
] |
| Kod: | NacrtajRjesenja[polinomi_List, element_Integer] :=
ListPlot[Koord[polinomi[[element]]]] |
Uz napomenu da su svi računi egzaktni. Budući postoje polinomi čije nultočke Mathematica ne zna egzaktno izračunati, za te polinome neće uspjeti nacrtati rješenja. Tu bi se trebala, kod traženja nultočaka polinoma u funkciji Nul, ubaciti neka funkcija koja će naći numeričko rješenje.
|
_________________
The Dude Abides
Zadnja promjena: goranm; 20:54 ned, 30. 5. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Gost
|
 Postano: 18:48 ned, 30. 5. 2010 Naslov: Postano: 18:48 ned, 30. 5. 2010 Naslov: |
    |
|
|
Stvarno se zahvaljujem na iscrpnom odgovoru. Vidim da si mi napisao i kod, pošto ja nisam baš upućen skroz u mathematicu ipak su mi neke stvarni ne jasne. Ovo kod rules mi nije jasno šta se tu ustvari definira. Ako mi možeš malo pojasnit kod
[code:1]{{0}->a[0],{1}->a[1],...,{n-1}->a[n-1]}[/code:1]
kako da definiram te sve članove, jer mi , ..., ne prihvaća te točkice?
Stvarno se zahvaljujem na iscrpnom odgovoru. Vidim da si mi napisao i kod, pošto ja nisam baš upućen skroz u mathematicu ipak su mi neke stvarni ne jasne. Ovo kod rules mi nije jasno šta se tu ustvari definira. Ako mi možeš malo pojasnit kod
| Kod: | | {{0}->a[0],{1}->a[1],...,{n-1}->a[n-1]} |
kako da definiram te sve članove, jer mi , ..., ne prihvaća te točkice?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:52 ned, 30. 5. 2010 Naslov: Postano: 20:52 ned, 30. 5. 2010 Naslov: |
    |
|
|
To su pravila pomoću kojih mathematica generira polinom kada su zadani samo koeficijenti.
Npr. sa
[code:1]FromCoefficientRules[{{0}->1,{1}->1,{2}->1,{3}->1},x][/code:1]
generirati će se polinom [latex]1+x+x^2+x^3[/latex], dok će
[code:1]FromCoefficientRules[{{0}->-17,{1}->3,{2}->7,{3}->-5,{4}->9},x][/code:1]
generirati polinom [latex]-17+3x+7x^2-5x^3+9x^4[/latex].
Točkice neće prihvatiti jer eksplicitno moraš definirati sve koeficijente. Ukoliko želiš generirati polinom npr. [latex]17+19x^3[/latex] moraš pozvati funkciju [tt]FromCoefficientRules[/tt] sa argumentom
[code:1]{{0}->17,{1}->0,{2}->0,{3}->19}[/code:1]
To su pravila pomoću kojih mathematica generira polinom kada su zadani samo koeficijenti.
Npr. sa
| Kod: | | FromCoefficientRules[{{0}->1,{1}->1,{2}->1,{3}->1},x] |
generirati će se polinom 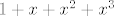 , dok će , dok će
| Kod: | | FromCoefficientRules[{{0}->-17,{1}->3,{2}->7,{3}->-5,{4}->9},x] |
generirati polinom 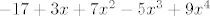 . .
Točkice neće prihvatiti jer eksplicitno moraš definirati sve koeficijente. Ukoliko želiš generirati polinom npr.  moraš pozvati funkciju FromCoefficientRules sa argumentom moraš pozvati funkciju FromCoefficientRules sa argumentom
| Kod: | | {{0}->17,{1}->0,{2}->0,{3}->19} |
_________________
The Dude Abides
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 14:59 pon, 31. 5. 2010 Naslov: Postano: 14:59 pon, 31. 5. 2010 Naslov: |
    |
|
|
[quote="Anonymous"][quote="goranm"]Da, moj kod radi. Ne mogu ti bolje pomoći ako ne napišeš svoj kod i što se izbaci kao output, neka greška ili nešto drugo.[/quote]
Kad ga probam u Mathematici ništa mi ne izbacuje, pa sam mislio možda da nisi sve varijable definirao, nemam pojma. Pretpostavljam da ja nešto krivo radim samo ni nije jasno šta.[/quote]
Napiši ovdje točno ono što si napisao u Mathematici (ili napravi printscreen presliku ekrana), ovako napamet ne mogu znati zašto ti ne radi.
| Anonymous (napisa): | | goranm (napisa): | | Da, moj kod radi. Ne mogu ti bolje pomoći ako ne napišeš svoj kod i što se izbaci kao output, neka greška ili nešto drugo. |
Kad ga probam u Mathematici ništa mi ne izbacuje, pa sam mislio možda da nisi sve varijable definirao, nemam pojma. Pretpostavljam da ja nešto krivo radim samo ni nije jasno šta. |
Napiši ovdje točno ono što si napisao u Mathematici (ili napravi printscreen presliku ekrana), ovako napamet ne mogu znati zašto ti ne radi.
_________________
The Dude Abides
|
|
| [Vrh] |
|
Gost
|
 Postano: 15:39 pon, 31. 5. 2010 Naslov: Postano: 15:39 pon, 31. 5. 2010 Naslov: |
    |
|
|
[code:1]ToPolynomial[koef_List] := Module[{i, rules = {}},
For[i = 0, i <= Length[koef] - 1, i++,
AppendTo[rules, {i} -> koef[[i + 1]]]
];
Return[rules]
]
generator[n_Integer, m_Integer] :=
Module[{i, lista1 = {}, lista2 = {}, polinomi = {}},
lista1 = Tuples[Range[-m, m], n];
For[i = 1, i <= Length[lista1], i++,
AppendTo[lista2, ToPolynomial[lista1[[i]]]
];
];
polinomi = MapThread[FromCoefficientRules, {{lista2}, {x}}][[1] ];
Return[polinomi]
]
Nul[poly_] := Module[{i, nultocke = {}},
For[i = 1, i <= Exponent[poly, x], i++,
AppendTo[nultocke, Root[poly, i]]];
Return[nultocke]
]
Koord[poly_] := Module[{lista = {}},
For[i = 1, i <= Length[Nul[poly]], i++,
AppendTo[lista, {Re[Nul[poly][[i]]], Im[Nul[poly][[i]]]}]
];
Return[lista]
]
NacrtajRjesenja[polinomi_List, element_Integer] :=
ListPlot[Koord[polinomi[[element]]]][/code:1]
Ubacim kao što si i ti napisao prvi put kod. Kad ga pokušam pokrenuti ništa se ne događa. Nešto krivo radim, a neznam što.
| Kod: | ToPolynomial[koef_List] := Module[{i, rules = {}},
For[i = 0, i <= Length[koef] - 1, i++,
AppendTo[rules, {i} -> koef[[i + 1]]]
];
Return[rules]
]
generator[n_Integer, m_Integer] :=
Module[{i, lista1 = {}, lista2 = {}, polinomi = {}},
lista1 = Tuples[Range[-m, m], n];
For[i = 1, i <= Length[lista1], i++,
AppendTo[lista2, ToPolynomial[lista1[[i]]]
];
];
polinomi = MapThread[FromCoefficientRules, {{lista2}, {x}}][[1] ];
Return[polinomi]
]
Nul[poly_] := Module[{i, nultocke = {}},
For[i = 1, i <= Exponent[poly, x], i++,
AppendTo[nultocke, Root[poly, i]]];
Return[nultocke]
]
Koord[poly_] := Module[{lista = {}},
For[i = 1, i <= Length[Nul[poly]], i++,
AppendTo[lista, {Re[Nul[poly][[i]]], Im[Nul[poly][[i]]]}]
];
Return[lista]
]
NacrtajRjesenja[polinomi_List, element_Integer] :=
ListPlot[Koord[polinomi[[element]]]] |
Ubacim kao što si i ti napisao prvi put kod. Kad ga pokušam pokrenuti ništa se ne događa. Nešto krivo radim, a neznam što.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 15:53 pon, 31. 5. 2010 Naslov: Postano: 15:53 pon, 31. 5. 2010 Naslov: |
    |
|
|
Ništa se ne događa jer se te funkcije, nakon učitavanja, trebaju i pokrenut sa nekim konkretnim argumentima.
Nakon što te funkcije učitaš u memoriju i onda upišeš npr. [tt]generator[3,2][/tt], to će generirati sve polinome stupnja manjeg od 3 sa cjelobrojnim koeficijentima iz [-2,2], tj. napraviti će se lista čiji su elementi takvi polinomi.
Funkcijom [tt]NacrtajRjesenja[generator[n,m],i][/tt] nacrtati će rješenja i-tog polinoma u listi [tt]generator[n,m][/tt].
Npr. [tt]NacrtajRjesenja[generator[3,2],1][/tt] nacrtati će rješenja polinoma -2-2x-2x^2 jer je taj polinom prvi element liste [tt]generator[3,2][/tt].
Samo mala napomena: jer su svi računi egzaktni, Mathematica neće moći egzaktno naći rješenja nekih polinoma i tu bi se funkcije za nalaženje nultočaka trebale zamijeniti pripadnim numeričkim funkcijama.
Ništa se ne događa jer se te funkcije, nakon učitavanja, trebaju i pokrenut sa nekim konkretnim argumentima.
Nakon što te funkcije učitaš u memoriju i onda upišeš npr. generator[3,2], to će generirati sve polinome stupnja manjeg od 3 sa cjelobrojnim koeficijentima iz [-2,2], tj. napraviti će se lista čiji su elementi takvi polinomi.
Funkcijom NacrtajRjesenja[generator[n,m],i] nacrtati će rješenja i-tog polinoma u listi generator[n,m].
Npr. NacrtajRjesenja[generator[3,2],1] nacrtati će rješenja polinoma -2-2x-2x^2 jer je taj polinom prvi element liste generator[3,2].
Samo mala napomena: jer su svi računi egzaktni, Mathematica neće moći egzaktno naći rješenja nekih polinoma i tu bi se funkcije za nalaženje nultočaka trebale zamijeniti pripadnim numeričkim funkcijama.
_________________
The Dude Abides
|
|
| [Vrh] |
|
Gost
|
 Postano: 16:05 pon, 31. 5. 2010 Naslov: Postano: 16:05 pon, 31. 5. 2010 Naslov: |
    |
|
|
In[41]:= generator[3, 2]
During evaluation of In[41]:= FromCoefficientRules::cstruct: The coefficient list {ToPolynomial[Range[-m,m]],ToPolynomial[n]} does not have the correct structure. >>
Out[41]= FromCoefficientRules[{ToPolynomial[Range[-m, m]],
ToPolynomial[n]}, x][code]
To dobijem sad, kad unesem generator[3,2].
In[41]:= generator[3, 2]
During evaluation of In[41]:= FromCoefficientRules::cstruct: The coefficient list {ToPolynomial[Range[-m,m]],ToPolynomial[n]} does not have the correct structure. >>
Out[41]= FromCoefficientRules[{ToPolynomial[Range[-m, m]],
ToPolynomial[n]}, x][code]
To dobijem sad, kad unesem generator[3,2].
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 18:12 pon, 31. 5. 2010 Naslov: Postano: 18:12 pon, 31. 5. 2010 Naslov: |
    |
|
|
Kužim sad kako radi i sve, ali tek kad si mi objasnio. Da dobijem sva rješenja, znači brojčana, trebao bi koristit funkciju NSolve. Komplicirano mi je to napravit za svaki, odnosno u petlji jer nisam skoro pa nikad radio u mathematici. Jesam neke trivijalne zadatke, ali ovo je ipak puno kompliciranije. Isto tako bi mi trebao sve te točke nacrtati na jednom grafu.
Kužim sad kako radi i sve, ali tek kad si mi objasnio. Da dobijem sva rješenja, znači brojčana, trebao bi koristit funkciju NSolve. Komplicirano mi je to napravit za svaki, odnosno u petlji jer nisam skoro pa nikad radio u mathematici. Jesam neke trivijalne zadatke, ali ovo je ipak puno kompliciranije. Isto tako bi mi trebao sve te točke nacrtati na jednom grafu.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 18:48 pon, 31. 5. 2010 Naslov: Postano: 18:48 pon, 31. 5. 2010 Naslov: |
    |
|
|
Da, možeš sa for petljom u kojoj [tt]i[/tt] ide od 1 do [tt]Length[generator[n,m]][/tt] i u svakom koraku računa nultočkue od [tt]generator[n,m][[i]][/tt], tj. od i-tog polinoma u listi generator[n,m]. Rješenja polinoma nalaze se funkcijom [tt]Roots[/tt] ili [tt]Solve[/tt].
Malo brži (i puno manje čitljiv) način je da funkciju [tt]Roots[/tt] primijeniš na čitavu listu generator[n,m], npr.
[code:1]Map[Roots[#, x] &, Map[# == 0 &, generator[3, 2]]][/code:1]
će izbaciti rješenja za sve polinome (osim konstantnih) u listi generator[3,2].
Ako trebaš rješenja svih polinoma nacrtat na jednom grafu, onda se samo treba formirati lista čiji su elementi koordinate (x,y) koje predstavljaju nultočku x+iy nekog polinoma. Funkciju koja nultočke x+iy nekog polinoma pretvara u koordinate (x,y) već imaš, to je funkcija [tt]Koord[poly][/tt]. Sada se samo treba nekako formirati lista svih nultočaka, npr. sa
[code:1]SveNultocke[polinomi_List] := Module[{i, nultocke = {}},
nultocke = Koord[polinomi[[1]]];
For[i = 2, i <= Length[polinomi], i++,
nultocke = Union[nultocke, Koord[polinomi[[i]]]]
];
Return[nultocke]
][/code:1]
i onda će se pozivom funkcije
[code:1]ListPlot[SveNultocke[generator[3,2]]][/code:1] nacrtati sve nultocke svih polinoma stupnja manjeg od 3 sa cjelobrojnim koeficijentima iz [-2,2].
Da, možeš sa for petljom u kojoj i ide od 1 do Length[generator[n,m]] i u svakom koraku računa nultočkue od generator[n,m][[i]], tj. od i-tog polinoma u listi generator[n,m]. Rješenja polinoma nalaze se funkcijom Roots ili Solve.
Malo brži (i puno manje čitljiv) način je da funkciju Roots primijeniš na čitavu listu generator[n,m], npr.
| Kod: | | Map[Roots[#, x] &, Map[# == 0 &, generator[3, 2]]] |
će izbaciti rješenja za sve polinome (osim konstantnih) u listi generator[3,2].
Ako trebaš rješenja svih polinoma nacrtat na jednom grafu, onda se samo treba formirati lista čiji su elementi koordinate (x,y) koje predstavljaju nultočku x+iy nekog polinoma. Funkciju koja nultočke x+iy nekog polinoma pretvara u koordinate (x,y) već imaš, to je funkcija Koord[poly]. Sada se samo treba nekako formirati lista svih nultočaka, npr. sa
| Kod: | SveNultocke[polinomi_List] := Module[{i, nultocke = {}},
nultocke = Koord[polinomi[[1]]];
For[i = 2, i <= Length[polinomi], i++,
nultocke = Union[nultocke, Koord[polinomi[[i]]]]
];
Return[nultocke]
] |
i onda će se pozivom funkcije
| Kod: | | ListPlot[SveNultocke[generator[3,2]]] |
nacrtati sve nultocke svih polinoma stupnja manjeg od 3 sa cjelobrojnim koeficijentima iz [-2,2].
_________________
The Dude Abides
|
|
| [Vrh] |
|
|










