| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
spot137
Forumaš(ica)
Pridružen/a: 02. 11. 2009. (13:33:18)
Postovi: (55)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
 Postano: 14:30 ned, 20. 6. 2010 Naslov: Postano: 14:30 ned, 20. 6. 2010 Naslov: |
    |
|
|
[quote="meda"]
i još jedno pitanje..npr. 2. zad iz popravnog 2008. tre odredit intervale konveksnosti i konkavnosti i bla bla...
f(x)=x/(ln(x)) i sad pošto je domena <1,+beskonačno> jel tablicu radim za <1,+beskonačno> il ne? znam da inače gledam točke koje nisu u domeni funkcije al tu su mi i 1. i 2. derivacija nešto kroz lnx na nešto...?? nisam baš najbolje postavila pitanje, al nadam se da je barem djelomično jasno[/quote]
Domena je: <0, 1>U<1, +00>. U tablicu upisuješ 0, 1, e^2 (nultočka f'') i +beskonačno. Funkcija je konkavna na <0, 1> i <e^2, +00> a konveksna na <1, e^2> i točka infleksije je (e^2, e^2/2).
| meda (napisa): |
i još jedno pitanje..npr. 2. zad iz popravnog 2008. tre odredit intervale konveksnosti i konkavnosti i bla bla...
f(x)=x/(ln(x)) i sad pošto je domena <1,+beskonačno> jel tablicu radim za <1,+beskonačno> il ne? znam da inače gledam točke koje nisu u domeni funkcije al tu su mi i 1. i 2. derivacija nešto kroz lnx na nešto...?? nisam baš najbolje postavila pitanje, al nadam se da je barem djelomično jasno |
Domena je: <0, 1>U<1, +00>. U tablicu upisuješ 0, 1, e^2 (nultočka f'') i +beskonačno. Funkcija je konkavna na <0, 1> i <e^2, +00> a konveksna na <1, e^2> i točka infleksije je (e^2, e^2/2).
|
|
| [Vrh] |
|
crazy
Forumaš(ica)

Pridružen/a: 13. 06. 2010. (19:06:23)
Postovi: (16)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
crazy
Forumaš(ica)

Pridružen/a: 13. 06. 2010. (19:06:23)
Postovi: (16)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
crazy
Forumaš(ica)

Pridružen/a: 13. 06. 2010. (19:06:23)
Postovi: (16)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 15:22 ned, 20. 6. 2010 Naslov: Postano: 15:22 ned, 20. 6. 2010 Naslov: |
    |
|
|
[quote="eve"][quote="pmli"][quote="eve"]Odredite radijus konvergencije :
2^(n^2)*x^(n!)[/quote]
[url=http://degiorgi.math.hr/forum/viewtopic.php?t=15073&start=80]Ovdje[/url][/quote]
ne razumijem to..Muci me to sto je na x-u n!
Jel bi mogo objasnit to malo, fakat mi nije jasno.. Kak da izracunam R kad na x-u imam nesto sto nije n?[/quote]
Jesi li vidjela ova dva posta:
[quote="pmli"][latex]a_n = \left\{
\begin{array}{cll}
2^{n^2} \!\!\!\!\! & , & (\exists \, k \in \mathbb{N}) \, n = k! \\
0 \!\!\!\!\! & , & (\forall \, k \in \mathbb{N}) \, n \neq k!
\end{array} \right.[/latex][/quote]
[quote="pbakic"]idemo recimo zapisat red kao [latex]\sum a_n x^n[/latex]
Sad je ocito ovo sto je pmli napisao, znaci vecina ovih je 0
Tocnije, kad ti dodjes do potencije x^n!, imat ces [latex]\displaystyle a_{n!} = 2^{n^2}[/latex]. Dakle ovaj koeficijent je tek n!-ti po redu, pa zato ne vadimo obicni n-ti korijen nego n!-ti korijen. Dobije se [latex]\displaystyle \limsup_{n \to +\infty} \sqrt[n]{a_n} = \lim_{n \to +\infty} \sqrt[n!]{a_{n!}} = 2^0 = 1[/latex][/quote]
| eve (napisa): | | pmli (napisa): | | eve (napisa): | Odredite radijus konvergencije :
2^(n^2)*x^(n!) |
Ovdje |
ne razumijem to..Muci me to sto je na x-u n!
Jel bi mogo objasnit to malo, fakat mi nije jasno.. Kak da izracunam R kad na x-u imam nesto sto nije n? |
Jesi li vidjela ova dva posta:
| pmli (napisa): | 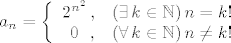 |
| pbakic (napisa): | idemo recimo zapisat red kao 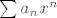
Sad je ocito ovo sto je pmli napisao, znaci vecina ovih je 0
Tocnije, kad ti dodjes do potencije x^n!, imat ces  . Dakle ovaj koeficijent je tek n!-ti po redu, pa zato ne vadimo obicni n-ti korijen nego n!-ti korijen. Dobije se . Dakle ovaj koeficijent je tek n!-ti po redu, pa zato ne vadimo obicni n-ti korijen nego n!-ti korijen. Dobije se 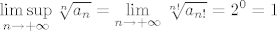 |
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
 Postano: 16:14 ned, 20. 6. 2010 Naslov: Postano: 16:14 ned, 20. 6. 2010 Naslov: |
    |
|
|
@pmli
vidjela sam ta dva post, ali ne kuzim bas :oops:
da li to znaci da svaki put kad na x-u imam nesto sto nije n vadim taj neki,a ne n-ti korjen?
I,jos jedno pitanje, sta ako imam zadatak da je zgodno to rjesit preko D'Alemberta, da li normalno gledam an+1/an ali kak(ako je na x-u nesto drugo osimn)?
@pmli
vidjela sam ta dva post, ali ne kuzim bas 
da li to znaci da svaki put kad na x-u imam nesto sto nije n vadim taj neki,a ne n-ti korjen?
I,jos jedno pitanje, sta ako imam zadatak da je zgodno to rjesit preko D'Alemberta, da li normalno gledam an+1/an ali kak(ako je na x-u nesto drugo osimn)?
Zadnja promjena: eve; 16:40 ned, 20. 6. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
spot137
Forumaš(ica)
Pridružen/a: 02. 11. 2009. (13:33:18)
Postovi: (55)16
Spol: 
|
|
| [Vrh] |
|
crazy
Forumaš(ica)

Pridružen/a: 13. 06. 2010. (19:06:23)
Postovi: (16)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 16:44 ned, 20. 6. 2010 Naslov: Postano: 16:44 ned, 20. 6. 2010 Naslov: |
    |
|
|
@niveus: [latex]\displaystyle \sqrt{n^2 + n} - \sqrt{n} = \frac{n^2 + n - n}{\sqrt{n^2 + n} + \sqrt{n}} = \frac{n^2}{\sqrt{n^2 + n} + \sqrt{n}}[/latex] Pomaže li to?
@eve: Da, jer se u priči javlja [latex]\displaystyle \sqrt[n]{|a_n|}[/latex], što znači da se korijen i indeks moraju poklopiti (primjeti: [latex]\sum a_n x^n[/latex], ne [latex]\sum a_n x^{n!}[/latex]).
Što se tiče D'Alamberta, teško će to ići, jer će za dosta [latex]n \in \mathbb{N}[/latex] vrijediti [latex]a_n = 0[/latex].
@niveus: 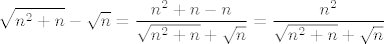 Pomaže li to? Pomaže li to?
@eve: Da, jer se u priči javlja 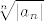 , što znači da se korijen i indeks moraju poklopiti (primjeti: , što znači da se korijen i indeks moraju poklopiti (primjeti: 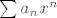 , ne , ne 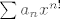 ). ).
Što se tiče D'Alamberta, teško će to ići, jer će za dosta  vrijediti vrijediti 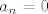 . .
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
crazy
Forumaš(ica)

Pridružen/a: 13. 06. 2010. (19:06:23)
Postovi: (16)16
|
|
| [Vrh] |
|
|
















