| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:04 sri, 6. 10. 2010 Naslov: Postano: 19:04 sri, 6. 10. 2010 Naslov: |
    |
|
|
Uz rizik da zvučim grub, sigurno da ima ekipe koja zna riješiti zadaću. Kad razmisliš, ima i ekipe koja zna riješiti kolokvije, ima i ekipe koja ih štoviše sastavlja... ispostavlja se da zapravo za dosta stvari na svijetu ima ekipe koja to zna riješiti. :P Ali to nije poanta, nego da sam probaš. Stoga, ajd' probaj riješiti to što te zanima, pa pitaj gdje zapneš (ili za hint u vezi nekog zadatka, to nije problem dati... ili ako hoćeš provjeriti rješenje). :) Onda će, jamčim, biti ekipe koja će ti pomoći. :) (Znam da nisi loše mislio, a zadaci pri kraju zbilja mi se ne čine prelagani, ali kvragu, kako odgovoriti čovjeku koji eksplicitno traži da mu se daju gotova rješenja domaće zadaće. :P)
Inače, nisam 100% siguran kakva su pravila ove godine, ali zadnjih par godina nije trebalo riješiti sve zadatke u zadaći - trebalo je riješiti četiri ili možda pet zadataka. Sad, ne znam, možda se nešto promijenilo, ali, koliko vidim, zadaće i dalje nose 10 bodova, pa bi barem meni bilo razumno očekivati da i dalje vrijede otprilike ista pravila (tj. da se ne mora riješiti sve). Vjerojatno su vam asistenti natuknuli nešto o tome na vježbama (na kojima ste svi jamačno bili :D)... vidim da na webu nema ničega. :? Ali kažem, možda i griješim.
Uz rizik da zvučim grub, sigurno da ima ekipe koja zna riješiti zadaću. Kad razmisliš, ima i ekipe koja zna riješiti kolokvije, ima i ekipe koja ih štoviše sastavlja... ispostavlja se da zapravo za dosta stvari na svijetu ima ekipe koja to zna riješiti.  Ali to nije poanta, nego da sam probaš. Stoga, ajd' probaj riješiti to što te zanima, pa pitaj gdje zapneš (ili za hint u vezi nekog zadatka, to nije problem dati... ili ako hoćeš provjeriti rješenje). Ali to nije poanta, nego da sam probaš. Stoga, ajd' probaj riješiti to što te zanima, pa pitaj gdje zapneš (ili za hint u vezi nekog zadatka, to nije problem dati... ili ako hoćeš provjeriti rješenje).  Onda će, jamčim, biti ekipe koja će ti pomoći. Onda će, jamčim, biti ekipe koja će ti pomoći.  (Znam da nisi loše mislio, a zadaci pri kraju zbilja mi se ne čine prelagani, ali kvragu, kako odgovoriti čovjeku koji eksplicitno traži da mu se daju gotova rješenja domaće zadaće. (Znam da nisi loše mislio, a zadaci pri kraju zbilja mi se ne čine prelagani, ali kvragu, kako odgovoriti čovjeku koji eksplicitno traži da mu se daju gotova rješenja domaće zadaće.  ) )
Inače, nisam 100% siguran kakva su pravila ove godine, ali zadnjih par godina nije trebalo riješiti sve zadatke u zadaći - trebalo je riješiti četiri ili možda pet zadataka. Sad, ne znam, možda se nešto promijenilo, ali, koliko vidim, zadaće i dalje nose 10 bodova, pa bi barem meni bilo razumno očekivati da i dalje vrijede otprilike ista pravila (tj. da se ne mora riješiti sve). Vjerojatno su vam asistenti natuknuli nešto o tome na vježbama (na kojima ste svi jamačno bili  )... vidim da na webu nema ničega. )... vidim da na webu nema ničega.  Ali kažem, možda i griješim. Ali kažem, možda i griješim.
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 19:54 sri, 6. 10. 2010 Naslov: Postano: 19:54 sri, 6. 10. 2010 Naslov: |
    |
|
|
probo ja ,rijesio ja neke(dosta njih) al ima kompliciranijih koje tipa ,ja bi reko jos nismo ni obradili,pa me zanima ako ima tko ko je rijesio takve pa da kaze kako ih je rijesio...
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
[quote="mornik"]Uz rizik da zvučim grub, sigurno da ima ekipe koja zna riješiti zadaću. Kad razmisliš, ima i ekipe koja zna riješiti kolokvije, ima i ekipe koja ih štoviše sastavlja... ispostavlja se da zapravo za dosta stvari na svijetu ima ekipe koja to zna riješiti. :P Ali to nije poanta, nego da sam probaš. Stoga, ajd' probaj riješiti to što te zanima, pa pitaj gdje zapneš (ili za hint u vezi nekog zadatka, to nije problem dati... ili ako hoćeš provjeriti rješenje). :) Onda će, jamčim, biti ekipe koja će ti pomoći. :) (Znam da nisi loše mislio, a zadaci pri kraju zbilja mi se ne čine prelagani, ali kvragu, kako odgovoriti čovjeku koji eksplicitno traži da mu se daju gotova rješenja domaće zadaće. :P)
Inače, nisam 100% siguran kakva su pravila ove godine, ali zadnjih par godina nije trebalo riješiti sve zadatke u zadaći - trebalo je riješiti četiri ili možda pet zadataka. Sad, ne znam, možda se nešto promijenilo, ali, koliko vidim, zadaće i dalje nose 10 bodova, pa bi barem meni bilo razumno očekivati da i dalje vrijede otprilike ista pravila (tj. da se ne mora riješiti sve). Vjerojatno su vam asistenti natuknuli nešto o tome na vježbama (na kojima ste svi jamačno bili :D)... vidim da na webu nema ničega. :? Ali kažem, možda i griješim.[/quote]
ove godine mislim da je reko asistent,ako se ne varam da moramo rijesiti pola zadace a ako ima 33 zadatka,to je onda 17 ih moramo rijesiti...
probo ja ,rijesio ja neke(dosta njih) al ima kompliciranijih koje tipa ,ja bi reko jos nismo ni obradili,pa me zanima ako ima tko ko je rijesio takve pa da kaze kako ih je rijesio...
Added after 2 minutes:
| mornik (napisa): | Uz rizik da zvučim grub, sigurno da ima ekipe koja zna riješiti zadaću. Kad razmisliš, ima i ekipe koja zna riješiti kolokvije, ima i ekipe koja ih štoviše sastavlja... ispostavlja se da zapravo za dosta stvari na svijetu ima ekipe koja to zna riješiti.  Ali to nije poanta, nego da sam probaš. Stoga, ajd' probaj riješiti to što te zanima, pa pitaj gdje zapneš (ili za hint u vezi nekog zadatka, to nije problem dati... ili ako hoćeš provjeriti rješenje). Ali to nije poanta, nego da sam probaš. Stoga, ajd' probaj riješiti to što te zanima, pa pitaj gdje zapneš (ili za hint u vezi nekog zadatka, to nije problem dati... ili ako hoćeš provjeriti rješenje).  Onda će, jamčim, biti ekipe koja će ti pomoći. Onda će, jamčim, biti ekipe koja će ti pomoći.  (Znam da nisi loše mislio, a zadaci pri kraju zbilja mi se ne čine prelagani, ali kvragu, kako odgovoriti čovjeku koji eksplicitno traži da mu se daju gotova rješenja domaće zadaće. (Znam da nisi loše mislio, a zadaci pri kraju zbilja mi se ne čine prelagani, ali kvragu, kako odgovoriti čovjeku koji eksplicitno traži da mu se daju gotova rješenja domaće zadaće.  ) )
Inače, nisam 100% siguran kakva su pravila ove godine, ali zadnjih par godina nije trebalo riješiti sve zadatke u zadaći - trebalo je riješiti četiri ili možda pet zadataka. Sad, ne znam, možda se nešto promijenilo, ali, koliko vidim, zadaće i dalje nose 10 bodova, pa bi barem meni bilo razumno očekivati da i dalje vrijede otprilike ista pravila (tj. da se ne mora riješiti sve). Vjerojatno su vam asistenti natuknuli nešto o tome na vježbama (na kojima ste svi jamačno bili  )... vidim da na webu nema ničega. )... vidim da na webu nema ničega.  Ali kažem, možda i griješim. Ali kažem, možda i griješim. |
ove godine mislim da je reko asistent,ako se ne varam da moramo rijesiti pola zadace a ako ima 33 zadatka,to je onda 17 ih moramo rijesiti...
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 9:50 pet, 8. 10. 2010 Naslov: Postano: 9:50 pet, 8. 10. 2010 Naslov: |
    |
|
|
Da, obično na kraju zadaće budu teži zadaci koji baš i nisu potpuno obrađeni gradivom na nastavi. Zato (according to Lepi) i možete izabrati pet zadataka i predati ih. :)
Koliko vidim, neki (većina?) zadataka tu se mogu riješiti s [url=http://en.wikipedia.org/wiki/Generalized_mean]nejednakostima sredina[/url] (u 18., su u pitanju, čini mi se, A-H i A-G, a nisam vidio da se negdje spominju nejednakosti sredina u svom općenitom obliku). Neki dokazi vjerojatno mogu i indukcijom, makar mi se ne čini baš trivijalno. E, da, čisto ako ćete rješavati, ako se ne varam, vidio sam tipfelere u 18. zadatku (naravno, u nazivniku prve nejednakosti je [latex]a+b+c[/latex]) i 24. zadatku (sve vrijedi, samo se [latex]H_n[/latex] zove harmonijska, a ne kvadratna sredina).
Uglavnom, neki zadaci će biti poznati ljudima koji su se pripremali za natjecanja u srednjoj školi (Cauchy-Schwarz-Bunyakovsky, K-A-G-H itd.). Ako vas zanima, našao sam [url=http://www.artofproblemsolving.com/Resources/Papers/MildorfInequalities.pdf]par[/url] [url=http://web.mit.edu/rwbarton/Public/mop/famous-inequalities.pdf]linkova[/url] gdje možete vidjeti neke poznate nejednakosti (s tim da se tamo obrađuje puno veći broj poznatih i relativno teških nejednakosti, tu u zadaći vjerojatno ne treba velika većina toga). Kao što rekoh, ta je tema dosta popularna na raznim natjecanjima iz matematike (pogotovo na višim razinama pa sve do međunarodnih tipa IMO i sl.), tako da ima dosta razumljivih stvari po Internetu. :)
S tim da se nemojte uplašiti - dosta (da ne lažem, ne znam napamet rješenja svih, pa čak ni dosta velikog dijela zadataka :D) ovih nejednakosti u zadaći mi se čini relativno jednoidejna, tj. primijeniš nešto i odmah si na kraju. :)
Da, obično na kraju zadaće budu teži zadaci koji baš i nisu potpuno obrađeni gradivom na nastavi. Zato (according to Lepi) i možete izabrati pet zadataka i predati ih. 
Koliko vidim, neki (većina?) zadataka tu se mogu riješiti s nejednakostima sredina (u 18., su u pitanju, čini mi se, A-H i A-G, a nisam vidio da se negdje spominju nejednakosti sredina u svom općenitom obliku). Neki dokazi vjerojatno mogu i indukcijom, makar mi se ne čini baš trivijalno. E, da, čisto ako ćete rješavati, ako se ne varam, vidio sam tipfelere u 18. zadatku (naravno, u nazivniku prve nejednakosti je 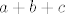 ) i 24. zadatku (sve vrijedi, samo se ) i 24. zadatku (sve vrijedi, samo se 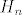 zove harmonijska, a ne kvadratna sredina). zove harmonijska, a ne kvadratna sredina).
Uglavnom, neki zadaci će biti poznati ljudima koji su se pripremali za natjecanja u srednjoj školi (Cauchy-Schwarz-Bunyakovsky, K-A-G-H itd.). Ako vas zanima, našao sam par linkova gdje možete vidjeti neke poznate nejednakosti (s tim da se tamo obrađuje puno veći broj poznatih i relativno teških nejednakosti, tu u zadaći vjerojatno ne treba velika većina toga). Kao što rekoh, ta je tema dosta popularna na raznim natjecanjima iz matematike (pogotovo na višim razinama pa sve do međunarodnih tipa IMO i sl.), tako da ima dosta razumljivih stvari po Internetu. 
S tim da se nemojte uplašiti - dosta (da ne lažem, ne znam napamet rješenja svih, pa čak ni dosta velikog dijela zadataka  ) ovih nejednakosti u zadaći mi se čini relativno jednoidejna, tj. primijeniš nešto i odmah si na kraju. ) ovih nejednakosti u zadaći mi se čini relativno jednoidejna, tj. primijeniš nešto i odmah si na kraju. 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:06 pet, 8. 10. 2010 Naslov: Postano: 18:06 pet, 8. 10. 2010 Naslov: |
    |
|
|
Ne bih rekao da očekuju, te stvari su u zadaćama već (minimalno) treću godinu i do sada nisu pokazivale neku sposobnost da se prošire i na sferu kolokvija (a u zadaći ih, dakako, možeš izbjeći). Mislim da je to više kao nekakav poticaj onima koje zanimaju malo teže stvari, a na kolokvijima i usmenima je najbitnije gradivo spomenuto na vježbama i predavanjima. (Mislim, ne jamčim ja to i ne tvrdim da nema nekih iznimaka, samo pretpostavljam. :lol: Ja sam na usmenom odgovarao, među ostalim, nešto što, koliko znam, nismo spomenuli ni na predavanjima ni na vježbama, ali je bilo rečeno u srednjoj školi, nije bilo teško i usto se lako dalo izvesti samo od sebe.) Ako sam dobro čuo, ove bi se godine nakon tri godine mogla vratiti neobavezna natjecanja za dodatne bodove, a pretpostavljam da će se onda teže stvari pojavljivati tamo.
A evo hint za 11. - pretpostavi suprotno, kvadriraj, pogledaj što dobivaš i na taj način jednostavno pokaži da i [latex]\sqrt{n}[/latex] mora biti racionalan. E, sad, o tome ste vjerojatno već raspravljali na Analizi ili Elementarnoj. Može se dokazati da [latex]\sqrt{n}\in\mathbb{Q}[/latex] znači da je [latex]n[/latex] nužno kvadrat cijelog broja. (Nije teško, zbilja nije, općeniti princip je isti kao kad ste, a pretpostavljam da jeste, pokazivali da je [latex]\sqrt{2}[/latex] iracionalan.) Dakle, imaš da je [latex]n=k^2[/latex] i pretpostavili smo da je [latex]\sqrt{n+\sqrt{n}}=\sqrt{k+k^2}[/latex] racionalan. Sad, opet, koristeći istu tvrdnju kao gore, možemo zaključiti da je [latex]k+k^2[/latex] kvadrat prirodnog broja. I sad samo dokaži da je to nemoguće (hint: smještanje između dva uzastopna kvadrata cijelih brojeva - to je inače relativno česta strategija u problemima s kvadratima i sl.). Evo, reci ako trebaju neki detaljniji hintovi. :)
Ne bih rekao da očekuju, te stvari su u zadaćama već (minimalno) treću godinu i do sada nisu pokazivale neku sposobnost da se prošire i na sferu kolokvija (a u zadaći ih, dakako, možeš izbjeći). Mislim da je to više kao nekakav poticaj onima koje zanimaju malo teže stvari, a na kolokvijima i usmenima je najbitnije gradivo spomenuto na vježbama i predavanjima. (Mislim, ne jamčim ja to i ne tvrdim da nema nekih iznimaka, samo pretpostavljam.  Ja sam na usmenom odgovarao, među ostalim, nešto što, koliko znam, nismo spomenuli ni na predavanjima ni na vježbama, ali je bilo rečeno u srednjoj školi, nije bilo teško i usto se lako dalo izvesti samo od sebe.) Ako sam dobro čuo, ove bi se godine nakon tri godine mogla vratiti neobavezna natjecanja za dodatne bodove, a pretpostavljam da će se onda teže stvari pojavljivati tamo. Ja sam na usmenom odgovarao, među ostalim, nešto što, koliko znam, nismo spomenuli ni na predavanjima ni na vježbama, ali je bilo rečeno u srednjoj školi, nije bilo teško i usto se lako dalo izvesti samo od sebe.) Ako sam dobro čuo, ove bi se godine nakon tri godine mogla vratiti neobavezna natjecanja za dodatne bodove, a pretpostavljam da će se onda teže stvari pojavljivati tamo.
A evo hint za 11. - pretpostavi suprotno, kvadriraj, pogledaj što dobivaš i na taj način jednostavno pokaži da i  mora biti racionalan. E, sad, o tome ste vjerojatno već raspravljali na Analizi ili Elementarnoj. Može se dokazati da mora biti racionalan. E, sad, o tome ste vjerojatno već raspravljali na Analizi ili Elementarnoj. Može se dokazati da 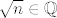 znači da je znači da je  nužno kvadrat cijelog broja. (Nije teško, zbilja nije, općeniti princip je isti kao kad ste, a pretpostavljam da jeste, pokazivali da je nužno kvadrat cijelog broja. (Nije teško, zbilja nije, općeniti princip je isti kao kad ste, a pretpostavljam da jeste, pokazivali da je 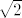 iracionalan.) Dakle, imaš da je iracionalan.) Dakle, imaš da je 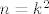 i pretpostavili smo da je i pretpostavili smo da je 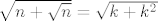 racionalan. Sad, opet, koristeći istu tvrdnju kao gore, možemo zaključiti da je racionalan. Sad, opet, koristeći istu tvrdnju kao gore, možemo zaključiti da je 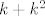 kvadrat prirodnog broja. I sad samo dokaži da je to nemoguće (hint: smještanje između dva uzastopna kvadrata cijelih brojeva - to je inače relativno česta strategija u problemima s kvadratima i sl.). Evo, reci ako trebaju neki detaljniji hintovi. kvadrat prirodnog broja. I sad samo dokaži da je to nemoguće (hint: smještanje između dva uzastopna kvadrata cijelih brojeva - to je inače relativno česta strategija u problemima s kvadratima i sl.). Evo, reci ako trebaju neki detaljniji hintovi. 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 12:59 sub, 9. 10. 2010 Naslov: Postano: 12:59 sub, 9. 10. 2010 Naslov: |
    |
|
|
Hvala! Shvatio sam sad taj dokaz.
Još jedno pitanje:
sin^4(x) + cos^4(x) > a, za a element od [0, 1]...
Mogu ljepše napisati ovaj sin^4(x) + cos^4(x) kao
(sin^2(x) + cos^2(x)) - 2sin^2(x)cos^2(x)... ma uglavnom, da ne duljim, mogu dotjerati taj izraz do toga da mi ostane samo sinus (ili kosinus, votevr).
Zapravo me ovaj ''a'' muči, ne znam kako bih sad oko njega to... Može još malo hintova? xD
Hvala! Shvatio sam sad taj dokaz.
Još jedno pitanje:
sin^4(x) + cos^4(x) > a, za a element od [0, 1]...
Mogu ljepše napisati ovaj sin^4(x) + cos^4(x) kao
(sin^2(x) + cos^2(x)) - 2sin^2(x)cos^2(x)... ma uglavnom, da ne duljim, mogu dotjerati taj izraz do toga da mi ostane samo sinus (ili kosinus, votevr).
Zapravo me ovaj ''a'' muči, ne znam kako bih sad oko njega to... Može još malo hintova? xD
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 14:57 sub, 9. 10. 2010 Naslov: Postano: 14:57 sub, 9. 10. 2010 Naslov: |
    |
|
|
Ha mislim, nema tu baš nekog pametnog hinta, došao si praktički do kraja. Dobio si, dakle, da je taj izraz na lijevoj strani jednak [latex]\displaystyle\frac{\cos (4x)+3}{4}[/latex]. Dakle, želiš [latex]\cos (4x)>4a-3[/latex], što bi reklo da moraš imati [latex]\cos (4x)\in\langle 4a-3,1\][/latex] (specijalno, za [latex]a=1[/latex] nema rješenja jer je nemoguće imati [latex]\cos (4x)>1[/latex]).
A dobro, sad bih ja zapravo tu gledao nekakva dva slučaja (čisto što se tiče zapisa, dosta je jasno da želiš sad nekako primijeniti [latex]\mathrm{arccos}[/latex] na ovaj izraz, samo malo moramo paziti na domenu te funkcije).
Ako je [latex]4a-3<-1[/latex] (što je ekvivalentno s [latex]a<0.5[/latex]), vidimo da nam [latex]\cos (4x)[/latex] može biti bilo koji broj od [latex]-1[/latex] do [latex]1[/latex] (uključivo). Naravno, to se uvijek postiže, pa je tu skup rješenja [latex]\mathbb{R}[/latex].
S druge strane, ako je [latex]1>4a-3\geq -1[/latex], probaj sad nacrtati situaciju [latex]\cos (4x)\in\langle 4a-3,1\][/latex] na kružnici ili kako već. Kao što rekoh, prirodna je ideja primijeniti arkus kosinus na taj izraz (samo moramo biti pažljivi oko toga gdje su nam rubovi) - dobivamo da vrijedi [latex]4x\in\langle -\mathrm{arccos}(4a-3)+2k\pi, \mathrm{arccos}(4a-3)+2k\pi\rangle[/latex] za [latex]k\in\mathbb{Z}[/latex], ako sam si ja to sad dobro zamislio u glavi. :) (Primijeti da je za [latex]a=0.5[/latex] to jedan vrlo poseban skup. :))
Slučaj [latex]4a-3=1[/latex] smo već riješili, a ostalih slučajeva nema. Dakle, skupovi rješenja bi po meni trebali biti [latex]\mathbb{R}[/latex] za [latex]a\in\[0,0.5\rangle[/latex], [latex]\displaystyle\bigcup_{k\in\mathbb{Z}}\langle \displaystyle\frac{-\mathrm{arccos}(4a-3)+2k\pi}{4}, \displaystyle\frac{\mathrm{arccos}(4a-3)+2k\pi}{4}\rangle[/latex] za [latex]0.5\leq a<1[/latex] i [latex]\emptyset[/latex] za [latex]a=1[/latex].
Evo, (djelomično namjerno) nisam bio preprecizan i detaljan, ali sam zato dao rezultate da provjeriš. Eto... pitaj ako nije bilo dovoljno. :)
Ha mislim, nema tu baš nekog pametnog hinta, došao si praktički do kraja. Dobio si, dakle, da je taj izraz na lijevoj strani jednak 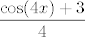 . Dakle, želiš . Dakle, želiš  , što bi reklo da moraš imati , što bi reklo da moraš imati 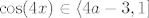 (specijalno, za (specijalno, za 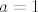 nema rješenja jer je nemoguće imati nema rješenja jer je nemoguće imati 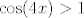 ). ).
A dobro, sad bih ja zapravo tu gledao nekakva dva slučaja (čisto što se tiče zapisa, dosta je jasno da želiš sad nekako primijeniti 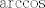 na ovaj izraz, samo malo moramo paziti na domenu te funkcije). na ovaj izraz, samo malo moramo paziti na domenu te funkcije).
Ako je 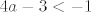 (što je ekvivalentno s (što je ekvivalentno s 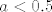 ), vidimo da nam ), vidimo da nam 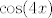 može biti bilo koji broj od može biti bilo koji broj od  do do  (uključivo). Naravno, to se uvijek postiže, pa je tu skup rješenja (uključivo). Naravno, to se uvijek postiže, pa je tu skup rješenja  . .
S druge strane, ako je 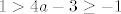 , probaj sad nacrtati situaciju , probaj sad nacrtati situaciju 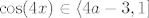 na kružnici ili kako već. Kao što rekoh, prirodna je ideja primijeniti arkus kosinus na taj izraz (samo moramo biti pažljivi oko toga gdje su nam rubovi) - dobivamo da vrijedi na kružnici ili kako već. Kao što rekoh, prirodna je ideja primijeniti arkus kosinus na taj izraz (samo moramo biti pažljivi oko toga gdje su nam rubovi) - dobivamo da vrijedi 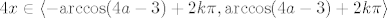 za za 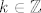 , ako sam si ja to sad dobro zamislio u glavi. , ako sam si ja to sad dobro zamislio u glavi.  (Primijeti da je za (Primijeti da je za  to jedan vrlo poseban skup. to jedan vrlo poseban skup.  ) )
Slučaj 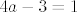 smo već riješili, a ostalih slučajeva nema. Dakle, skupovi rješenja bi po meni trebali biti smo već riješili, a ostalih slučajeva nema. Dakle, skupovi rješenja bi po meni trebali biti  za za 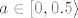 , , 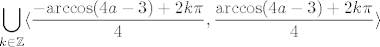 za za 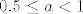 i i  za za 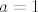 . .
Evo, (djelomično namjerno) nisam bio preprecizan i detaljan, ali sam zato dao rezultate da provjeriš. Eto... pitaj ako nije bilo dovoljno. 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
|

















