| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
 Postano: 14:52 pet, 15. 10. 2010 Naslov: Zadatak s demonstratura Postano: 14:52 pet, 15. 10. 2010 Naslov: Zadatak s demonstratura |
    |
|
|
Evo kontraprimjera koji sam ostao duzan na demonstraturama, vezan za zadatak u kojem treba provjeriti je li skup [latex]\;S=\{(x_1,x_2,x_3) \in C^3 : \; (x_1^2-x_2^2)\cdot\;x_3^2\; \in \;R\}[/latex] potprostor u [latex]C^3[/latex]. Cini nam se da nije, pa pokusavamo naci [latex]\alpha \in C[/latex] t.d. nam vektor [latex]\;\; \alpha(x_1,x_2,x_3)[/latex] ne bude u S. To znaci da [latex]\;\;[({\alpha}x_1)^2-({\alpha}x_2)^2]\cdot({\alpha}x_3)^2 \notin R[/latex] tj. da [latex]{\alpha}^4\notin R[/latex], pa uzmemo npr. [latex]\alpha=i^{1/4}[/latex] i vektor [latex](1,0,1)[/latex]. Tada ocito [latex]i^{1/4}\cdot(1,0,1) \notin S[/latex], dakle S nije potprostor jer nije zadovoljena homogenost.
Evo kontraprimjera koji sam ostao duzan na demonstraturama, vezan za zadatak u kojem treba provjeriti je li skup 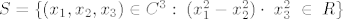 potprostor u potprostor u 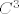 . Cini nam se da nije, pa pokusavamo naci . Cini nam se da nije, pa pokusavamo naci 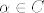 t.d. nam vektor t.d. nam vektor 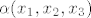 ne bude u S. To znaci da ne bude u S. To znaci da 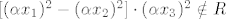 tj. da tj. da 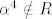 , pa uzmemo npr. , pa uzmemo npr. 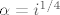 i vektor i vektor 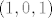 . Tada ocito . Tada ocito 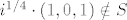 , dakle S nije potprostor jer nije zadovoljena homogenost. , dakle S nije potprostor jer nije zadovoljena homogenost.
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
 Postano: 23:01 sri, 20. 10. 2010 Naslov: Postano: 23:01 sri, 20. 10. 2010 Naslov: |
    |
|
|
Evo nastavljam s zadacima koje sam ostao duzan:
Radi se o trecem iz 2. zadace, naime, objasnit cu koncept, a detaljan raspis ostavljam vama, ako ce trebat i za demonstrature u petak.
Krenemo prema uputi, dakle trazimo potprostore [latex]M_1[/latex] i [latex]M_2[/latex] te [latex]M_1+M_2[/latex] iz kojeg zakljucujemo mogucnost trazenog raspisa.
[latex]q\;\in\;M_1,\; q(x)\;=\;a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0[/latex], a iz uvjeta [latex]q(t_1)\;=\;0 \implies \{x^n-t_1^n,x^{n-1}-t_1^{n-1},...,x-t_1\}[/latex] baza za [latex]M_1[/latex]. Analogno za potprostor [latex]M_2[/latex], pa imamo bazu za [latex]M_1+M_2[/latex], npr. [latex]\{baza \;za\; M_1, x-t_2\}[/latex], znaci [latex]\;dim(M_1+M_2)\;=\;n+1\;=\;dim(P_n)[/latex] i zakljucujemo kako je trazeni raspis moguc, no nikako nije jedinstven, jer je [latex]dim(M_1\cap M_2)\;=\;n-1[/latex].
Evo nastavljam s zadacima koje sam ostao duzan:
Radi se o trecem iz 2. zadace, naime, objasnit cu koncept, a detaljan raspis ostavljam vama, ako ce trebat i za demonstrature u petak.
Krenemo prema uputi, dakle trazimo potprostore 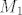 i i 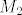 te te  iz kojeg zakljucujemo mogucnost trazenog raspisa. iz kojeg zakljucujemo mogucnost trazenog raspisa.
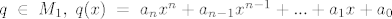 , a iz uvjeta , a iz uvjeta 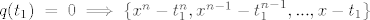 baza za baza za 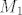 . Analogno za potprostor . Analogno za potprostor  , pa imamo bazu za , pa imamo bazu za  , npr. , npr. 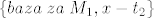 , znaci , znaci 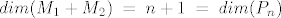 i zakljucujemo kako je trazeni raspis moguc, no nikako nije jedinstven, jer je i zakljucujemo kako je trazeni raspis moguc, no nikako nije jedinstven, jer je 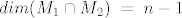 . .
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
 Postano: 13:04 čet, 28. 10. 2010 Naslov: Postano: 13:04 čet, 28. 10. 2010 Naslov: |
    |
|
|
Nacin dobivanja baze za sumu potprostora je uvijek isti, ubacis obje baze u isti skup i reduciras ga do lin. nezavisnog. U nasem slucaju, provjerimo jesu li svi elementi baze za [latex]M_1[/latex] nezavisni sa [latex]x-t_2\in M_2[/latex], sto jesu, dakle u [latex]M_1+M_2\le P_n[/latex] nasli smo linearno nezavisan skup sa n+1 elemenata, pa je on nuzno baza za [latex]M_1+M_2[/latex]. Tada je po formuli dokazanoj na predavanjima:
[latex]dim(M_1\cap M_2)=dim(M_1)+dim(M_2)-dim(M_1+M_2)=n-1[/latex].
Nacin dobivanja baze za sumu potprostora je uvijek isti, ubacis obje baze u isti skup i reduciras ga do lin. nezavisnog. U nasem slucaju, provjerimo jesu li svi elementi baze za 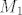 nezavisni sa nezavisni sa 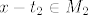 , sto jesu, dakle u , sto jesu, dakle u 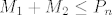 nasli smo linearno nezavisan skup sa n+1 elemenata, pa je on nuzno baza za nasli smo linearno nezavisan skup sa n+1 elemenata, pa je on nuzno baza za  . Tada je po formuli dokazanoj na predavanjima: . Tada je po formuli dokazanoj na predavanjima:
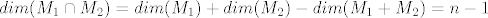 . .
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
 Postano: 22:00 čet, 28. 10. 2010 Naslov: Postano: 22:00 čet, 28. 10. 2010 Naslov: |
    |
|
|
Ja imam pitanje nevezano uz zadacu.. ugl. buni me malo definicija linearne ljuske nekog skupa. Pa da mi etko
kaze jesam li ja to dobro shvatila- Znaci, linearna ljuska nekog skupa je skup koji sadrzi sve linearne kombinacije tog zadanog skupa?? Npr. U prostoru R^3 odaberemo a_1=(1,7,0) i a_2=(-1,2,0) i sad [{a_1,a_2}]={(0,9,0),(1,5,0)} ? jel to to il sam krivo razumjela?
Ja imam pitanje nevezano uz zadacu.. ugl. buni me malo definicija linearne ljuske nekog skupa. Pa da mi etko
kaze jesam li ja to dobro shvatila- Znaci, linearna ljuska nekog skupa je skup koji sadrzi sve linearne kombinacije tog zadanog skupa?? Npr. U prostoru R^3 odaberemo a_1=(1,7,0) i a_2=(-1,2,0) i sad [{a_1,a_2}]={(0,9,0),(1,5,0)} ? jel to to il sam krivo razumjela?
|
|
| [Vrh] |
|
Bruno^_^
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (20:22:27)
Postovi: (1D)16
|
 Postano: 22:28 čet, 28. 10. 2010 Naslov: Postano: 22:28 čet, 28. 10. 2010 Naslov: |
    |
|
|
[quote]Znaci, linearna ljuska nekog skupa je skup koji sadrzi sve linearne kombinacije tog zadanog skupa[/quote]
U biti da, no nije mi jasno kako si ovo dobila:
[quote]U prostoru R^3 odaberemo a_1=(1,7,0) i a_2=(-1,2,0) i sad [{a_1,a_2}]={(0,9,0),(1,5,0)}[/quote]
Linearnih kombinacije od a_1 i a_2 ima beskonacno (to nisu samo zbrajanje i oduzimanje dva vektora kao sto se da naslutiti iz tvog skupa), tako da taj skup ne moze biti konacan! opcenito, u tvom primjeru je [{a_1, a_2}]={(x, y, 0) : x,y e R}, odnosno skup svih točaka ravnine.
Poanta ovog je da za proizvoljne x,y realne brojeve (koje god odaberes) uvijek mozes naci (jedinstvene) koeficijente tako da je linearna kombinacija od a_1 i a_2 jednaka (x,y,0). Jasnije ili? :D
| Citat: | | Znaci, linearna ljuska nekog skupa je skup koji sadrzi sve linearne kombinacije tog zadanog skupa |
U biti da, no nije mi jasno kako si ovo dobila:
| Citat: | | U prostoru R^3 odaberemo a_1=(1,7,0) i a_2=(-1,2,0) i sad [{a_1,a_2}]={(0,9,0),(1,5,0)} |
Linearnih kombinacije od a_1 i a_2 ima beskonacno (to nisu samo zbrajanje i oduzimanje dva vektora kao sto se da naslutiti iz tvog skupa), tako da taj skup ne moze biti konacan! opcenito, u tvom primjeru je [{a_1, a_2}]={(x, y, 0) : x,y e R}, odnosno skup svih točaka ravnine.
Poanta ovog je da za proizvoljne x,y realne brojeve (koje god odaberes) uvijek mozes naci (jedinstvene) koeficijente tako da je linearna kombinacija od a_1 i a_2 jednaka (x,y,0). Jasnije ili? 
|
|
| [Vrh] |
|
bekse
Forumaš(ica)

Pridružen/a: 06. 11. 2009. (18:19:09)
Postovi: (19)16
|
 Postano: 22:31 čet, 28. 10. 2010 Naslov: Postano: 22:31 čet, 28. 10. 2010 Naslov: |
    |
|
|
Izgleda da si krivo razumjela, tj. linearna ljuska nekog skupa zbilja je skup svih vektora koji se mogu prikazati kao linearna kombinacija elemenata tog doticnog skupa, ali u ovom konkretnom slucaju si krivo napisala jer linerane kombinacije elemenata nekog skupa podrazumijevaju sva moguca zbrajanja, oduzimanja i mnozenja skalarom iz polja, a ne samo zbroj i razliku tih vektora kao sto si ti napisala (iako ovaj drugi cak ni nije njihova razlika, ali pretpostavljam da si mislila napisati (2,5,0)).
Dakle linearna ljuska ovog skupa {a1,a2} su svi vektori oblika A*a1+B*a2 pri cemu su A i B naravno iz polja nad kojim je doticni vektorski prostor zadan.
Izgleda da si krivo razumjela, tj. linearna ljuska nekog skupa zbilja je skup svih vektora koji se mogu prikazati kao linearna kombinacija elemenata tog doticnog skupa, ali u ovom konkretnom slucaju si krivo napisala jer linerane kombinacije elemenata nekog skupa podrazumijevaju sva moguca zbrajanja, oduzimanja i mnozenja skalarom iz polja, a ne samo zbroj i razliku tih vektora kao sto si ti napisala (iako ovaj drugi cak ni nije njihova razlika, ali pretpostavljam da si mislila napisati (2,5,0)).
Dakle linearna ljuska ovog skupa {a1,a2} su svi vektori oblika A*a1+B*a2 pri cemu su A i B naravno iz polja nad kojim je doticni vektorski prostor zadan.
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
Buki
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (20:15:17)
Postovi: (56)16
|
 Postano: 15:34 pon, 1. 11. 2010 Naslov: Postano: 15:34 pon, 1. 11. 2010 Naslov: |
    |
|
|
[quote="genchy"]Evo nastavljam s zadacima koje sam ostao duzan:
Radi se o trecem iz 2. zadace, naime, objasnit cu koncept, a detaljan raspis ostavljam vama, ako ce trebat i za demonstrature u petak.
Krenemo prema uputi, dakle trazimo potprostore [latex]M_1[/latex] i [latex]M_2[/latex] te [latex]M_1+M_2[/latex] iz kojeg zakljucujemo mogucnost trazenog raspisa.
[latex]q\;\in\;M_1,\; q(x)\;=\;a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0[/latex], a iz uvjeta [latex]q(t_1)\;=\;0 \implies \{x^n-t_1^n,x^{n-1}-t_1^{n-1},...,x-t_1\}[/latex] baza za [latex]M_1[/latex]. Analogno za potprostor [latex]M_2[/latex], pa imamo bazu za [latex]M_1+M_2[/latex], npr. [latex]\{baza \;za\; M_1, x-t_2\}[/latex], znaci [latex]\;dim(M_1+M_2)\;=\;n+1\;=\;dim(P_n)[/latex] i zakljucujemo kako je trazeni raspis moguc, no nikako nije jedinstven, jer je [latex]dim(M_1\cap M_2)\;=\;n-1[/latex].[/quote]
možeš li objasniti otkud ti baza za m1? šta izjednačujemo uvjete ili.-.?
| genchy (napisa): | Evo nastavljam s zadacima koje sam ostao duzan:
Radi se o trecem iz 2. zadace, naime, objasnit cu koncept, a detaljan raspis ostavljam vama, ako ce trebat i za demonstrature u petak.
Krenemo prema uputi, dakle trazimo potprostore 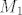 i i 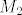 te te  iz kojeg zakljucujemo mogucnost trazenog raspisa. iz kojeg zakljucujemo mogucnost trazenog raspisa.
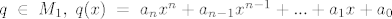 , a iz uvjeta , a iz uvjeta 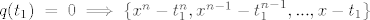 baza za baza za 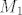 . Analogno za potprostor . Analogno za potprostor 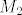 , pa imamo bazu za , pa imamo bazu za  , npr. , npr. 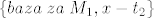 , znaci , znaci 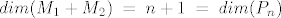 i zakljucujemo kako je trazeni raspis moguc, no nikako nije jedinstven, jer je i zakljucujemo kako je trazeni raspis moguc, no nikako nije jedinstven, jer je 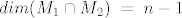 . . |
možeš li objasniti otkud ti baza za m1? šta izjednačujemo uvjete ili.-.?
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
 Postano: 15:41 pon, 1. 11. 2010 Naslov: Postano: 15:41 pon, 1. 11. 2010 Naslov: |
    |
|
|
Iz uvjeta da je [latex]q(t_1)=0[/latex] dobivamo slobodni clan, njega ubacimo u pocetni oblik polinoma [latex]q[/latex] i izlucivanjem koeficijenata [latex]a_n,a_{n-1},...,a_1[/latex] imamo s.i. za [latex]M_1[/latex], no ocito su nezavisni, pa cine bazu.
Iz uvjeta da je 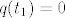 dobivamo slobodni clan, njega ubacimo u pocetni oblik polinoma dobivamo slobodni clan, njega ubacimo u pocetni oblik polinoma  i izlucivanjem koeficijenata i izlucivanjem koeficijenata 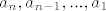 imamo s.i. za imamo s.i. za 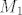 , no ocito su nezavisni, pa cine bazu. , no ocito su nezavisni, pa cine bazu.
|
|
| [Vrh] |
|
Buki
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (20:15:17)
Postovi: (56)16
|
 Postano: 15:46 pon, 1. 11. 2010 Naslov: Postano: 15:46 pon, 1. 11. 2010 Naslov: |
    |
|
|
[quote="genchy"]Iz uvjeta da je [latex]q(t_1)=0[/latex] dobivamo slobodni clan, njega ubacimo u pocetni oblik polinoma [latex]q[/latex] i izlucivanjem koeficijenata [latex]a_n,a_{n-1},...,a_1[/latex] imamo s.i. za [latex]M_1[/latex], no ocito su nezavisni, pa cine bazu.[/quote]
a kako znas da je taj clan 0?
| genchy (napisa): | Iz uvjeta da je 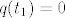 dobivamo slobodni clan, njega ubacimo u pocetni oblik polinoma dobivamo slobodni clan, njega ubacimo u pocetni oblik polinoma  i izlucivanjem koeficijenata i izlucivanjem koeficijenata 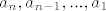 imamo s.i. za imamo s.i. za 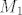 , no ocito su nezavisni, pa cine bazu. , no ocito su nezavisni, pa cine bazu. |
a kako znas da je taj clan 0?
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
dluinovic
Forumaš(ica)


Pridružen/a: 23. 02. 2006. (15:53:39)
Postovi: (5)16
Spol: 
|
 Postano: 2:20 čet, 4. 11. 2010 Naslov: Postano: 2:20 čet, 4. 11. 2010 Naslov: |
    |
|
|
[quote="Buki"][quote="genchy"]Iz uvjeta da je [latex]q(t_1)=0[/latex] dobivamo slobodni clan, njega ubacimo u pocetni oblik polinoma [latex]q[/latex] i izlucivanjem koeficijenata [latex]a_n,a_{n-1},...,a_1[/latex] imamo s.i. za [latex]M_1[/latex], no ocito su nezavisni, pa cine bazu.[/quote]
a kako znas da je taj clan 0?[/quote]
Mene je mučilo nešto slično, ali stvar ti je u tome da ti ne znas da je taj član slobodni jednak 0,
nego znas da je q(t1)=0 iz definicije potprostora M1,
i onda kada to uvrstis t1 u q(x)--> dobijes da je
q(t1)=[latex]a_n[/latex]t1^n + [latex]a_{n-1}[/latex]t1^(n-1) + ...[latex]a_1[/latex]t1 + [latex]a_0[/latex]=(ali iz uvjeta znas da je to nula)=0
I onda izrazis prebacivanjem svega ostaloga na drugu stranu slobodni član (a0 je slobodni član,npr. neki broj 1,2,3 ili kaj god) [latex]a_0[/latex]=-[latex]a_n[/latex]t^n - [latex]a_{n-1}[/latex]t^(n-1) - .... -[latex]a_1[/latex]t^1
E, taj dio je meni bio totalno zbunjujuc, i drito mi je sada puno jasnije nakon sto sam pročitao tvoje fantastično pitanjce i genchyeve odgovore i objasnjenja, da ste mi blizu izljubio bi vas oboje ;) koliko sam sretan.
Uglavnom onda imamo da je kada sada znamo iz početnog uvjeta "koliko" nam je taj član a0 izraženo ovom formulom, onda to uvrstim fino u početnu jednadžbu za q(x)€M1, pa to izgleda ovako:
q( x )=[latex]a_n[/latex]x^n + [latex]a_{n-1}[/latex]x^(n-1) + ...[latex]a_1[/latex]x^1 - [latex]a_n[/latex]t^n -[latex]a_{n-1}[/latex]t^(n-1) - .... - [latex]a_1[/latex]t^1
Potom, iz svega izlučiš koeficijente s istim indeksima [latex]a_n[/latex] i dobiješ formulu opću za q(x) sređenu:
q( x )=[latex]a_n[/latex](x^n - t^n) + [latex]a_{n-1}[/latex](x^(n-1) - t^(n-1) + ...[latex]a_1[/latex](x^1 - t^1)
Na kraju iz toga dobijemo kako je rekao genchy da je
[latex]\;\implies \{x^n-t_1^n,x^{n-1}-t_1^{n-1},...,x-t_1\}[/latex] baza za [latex]M_1[/latex].
A sada, zašto je to baza za M1, pa meni su ovi polinomi u LA stvarno znali biti zbunjujući, ali ja MISLIM da je to baza zato što nijedan od ovih polinoma zasebno očito po mojem mišljenju ne možeš dobiti pomoću drugih linearnim kombinacijama jer s naprosto različitih potencija i sve i da si Merlin nemreš dobiti x^n zbrajanjem polinoma stp<n.Ako samo pogriješio u rezoniranju tu negdje cijenim svaku povratnu informaciju ili proširenje na ono što sam rekao.
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
[quote="genchy"]Evo nastavljam s zadacima koje sam ostao duzan:
Radi se o trecem iz 2. zadace, naime, objasnit cu koncept, a detaljan raspis ostavljam vama, ako ce trebat i za demonstrature u petak.
Krenemo prema uputi, dakle trazimo potprostore [latex]M_1[/latex] i [latex]M_2[/latex] te [latex]M_1+M_2[/latex] iz kojeg zakljucujemo mogucnost trazenog raspisa.
[latex]q\;\in\;M_1,\; q(x)\;=\;a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0[/latex], a iz uvjeta [latex]q(t_1)\;=\;0 \implies \{x^n-t_1^n,x^{n-1}-t_1^{n-1},...,x-t_1\}[/latex] baza za [latex]M_1[/latex]. Analogno za potprostor [latex]M_2[/latex], pa imamo bazu za [latex]M_1+M_2[/latex], npr. [latex]\{baza \;za\; M_1, x-t_2\}[/latex], znaci [latex]\;dim(M_1+M_2)\;=\;n+1\;=\;dim(P_n)[/latex] i zakljucujemo kako je trazeni raspis moguc, no nikako nije jedinstven, jer je [latex]dim(M_1\cap M_2)\;=\;n-1[/latex].[/quote]
E, hvala ti puno čovječe, sada mi je taj zadatak jasan potpuno, kada sam pročitao sve tvoje postove vezane za taj zadatak.
[size=9][color=#999999]Added after 39 minutes:[/color][/size]
[quote="888"]jel možeš malo detaljnije objasnit kako si našao bazu za M+L, nije mi jasno zašto {baza za M,x-t2} i ovo zadnje zašto je M1 presjek M2=n-1...[/quote]
Ukoliko sam ja to shvatio, onda prema genchyu, dodaš jedan vektor iz baze za M2 u M1 i provjeriš je li to linearno nezavisan skup, budući da je dim(M1)=dim(M2)=n čim dodaš još jedan vektor u M1, ako su oni potom linearno nezavisni svi iz baze M1, s npr, tim x-t2 slijedi da M1+M2 je baza i razapinje cijeli P_n jer je dim(M1+M2)=n+1 kao i P_n.
A ja sam to sebi pojasnio(čitaj dalje:PO MOJEM MIŠLJENJU) tako što je to moguće samo zbog tog početnog uvjeta zadatka koji nam kaže da je t1!=t2, pa sam si razmišljao ovako, postoji li neki broj npr. a€R takav da je u a(x-t1)=x-t2, pa sam uvrstio brojeve jer je t1 različit od t2 ovako:
a(x-t1)=x-t2;t1=3,t2=4;
a(x-3)=x-4 i dobijemo
ax-3a=x-4 (po tm o jednakosti polinoma, oni su jednaki
ako i samo ako su im svi koeficijenti jednaki)
no to povlači da bi istovremeno moralo biti a=1 i a=4/3 a to je =><= kontradikcija, ako nisam negdje pogrijesio u razmisljanju.
Također, sigurno ne postoji neki niz a_i eva iz R takvih da bi x-t2 bio linearna kombinacija vektora baze za M1 koji sadrze i polinome stp veceg od 1.I onda se vidi čak da je bilo t1=t2 u uvjetu zadatka da to ne bi bilo moguće reći.
| Buki (napisa): | | genchy (napisa): | Iz uvjeta da je 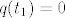 dobivamo slobodni clan, njega ubacimo u pocetni oblik polinoma dobivamo slobodni clan, njega ubacimo u pocetni oblik polinoma  i izlucivanjem koeficijenata i izlucivanjem koeficijenata 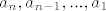 imamo s.i. za imamo s.i. za 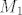 , no ocito su nezavisni, pa cine bazu. , no ocito su nezavisni, pa cine bazu. |
a kako znas da je taj clan 0? |
Mene je mučilo nešto slično, ali stvar ti je u tome da ti ne znas da je taj član slobodni jednak 0,
nego znas da je q(t1)=0 iz definicije potprostora M1,
i onda kada to uvrstis t1 u q(x)→ dobijes da je
q(t1)=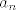 t1^n + t1^n + 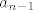 t1^(n-1) + ... t1^(n-1) + ...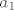 t1 + t1 + 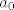 =(ali iz uvjeta znas da je to nula)=0 =(ali iz uvjeta znas da je to nula)=0
I onda izrazis prebacivanjem svega ostaloga na drugu stranu slobodni član (a0 je slobodni član,npr. neki broj 1,2,3 ili kaj god) 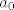 =- =-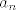 t^n - t^n - 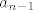 t^(n-1) - .... - t^(n-1) - .... -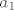 t^1 t^1
E, taj dio je meni bio totalno zbunjujuc, i drito mi je sada puno jasnije nakon sto sam pročitao tvoje fantastično pitanjce i genchyeve odgovore i objasnjenja, da ste mi blizu izljubio bi vas oboje  koliko sam sretan. koliko sam sretan.
Uglavnom onda imamo da je kada sada znamo iz početnog uvjeta "koliko" nam je taj član a0 izraženo ovom formulom, onda to uvrstim fino u početnu jednadžbu za q(x)€M1, pa to izgleda ovako:
q( x )=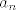 x^n + x^n + 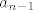 x^(n-1) + ... x^(n-1) + ...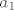 x^1 - x^1 - 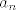 t^n - t^n -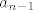 t^(n-1) - .... - t^(n-1) - .... - 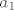 t^1 t^1
Potom, iz svega izlučiš koeficijente s istim indeksima 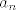 i dobiješ formulu opću za q(x) sređenu: i dobiješ formulu opću za q(x) sređenu:
q( x )=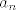 (x^n - t^n) + (x^n - t^n) + 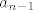 (x^(n-1) - t^(n-1) + ... (x^(n-1) - t^(n-1) + ...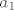 (x^1 - t^1) (x^1 - t^1)
Na kraju iz toga dobijemo kako je rekao genchy da je
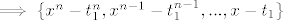 baza za baza za 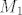 . .
A sada, zašto je to baza za M1, pa meni su ovi polinomi u LA stvarno znali biti zbunjujući, ali ja MISLIM da je to baza zato što nijedan od ovih polinoma zasebno očito po mojem mišljenju ne možeš dobiti pomoću drugih linearnim kombinacijama jer s naprosto različitih potencija i sve i da si Merlin nemreš dobiti x^n zbrajanjem polinoma stp<n.Ako samo pogriješio u rezoniranju tu negdje cijenim svaku povratnu informaciju ili proširenje na ono što sam rekao.
Added after 6 minutes:
| genchy (napisa): | Evo nastavljam s zadacima koje sam ostao duzan:
Radi se o trecem iz 2. zadace, naime, objasnit cu koncept, a detaljan raspis ostavljam vama, ako ce trebat i za demonstrature u petak.
Krenemo prema uputi, dakle trazimo potprostore 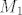 i i 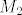 te te  iz kojeg zakljucujemo mogucnost trazenog raspisa. iz kojeg zakljucujemo mogucnost trazenog raspisa.
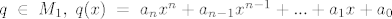 , a iz uvjeta , a iz uvjeta 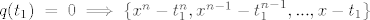 baza za baza za 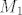 . Analogno za potprostor . Analogno za potprostor 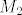 , pa imamo bazu za , pa imamo bazu za  , npr. , npr. 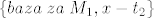 , znaci , znaci 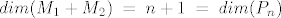 i zakljucujemo kako je trazeni raspis moguc, no nikako nije jedinstven, jer je i zakljucujemo kako je trazeni raspis moguc, no nikako nije jedinstven, jer je 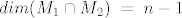 . . |
E, hvala ti puno čovječe, sada mi je taj zadatak jasan potpuno, kada sam pročitao sve tvoje postove vezane za taj zadatak.
Added after 39 minutes:
| 888 (napisa): | | jel možeš malo detaljnije objasnit kako si našao bazu za M+L, nije mi jasno zašto {baza za M,x-t2} i ovo zadnje zašto je M1 presjek M2=n-1... |
Ukoliko sam ja to shvatio, onda prema genchyu, dodaš jedan vektor iz baze za M2 u M1 i provjeriš je li to linearno nezavisan skup, budući da je dim(M1)=dim(M2)=n čim dodaš još jedan vektor u M1, ako su oni potom linearno nezavisni svi iz baze M1, s npr, tim x-t2 slijedi da M1+M2 je baza i razapinje cijeli P_n jer je dim(M1+M2)=n+1 kao i P_n.
A ja sam to sebi pojasnio(čitaj dalje:PO MOJEM MIŠLJENJU) tako što je to moguće samo zbog tog početnog uvjeta zadatka koji nam kaže da je t1!=t2, pa sam si razmišljao ovako, postoji li neki broj npr. a€R takav da je u a(x-t1)=x-t2, pa sam uvrstio brojeve jer je t1 različit od t2 ovako:
a(x-t1)=x-t2;t1=3,t2=4;
a(x-3)=x-4 i dobijemo
ax-3a=x-4 (po tm o jednakosti polinoma, oni su jednaki
ako i samo ako su im svi koeficijenti jednaki)
no to povlači da bi istovremeno moralo biti a=1 i a=4/3 a to je ⇒⇐ kontradikcija, ako nisam negdje pogrijesio u razmisljanju.
Također, sigurno ne postoji neki niz a_i eva iz R takvih da bi x-t2 bio linearna kombinacija vektora baze za M1 koji sadrze i polinome stp veceg od 1.I onda se vidi čak da je bilo t1=t2 u uvjetu zadatka da to ne bi bilo moguće reći.
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
|





