| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 2:19 pet, 17. 12. 2010 Naslov: Postano: 2:19 pet, 17. 12. 2010 Naslov: |
    |
|
|
Zelimo ocijeniti izraz sh(n)+th(n).
Sad malo pogledamo sto znamo o ovim funkcijama i uocimo [latex]0\leq th(n) < 1, \forall n \in \mathbb{N}[/latex]
Intuitivno, kad na to sve stavimo n-ti korijen, jasno je da taj izraz, manji od 1, nece previse utjecati na limes. Takodjer, po definiciji funkcije sh imamo,
kao sto je Tomislav rekao, [latex]sh(n)=\frac{e^n-e^{-n}}{2}[/latex].
Sad je dovoljno primjeniti dosta grube ograde, jer ce n-ti korijen "ponistiti" sve sto nije neka n-ta potencija. Zato mozemo reci, npr,
[latex]\frac{e^n}{2} - \frac{e^{-n}}{2}+th(n)\leq \frac{e^n}{2} - \frac{e^{-n}}{2}+1 \leq \frac{e^n}{2} + \frac{e^{n}}{2}= e^n [/latex].
(ovdje smo koristili ocitu nejednakost [latex]\frac{e^n}{2} \geq 1-\frac{e^{-n}}{2}[/latex], vrijedi za sve n jer je desna strana manja od 1)
Odozdo ogranicimo slicno:
[latex]\frac{e^n}{2} - \frac{e^{-n}}{2}+th(n) \geq \frac{e^n}{2}-\frac{e^n}{4} = \frac{e^n}{4}[/latex]
(Koristimo [latex]- \frac{e^n}{4} \leq th(n) -\frac{e^{-n}}{2}[/latex], sto vrijedi za sve malo vece n-ove; vrijedi jer je desna strana uvijek veca od -1, a -e^n/4 je za skoro sve n manji od -1)
Ove ograde se mozda cine malo random, al zapravo ih namjestis prema onome sto zelis dobiti (a cilj nam je ovdje postici e^n, uz eventualno neki koeficijent, jer znamo kako n-ti korijen djeluje na to)
Sada smo dobili [latex]\frac{e^n}{4} \leq sh(n) + th(n) \leq e^n[/latex]. Na to primjenimo n-ti korijen, pustimo na limes i dobijemo da ovaj pocetni izraz tezi u e.
Zelimo ocijeniti izraz sh(n)+th(n).
Sad malo pogledamo sto znamo o ovim funkcijama i uocimo 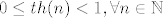
Intuitivno, kad na to sve stavimo n-ti korijen, jasno je da taj izraz, manji od 1, nece previse utjecati na limes. Takodjer, po definiciji funkcije sh imamo,
kao sto je Tomislav rekao, 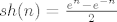 . .
Sad je dovoljno primjeniti dosta grube ograde, jer ce n-ti korijen "ponistiti" sve sto nije neka n-ta potencija. Zato mozemo reci, npr,
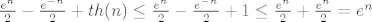 . .
(ovdje smo koristili ocitu nejednakost 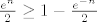 , vrijedi za sve n jer je desna strana manja od 1) , vrijedi za sve n jer je desna strana manja od 1)
Odozdo ogranicimo slicno:
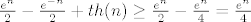
(Koristimo 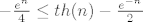 , sto vrijedi za sve malo vece n-ove; vrijedi jer je desna strana uvijek veca od -1, a -e^n/4 je za skoro sve n manji od -1) , sto vrijedi za sve malo vece n-ove; vrijedi jer je desna strana uvijek veca od -1, a -e^n/4 je za skoro sve n manji od -1)
Ove ograde se mozda cine malo random, al zapravo ih namjestis prema onome sto zelis dobiti (a cilj nam je ovdje postici e^n, uz eventualno neki koeficijent, jer znamo kako n-ti korijen djeluje na to)
Sada smo dobili 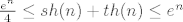 . Na to primjenimo n-ti korijen, pustimo na limes i dobijemo da ovaj pocetni izraz tezi u e. . Na to primjenimo n-ti korijen, pustimo na limes i dobijemo da ovaj pocetni izraz tezi u e.
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 10:46 sub, 18. 12. 2010 Naslov: Postano: 10:46 sub, 18. 12. 2010 Naslov: |
    |
|
|
Nije težak. :)
Primijeti da vrijedi [latex]-\displaystyle\frac{\pi}{2}<\arctan n<\displaystyle\frac{\pi}{2}[/latex]. (Zapravo, u ovom je slučaju arkus tangens uvijek pozitivan, ali nebitno... ovo nam je sasvim dovoljno).
Dakle, vrijedi [latex]-\displaystyle\frac{\pi}{2}+\cosh n<\arctan n +\cosh n<\displaystyle\frac{\pi}{2}+\cosh n[/latex]. E sad, znaš da se kosinus hiperbolni uglavnom za velike [latex]n[/latex] "ponaša kao" [latex]e^n[/latex], pa nam je to ideja tu.
S jedne strane, vrijedi (samo praktički koristimo definiciju kosinusa hiperbolnog) [latex]-\displaystyle\frac{\pi}{2}+\cosh n>\displaystyle\frac{e^n-\pi}{2}>\displaystyle\frac{e^n}{4}[/latex] (ova zadnja nejednakost vrijedi ako je [latex]n\geq 2[/latex], ali to nam ne igra ulogu jer [latex]n\to +\infty[/latex]). Sličnu stvar radimo s druge strane: [latex]\displaystyle\frac{\pi}{2}+\cosh n<\frac{\pi}{2}+e^n<2e^n[/latex] (ove ograde su vrlo grube, ali sasvim dovoljno za ono što radimo: bitno nam je da imamo neko ograničenje oblika [latex]Ce^n[/latex] za neku (recimo pozitivnu) konstantu [latex]C[/latex].
Dakle, sve zajedno, [latex]\displaystyle\frac{e^n}{4}<\arctan n +\cosh n<2e^n[/latex]. Stoga, [latex]\displaystyle\frac{e}{\sqrt[n]{4}}<\sqrt[n]{\arctan n +\cosh n}<e\sqrt[n]{2}[/latex]. Sad po teoremu o sendviču trivijalno zaključujemo da [latex]\sqrt[n]{\arctan n +\cosh n}\to e[/latex].
Evo, pitaj ako što nije jasno. :)
---
Ah, nisam uvidio CROmpirov zadatak. Uglavnom, čovjeku se uglavnom na početku čini da će biti nešto u stilu [latex]\displaystyle\frac{a^x-1}{x}[/latex], što je limes koji imate u tablici. Zapravo, i bit će, ali ne direktno - samo primijeti da je gornji izraz zapravo kvadrat: [latex]4^x+4^{-x}-2=(2^x-2^{-x})^2[/latex]. (Ima možda i pametniji način, da se odmah iz brojnika izluči [latex]2^{-x}[/latex], ali ovako-onako je stvar ista. :))
U svakom slučaju, sad nas zapravo zanima limes od [latex]\displaystyle\frac{2^x-2^{-x}}{x}[/latex], a onda će nam završni limes biti kvadrat ovoga. No, to nije teško: [latex]\displaystyle\frac{2^x-2^{-x}}{x}=\frac{4^x-1}{x}\cdot 2^{-x}[/latex]. Sad smo gotovi: znamo da [latex]2^{-x}\to 1[/latex], a [latex]\displaystyle\frac{4^x-1}{x}\to \ln 4[/latex] je poznati limes.
Dakle, [latex]\displaystyle\frac{2^x-2^{-x}}{x}\to \ln 4\cdot 1=\ln 4[/latex], pa je naš početni limes [latex]\ln^2 4[/latex]. (Nadam se da se dobro sjećam tzv. tabličnih limesa. Također se nadam da će se smajlići u nekom trenutku povratiti u svoju vulgaris verziju, no to je već druga stvar... :D)
Nije težak. 
Primijeti da vrijedi 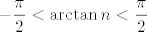 . (Zapravo, u ovom je slučaju arkus tangens uvijek pozitivan, ali nebitno... ovo nam je sasvim dovoljno). . (Zapravo, u ovom je slučaju arkus tangens uvijek pozitivan, ali nebitno... ovo nam je sasvim dovoljno).
Dakle, vrijedi 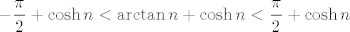 . E sad, znaš da se kosinus hiperbolni uglavnom za velike . E sad, znaš da se kosinus hiperbolni uglavnom za velike  "ponaša kao" "ponaša kao" 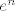 , pa nam je to ideja tu. , pa nam je to ideja tu.
S jedne strane, vrijedi (samo praktički koristimo definiciju kosinusa hiperbolnog) 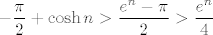 (ova zadnja nejednakost vrijedi ako je (ova zadnja nejednakost vrijedi ako je 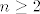 , ali to nam ne igra ulogu jer , ali to nam ne igra ulogu jer 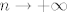 ). Sličnu stvar radimo s druge strane: ). Sličnu stvar radimo s druge strane: 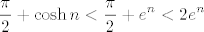 (ove ograde su vrlo grube, ali sasvim dovoljno za ono što radimo: bitno nam je da imamo neko ograničenje oblika (ove ograde su vrlo grube, ali sasvim dovoljno za ono što radimo: bitno nam je da imamo neko ograničenje oblika 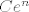 za neku (recimo pozitivnu) konstantu za neku (recimo pozitivnu) konstantu  . .
Dakle, sve zajedno, 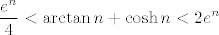 . Stoga, . Stoga, 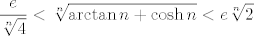 . Sad po teoremu o sendviču trivijalno zaključujemo da . Sad po teoremu o sendviču trivijalno zaključujemo da 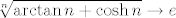 . .
Evo, pitaj ako što nije jasno. 
—
Ah, nisam uvidio CROmpirov zadatak. Uglavnom, čovjeku se uglavnom na početku čini da će biti nešto u stilu 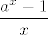 , što je limes koji imate u tablici. Zapravo, i bit će, ali ne direktno - samo primijeti da je gornji izraz zapravo kvadrat: , što je limes koji imate u tablici. Zapravo, i bit će, ali ne direktno - samo primijeti da je gornji izraz zapravo kvadrat: 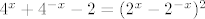 . (Ima možda i pametniji način, da se odmah iz brojnika izluči . (Ima možda i pametniji način, da se odmah iz brojnika izluči  , ali ovako-onako je stvar ista. , ali ovako-onako je stvar ista.  ) )
U svakom slučaju, sad nas zapravo zanima limes od 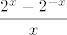 , a onda će nam završni limes biti kvadrat ovoga. No, to nije teško: , a onda će nam završni limes biti kvadrat ovoga. No, to nije teško: 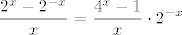 . Sad smo gotovi: znamo da . Sad smo gotovi: znamo da 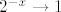 , a , a 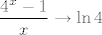 je poznati limes. je poznati limes.
Dakle, 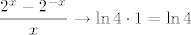 , pa je naš početni limes , pa je naš početni limes 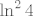 . (Nadam se da se dobro sjećam tzv. tabličnih limesa. Također se nadam da će se smajlići u nekom trenutku povratiti u svoju vulgaris verziju, no to je već druga stvar... . (Nadam se da se dobro sjećam tzv. tabličnih limesa. Također se nadam da će se smajlići u nekom trenutku povratiti u svoju vulgaris verziju, no to je već druga stvar...  ) )
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
|









