| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
Bruno^_^
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (20:22:27)
Postovi: (1D)16
|
 Postano: 18:17 sub, 8. 1. 2011 Naslov: Postano: 18:17 sub, 8. 1. 2011 Naslov: |
    |
|
|
[quote="mornik"]Ma bezveze je. :P
Samo koristi da je [latex]\displaystyle 1-\sqrt[m]{\cos(x)}=\frac{1-\cos(x)}{1+\sqrt[m]{\cos(x)}+\sqrt[m]{\cos^2(x)}+\ldots+\sqrt[m]{\cos^{m-1}(x)}}[/latex]. Budući da znaš limes od [latex]\displaystyle\frac{1-\cos(x)}{x^2}[/latex], a [latex]1+\sqrt[m]{\cos(x)}+\sqrt[m]{\cos^2(x)}+\ldots+\sqrt[m]{\cos^{m-1}(x)}[/latex] ima [latex]m[/latex] članova koji svi idu u [latex]1[/latex], dokaz je gotov. :)
(A baš si mogla i sama probati. :P Mislim, brže bi dobila odgovor. :D)[/quote]
Dokaz je jasan, no kako dokazati da isto vrijedi za recimo Pi? Tipa, odredite limes od [latex]\frac{1-cos(x)^\pi}{x^2}[/latex]. Ovdje se vidi da je limes (kada x ide u 0) Pi/2, no kako to formalno dokazati? :?
Ideja je naci 1-cos^(m1/n1) ( x ) / (x^2) <= (1 - cos^Pi ( x ) / x^2) <= 1-cos^(m2/n2) ( x ) / (x^2) dva konvergentna niza koji teze Pi+ i Pi-, jel to valja?
| mornik (napisa): | Ma bezveze je. 
Samo koristi da je 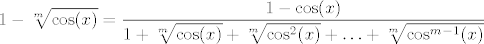 . Budući da znaš limes od . Budući da znaš limes od 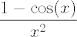 , a , a 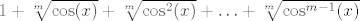 ima ima  članova koji svi idu u članova koji svi idu u  , dokaz je gotov. , dokaz je gotov. 
(A baš si mogla i sama probati.  Mislim, brže bi dobila odgovor. Mislim, brže bi dobila odgovor.  ) ) |
Dokaz je jasan, no kako dokazati da isto vrijedi za recimo Pi? Tipa, odredite limes od 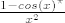 . Ovdje se vidi da je limes (kada x ide u 0) Pi/2, no kako to formalno dokazati? . Ovdje se vidi da je limes (kada x ide u 0) Pi/2, no kako to formalno dokazati? 
Ideja je naci 1-cos^(m1/n1) ( x ) / (x^2) ⇐ (1 - cos^Pi ( x ) / x^2) ⇐ 1-cos^(m2/n2) ( x ) / (x^2) dva konvergentna niza koji teze Pi+ i Pi-, jel to valja?
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:29 sub, 8. 1. 2011 Naslov: Postano: 21:29 sub, 8. 1. 2011 Naslov: |
    |
|
|
@Bruno^_^: Ideja je prirodna, vjerojatno i relativno hranjiva. Esencijalno, ti želiš dokazati da je [latex]f(y)[/latex] neprekidna funkcija, gdje je [latex]\displaystyle f(y):=\lim_{x\to 0}\frac{1-\cos^y(x)}{x^2}[/latex]. (S tim da bi još prije toga želio i tvrdnju dokazati za sve racionalne [latex]y[/latex], ali to ne bi trebalo biti preteško.)
Ali, gle, umjesto da sad pokušavamo raditi na tome, ima stvar koja se čini znatno smislenija u ovakvim slučajevima: L'Hôpital. Znam, gasp!, niste to još radili :), ali poanta je nekako u ovom zadatku s [latex]m[/latex]-tim korijenom bila naći taj zgodan trik. Ovdje zgodnog trika (kakvi se forsiraju u kolokvijima u MA1, koliko vidim) vrlo vjerojatno nema, pa bismo time da pokušamo izbjeći L'Hôpitala (i time učinimo zadatak ljepšim) dobili vjerojatno puno tehničkog računa (mislim, pretpostavljam - čisto valja primijetiti da ti zapravo gore ne govoriš o uobičajenom teoremu o sendviču, nego nečemu što uključuje limes limesa), što bi opet poružnilo zadatak. Dakle, ako je zadatak čisto za tvoju zabavu (a izgleda mi kao da je :P), moja je preporuka L'Hôpital. Ako treba, prođemo kroz rješenje - zbilja je dva reda.
@ceps: Pa ovo je ogavno. :D Malo sam u stisci s vremenom, a moraš i ti nešto napraviti barem :D, pa ću samo dati neko okvirno rješenje. Riješio sam zadatak, ali za napisati ga jednadžbu po jednadžbu bi mi trebalo neko vrijeme, tako da pitaj ako nešto smrdi. Ne jamčim da je ovo najljepša verzija - vjerojatno i nije, ali je jedina koje se moj bizaran um sjetio:
1. korak: Utvrdi (teorem o sendviču) da [latex]\displaystyle\frac{\ln(x^2+3x+4)}{\ln(x^2+2x+3)}\to 1[/latex].
Dakle, sad znaš da imaš nešto oblika [latex]1^{+\infty}[/latex]. Stoga, koristimo onaj limes iz tablice da objavimo da je naš limes zapravo [latex]\displaystyle e^{x\ln(x)(\frac{\ln(x^2+3x+4)}{\ln(x^2+2x+3)}-1)}[/latex].
2. korak: Utvrđujemo limes od [latex]\displaystyle x\ln(x)(\frac{\ln(x^2+3x+4)}{\ln(x^2+2x+3)}-1)[/latex] Kad to raspišemo, dobivamo da tražimo limes od [latex]\displaystyle \frac{\ln(x)}{\ln(x^2+2x+3)}\cdot \ln(1+\frac{x+1}{x^2+2x+3})\cdot x[/latex].
3. korak: Limes ovog prvog razlomka gore je [latex]0.5[/latex] - možeš ponovno ići po teoremu o sendviču, recimo (koristeći [latex]0.5\cdot \ln(0.5\cdot (x^2+2x+3))<\ln(x)<0.5\cdot\ln(x^2+2x+3)[/latex], na primjer). U drugom dijelu, [latex]\displaystyle \frac{x+1}{x^2+2x+3}\to 0[/latex], pa koristimo [latex]\displaystyle\frac{\ln(1+t)}{t}[/latex] za [latex]t\to 0[/latex]. Dakle, rearanžiramo ovaj drugi dio kao [latex]\frac{\ln(1+\frac{x+1}{x^2+2x+3})}{\frac{x+1}{x^2+2x+3}}\cdot x\frac{x+1}{x^2+2x+3}[/latex]. Sad si gotov - limes i prvog i drugog dijela ovog izraza gore je očito [latex]1[/latex].
Stoga, finalno je rješenje, nadajmo se, [latex]\sqrt{e}[/latex]. :)
[size=9](Inače, nepovezano s ovim, ali ako te veseli: inače svi volimo provjeravati jesmo li ovakve limese dobro izračunali tako da uvrstimo neki veliki broj ("blizu beskonačnosti"), pa onda gledamo je li to otprilike jednako ovome što mislimo da je limes, jel tak? :D E, pa [url=http://www.google.hr/search?hl=en&q=%28ln%2810%5E40%2B3%2A10%5E20%2B4%29%2Fln%2810%5E40%2B2%2A10%5E20%2B3%29%29%5E%28ln%2810%5E20%29%2A10%5E20%29]ovaj[/url] izračun je živi dokaz (ima i puno jednostavnijih, doduše) da ne treba slijepo vjerovati kompjutoru. :D (Naravno, i za sve veće [latex]x[/latex], situacija je ista.) Razlog je, naravno, u "prikazivosti" realnih brojeva... da ne tupim sad. :D Doduše (naravno), WolframAlpha je [url=http://www.wolframalpha.com/input/?i=%28ln%2810%5E120%2B3%2A10%5E60%2B4%29%2Fln%2810%5E120%2B2%2A10%5E60%2B3%29%29%5E%28ln%2810%5E60%29%2A10%5E60%29]tu[/url] znatno pametniji.)[/size]
EDIT: Glupost u mom sveopćem pametovanju. Sorry. :oops:
@Bruno^_^: Ideja je prirodna, vjerojatno i relativno hranjiva. Esencijalno, ti želiš dokazati da je 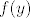 neprekidna funkcija, gdje je neprekidna funkcija, gdje je 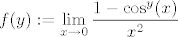 . (S tim da bi još prije toga želio i tvrdnju dokazati za sve racionalne . (S tim da bi još prije toga želio i tvrdnju dokazati za sve racionalne  , ali to ne bi trebalo biti preteško.) , ali to ne bi trebalo biti preteško.)
Ali, gle, umjesto da sad pokušavamo raditi na tome, ima stvar koja se čini znatno smislenija u ovakvim slučajevima: L'Hôpital. Znam, gasp!, niste to još radili  , ali poanta je nekako u ovom zadatku s , ali poanta je nekako u ovom zadatku s  -tim korijenom bila naći taj zgodan trik. Ovdje zgodnog trika (kakvi se forsiraju u kolokvijima u MA1, koliko vidim) vrlo vjerojatno nema, pa bismo time da pokušamo izbjeći L'Hôpitala (i time učinimo zadatak ljepšim) dobili vjerojatno puno tehničkog računa (mislim, pretpostavljam - čisto valja primijetiti da ti zapravo gore ne govoriš o uobičajenom teoremu o sendviču, nego nečemu što uključuje limes limesa), što bi opet poružnilo zadatak. Dakle, ako je zadatak čisto za tvoju zabavu (a izgleda mi kao da je -tim korijenom bila naći taj zgodan trik. Ovdje zgodnog trika (kakvi se forsiraju u kolokvijima u MA1, koliko vidim) vrlo vjerojatno nema, pa bismo time da pokušamo izbjeći L'Hôpitala (i time učinimo zadatak ljepšim) dobili vjerojatno puno tehničkog računa (mislim, pretpostavljam - čisto valja primijetiti da ti zapravo gore ne govoriš o uobičajenom teoremu o sendviču, nego nečemu što uključuje limes limesa), što bi opet poružnilo zadatak. Dakle, ako je zadatak čisto za tvoju zabavu (a izgleda mi kao da je  ), moja je preporuka L'Hôpital. Ako treba, prođemo kroz rješenje - zbilja je dva reda. ), moja je preporuka L'Hôpital. Ako treba, prođemo kroz rješenje - zbilja je dva reda.
@ceps: Pa ovo je ogavno.  Malo sam u stisci s vremenom, a moraš i ti nešto napraviti barem Malo sam u stisci s vremenom, a moraš i ti nešto napraviti barem  , pa ću samo dati neko okvirno rješenje. Riješio sam zadatak, ali za napisati ga jednadžbu po jednadžbu bi mi trebalo neko vrijeme, tako da pitaj ako nešto smrdi. Ne jamčim da je ovo najljepša verzija - vjerojatno i nije, ali je jedina koje se moj bizaran um sjetio: , pa ću samo dati neko okvirno rješenje. Riješio sam zadatak, ali za napisati ga jednadžbu po jednadžbu bi mi trebalo neko vrijeme, tako da pitaj ako nešto smrdi. Ne jamčim da je ovo najljepša verzija - vjerojatno i nije, ali je jedina koje se moj bizaran um sjetio:
1. korak: Utvrdi (teorem o sendviču) da 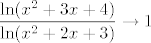 . .
Dakle, sad znaš da imaš nešto oblika 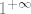 . Stoga, koristimo onaj limes iz tablice da objavimo da je naš limes zapravo . Stoga, koristimo onaj limes iz tablice da objavimo da je naš limes zapravo 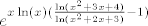 . .
2. korak: Utvrđujemo limes od 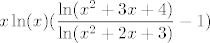 Kad to raspišemo, dobivamo da tražimo limes od Kad to raspišemo, dobivamo da tražimo limes od 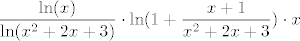 . .
3. korak: Limes ovog prvog razlomka gore je 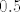 - možeš ponovno ići po teoremu o sendviču, recimo (koristeći - možeš ponovno ići po teoremu o sendviču, recimo (koristeći  , na primjer). U drugom dijelu, , na primjer). U drugom dijelu, 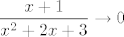 , pa koristimo , pa koristimo  za za 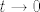 . Dakle, rearanžiramo ovaj drugi dio kao . Dakle, rearanžiramo ovaj drugi dio kao 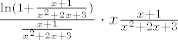 . Sad si gotov - limes i prvog i drugog dijela ovog izraza gore je očito . Sad si gotov - limes i prvog i drugog dijela ovog izraza gore je očito  . .
Stoga, finalno je rješenje, nadajmo se, 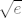 . . 
(Inače, nepovezano s ovim, ali ako te veseli: inače svi volimo provjeravati jesmo li ovakve limese dobro izračunali tako da uvrstimo neki veliki broj ("blizu beskonačnosti"), pa onda gledamo je li to otprilike jednako ovome što mislimo da je limes, jel tak?  E, pa ovaj izračun je živi dokaz (ima i puno jednostavnijih, doduše) da ne treba slijepo vjerovati kompjutoru. E, pa ovaj izračun je živi dokaz (ima i puno jednostavnijih, doduše) da ne treba slijepo vjerovati kompjutoru.  (Naravno, i za sve veće (Naravno, i za sve veće  , situacija je ista.) Razlog je, naravno, u "prikazivosti" realnih brojeva... da ne tupim sad. , situacija je ista.) Razlog je, naravno, u "prikazivosti" realnih brojeva... da ne tupim sad.  Doduše (naravno), WolframAlpha je tu znatno pametniji.) Doduše (naravno), WolframAlpha je tu znatno pametniji.)
EDIT: Glupost u mom sveopćem pametovanju. Sorry. 
Zadnja promjena: mornik; 21:57 sub, 8. 1. 2011; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 21:41 sub, 8. 1. 2011 Naslov: Postano: 21:41 sub, 8. 1. 2011 Naslov: |
    |
|
|
Hvala! Puno je pomoglo, ma skužio sam ovaj 1. korak sam, a skoro i 2... haha...
Samo jedno malo pitanje:
[latex]\frac{\ln(x)}{\ln(x^2+2x+3)}[/latex] za ovaj dio, ja sam se vodio logikom da se kako x ide u beskonačnost za ''dovoljno velike'' x ovaj [latex]x^2+2x+3[/latex] ponaša kao [latex]x^2[/latex]...
pa to izgleda kao [latex]\frac{ln x}{2lnx} = 0.5[/latex].
E sad, da li je na kolokviju dovoljno to tako napisati ili je ipak potrebno dokazivati, ovako pomoću teorema o sendviču?
Hvala! Puno je pomoglo, ma skužio sam ovaj 1. korak sam, a skoro i 2... haha...
Samo jedno malo pitanje:
 za ovaj dio, ja sam se vodio logikom da se kako x ide u beskonačnost za ''dovoljno velike'' x ovaj za ovaj dio, ja sam se vodio logikom da se kako x ide u beskonačnost za ''dovoljno velike'' x ovaj  ponaša kao ponaša kao 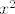 ... ...
pa to izgleda kao 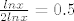 . .
E sad, da li je na kolokviju dovoljno to tako napisati ili je ipak potrebno dokazivati, ovako pomoću teorema o sendviču?
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:49 sub, 8. 1. 2011 Naslov: Postano: 21:49 sub, 8. 1. 2011 Naslov: |
    |
|
|
Ha čuj, da sam na tvom mjestu, ja bih takvu stvar pisao. Naravno, logika je jasna, ali, mislim, baš to znanje (među ostalim, teorema o sendviču) se i ispituje na kolokviju... :D Ima sigurno neki jednostavniji postupak za teorem o sendviču od "mojega" - recimo, [latex]x^2<x^2+2x+3<2x^2[/latex] bi trebao biti OK.
Ha čuj, da sam na tvom mjestu, ja bih takvu stvar pisao. Naravno, logika je jasna, ali, mislim, baš to znanje (među ostalim, teorema o sendviču) se i ispituje na kolokviju...  Ima sigurno neki jednostavniji postupak za teorem o sendviču od "mojega" - recimo, Ima sigurno neki jednostavniji postupak za teorem o sendviču od "mojega" - recimo, 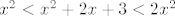 bi trebao biti OK. bi trebao biti OK.
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 15:48 ned, 9. 1. 2011 Naslov: Postano: 15:48 ned, 9. 1. 2011 Naslov: |
    |
|
|
@A-tom: Bez brige, evo jednog rješenja koje nije preko teorema o sendviču. ;)
Definirajmo niz [latex]a_{n}:=\prod^{n}_{i=1}\left(\sqrt{2}-\sqrt[2i+1]{2})[/latex]. Uočimo da tada tražimo [latex]\displaystyle\lim_{x\to +\infty}a_n[/latex].
Ovaj zapis je koristan jer tada znamo da je [latex]a_n = (\sqrt{2}-\sqrt[2n+1]{2})\cdot a_{n-1}[/latex].
Dalje se zadatak rješava na sličan način kao i ostali zadaci s rekurzivnim nizovima iz kolokvija. Ako ne znaš kako, evo ti još jedan hint: probaj dokazati monotonost niza i ograničenost niza s odgovarajuće strane (odozgo ili odozdo). Tada po teoremu znaš da je konvergentan i limes tražiš po rekurzivnoj relaciji.
@Joker: Kada si raspisala po potencijama, onda si dobila izraz [latex]\frac{2\sqrt[n]{3}}{n(\sqrt[n]{3}-1)}[/latex], zar ne? Izraz u brojniku nam odgovara, a u nazivniku imamo "poznati" izraz: [latex]\sqrt[n]{3}-1 = 3^{\frac{1}{n}}-1[/latex], a [latex]\frac{1}{n}[/latex] teži u nulu... Nadam se da ti je sada poznato što raditi. :D
Kada i taj izraz "dotjeraš", ostane ti samo ovaj [latex]n[/latex] u nazivniku. Ali on će se zapravo "poništiti" kada središ prethodno navedeni izraz! Naime, [latex]n = \frac{1}{\frac{1}{n}}[/latex].
Inače, Stolzov teorem možda i vrijedi za ovaj zadatak, ali zapis izraza u brojniku nije ekvivalentan onome kojeg je A-tom napisala. Naime, tada ti ostaje [latex]\sum^{n+1}_{i=1}3^{\frac{i}{n+1}}-\sum^{n}_{i=1}3^{\frac{i}{n}}[/latex], a to, na žalost, nije "skrativo".
(Vjerovatno si mislila da su nazivnici u eksponentu jednaki, zar ne? :))
@A-tom: Bez brige, evo jednog rješenja koje nije preko teorema o sendviču. 
Definirajmo niz  . Uočimo da tada tražimo . Uočimo da tada tražimo  . .
Ovaj zapis je koristan jer tada znamo da je  . .
Dalje se zadatak rješava na sličan način kao i ostali zadaci s rekurzivnim nizovima iz kolokvija. Ako ne znaš kako, evo ti još jedan hint: probaj dokazati monotonost niza i ograničenost niza s odgovarajuće strane (odozgo ili odozdo). Tada po teoremu znaš da je konvergentan i limes tražiš po rekurzivnoj relaciji.
@Joker: Kada si raspisala po potencijama, onda si dobila izraz  , zar ne? Izraz u brojniku nam odgovara, a u nazivniku imamo "poznati" izraz: , zar ne? Izraz u brojniku nam odgovara, a u nazivniku imamo "poznati" izraz:  , a , a  teži u nulu... Nadam se da ti je sada poznato što raditi. teži u nulu... Nadam se da ti je sada poznato što raditi. 
Kada i taj izraz "dotjeraš", ostane ti samo ovaj  u nazivniku. Ali on će se zapravo "poništiti" kada središ prethodno navedeni izraz! Naime, u nazivniku. Ali on će se zapravo "poništiti" kada središ prethodno navedeni izraz! Naime,  . .
Inače, Stolzov teorem možda i vrijedi za ovaj zadatak, ali zapis izraza u brojniku nije ekvivalentan onome kojeg je A-tom napisala. Naime, tada ti ostaje 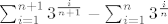 , a to, na žalost, nije "skrativo". , a to, na žalost, nije "skrativo".
(Vjerovatno si mislila da su nazivnici u eksponentu jednaki, zar ne?  ) )
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 10:12 pon, 10. 1. 2011 Naslov: Postano: 10:12 pon, 10. 1. 2011 Naslov: |
    |
|
|
Ne znam jesi li vidio stranicu-dvije ranije da zadatak (vjerojatno) ima grešku - nedostaje uvjet da su [latex]f[/latex] i [latex]g[/latex] neprekidne, pa se može naći kontraprimjer (ukratko, [latex]f(0)=1[/latex], [latex]f(x)=0[/latex] za [latex]x>0[/latex] i [latex]g(x)=x[/latex]).
Ako si vidio, a i dalje te stvar muči, onda s ponosom predstavljam ovo. :D Neke ideje su, hm, možda malo neortodoksne, tako da sam siguran da će se u nekom trenutku pojaviti i jednostavnije rješenje, ali 'ajde, zasad... :)
Dakle, u rješenju uzimamo da su ove funkcije neprekidne. Prvo pretpostavljamo suprotno. U tom slučaju, [latex]g-f[/latex] je također neprekidna funkcija. Kako ona nema nultočaka (upravo iz naše pretpostavke to "znamo"), vrijedi ili [latex](g-f)(x)>0[/latex] za sve [latex]x\in[0,1][/latex] ili [latex](g-f)(x)<0[/latex] za sve [latex]x\in[0,1][/latex]. (Dokaz toga je trivijalan: pretpostavi da postoje neki [latex]a, b[/latex] takvi da je [latex]g(a)-f(a)>0>g(b)-f(b)[/latex]. Onda po Bolzano-Weierstrassovom teoremu slijedi da negdje između [latex]a[/latex] i [latex]b[/latex] funkcija [latex]g-f[/latex] postiže i nulu. Kontradikcija.)
Dalje uzimamo bez smanjenja općenitosti prvi slučaj (primijeti da su [latex]f[/latex] i [latex]g[/latex] posve simetrične, pa će ovaj slučaj biti istovjetan drugome): [latex]g(x)>f(x)[/latex] svugdje u domeni.
E, sad, [latex]g-f[/latex] je, kao što smo rekli, neprekidna funkcija. Stoga, po Bolzano-Weierstrasovom teoremu znamo da ona na zatvorenom intervalu [latex][0,1][/latex] ima infimum koji se i postiže - zapravo, minimum. Neka je taj minimum [latex]m[/latex]. Iz prethodne diskusije znamo da je [latex]m>0[/latex].
Dakle, vrijedi [latex]g(x)\geq f(x)+m[/latex] za sve [latex]x\in[0,1][/latex]. OK. Sad još dolazi završni korak (taj je vjerojatno nekako najbizarniji za sjetiti se :D): dokazat ćemo indukcijom da za svaki [latex]n\in\mathbb{N}[/latex] vrijedi [latex]g^{[n]}(x)\geq f^{[n]}(x)+mn[/latex] za sve [latex]x\in[0,1][/latex], pri čemu je [latex]f^{[n]}:=f(f(\ldots(f(x))\ldots))[/latex] s [latex]n[/latex] "poziva" funkcije [latex]f[/latex], čisto da bude kraće pisati (naravno, analogno za [latex]g[/latex]).
Pa dobro, baza očito vrijedi - gore smo ju argumentirali. Sad pretpostavljamo da vrijedi [latex]g^{[n]}(x)\geq f^{[n]}(x)+mn[/latex] za neki [latex]n\in\mathbb{N}[/latex]. Umjesto [latex]x[/latex] uvrštavamo [latex]f(x)[/latex] (kako tvrdnja mora vrijediti za sve [latex]x\in[0,1][/latex], mora vrijediti i za sve [latex]f(x)[/latex] jer su i oni u tom intervalu). Dakle, [latex]g^{[n]}(f(x))\geq f^{[n+1]}(x)+mn[/latex]. Sad na lijevoj strani koristeći činjenicu da [latex]f[/latex] i [latex]g[/latex] komutiraju (ako hoćeš, ovo formalno isto možeš dokazati indukcijom, ali dosta je očito iz definicije [latex]g^{[n]}[/latex]) dobivamo da je to jednako [latex]f(g^{[n]}(x))[/latex]. Stoga, [latex]f(g^{[n]}(x))\geq f^{[n+1]}(x)+mn[/latex] za sve [latex]x\in[0,1][/latex]. E, sad koristimo tvrdnju koja je zapravo i baza ove indukcije (nju smo dokazali prije nego što smo ušli u indukciju, tako da s njenim korištenjem nemamo nikakvih problema): vrijedi [latex]g(t)\geq f(t)+m[/latex]. No dobro, uzmimo [latex]t:=g^{[n]}(x)\in[0,1][/latex]. Dakle, [latex]g^{[n+1]}(x)\geq f(g^{[n]}(x))+m[/latex] za sve [latex]x[/latex] iz domene.
U ovom trenutku smo završili: imamo [latex]g^{[n+1]}(x)\geq f(g^{[n]}(x))+m\geq f^{[n+1]}(x)+mn+m=f^{[n+1]}(x)+m(n+1)[/latex], čime smo legalno proveli korak indukcije. E, a sada zaključak direktno slijedi iz Arhimedovog aksioma: odaberimo [latex]n_0\in\mathbb{N}[/latex] takav da je [latex]mn_0>1[/latex]. U tom slučaju [latex]g^{[n_0]}(x)>f^{[n_0]}(x)+1[/latex] za svaki [latex]x[/latex] iz domene. No, to je nemoguće budući da su i [latex]f^{[n_0]}(x)[/latex] i [latex]g^{[n_0]}(x)[/latex] iz [latex][0,1][/latex], pa je njihova razlika najviše [latex]1[/latex].
Sve u svemu, došli smo do kontradikcije (naravno, postupak za [latex]f>g[/latex] je potpuno isti, to smo gore već argumentirali), a kako smo pretpostavili da tvrdnja zadatka ne vrijedi, ispada da ipak vrijedi. :P
Nadam se da je ovo točno... :)
Ne znam jesi li vidio stranicu-dvije ranije da zadatak (vjerojatno) ima grešku - nedostaje uvjet da su  i i  neprekidne, pa se može naći kontraprimjer (ukratko, neprekidne, pa se može naći kontraprimjer (ukratko, 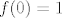 , , 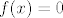 za za 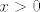 i i 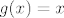 ). ).
Ako si vidio, a i dalje te stvar muči, onda s ponosom predstavljam ovo.  Neke ideje su, hm, možda malo neortodoksne, tako da sam siguran da će se u nekom trenutku pojaviti i jednostavnije rješenje, ali 'ajde, zasad... Neke ideje su, hm, možda malo neortodoksne, tako da sam siguran da će se u nekom trenutku pojaviti i jednostavnije rješenje, ali 'ajde, zasad... 
Dakle, u rješenju uzimamo da su ove funkcije neprekidne. Prvo pretpostavljamo suprotno. U tom slučaju,  je također neprekidna funkcija. Kako ona nema nultočaka (upravo iz naše pretpostavke to "znamo"), vrijedi ili je također neprekidna funkcija. Kako ona nema nultočaka (upravo iz naše pretpostavke to "znamo"), vrijedi ili 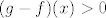 za sve za sve  ili ili 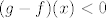 za sve za sve  . (Dokaz toga je trivijalan: pretpostavi da postoje neki . (Dokaz toga je trivijalan: pretpostavi da postoje neki 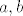 takvi da je takvi da je 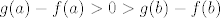 . Onda po Bolzano-Weierstrassovom teoremu slijedi da negdje između . Onda po Bolzano-Weierstrassovom teoremu slijedi da negdje između  i i 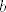 funkcija funkcija  postiže i nulu. Kontradikcija.) postiže i nulu. Kontradikcija.)
Dalje uzimamo bez smanjenja općenitosti prvi slučaj (primijeti da su  i i  posve simetrične, pa će ovaj slučaj biti istovjetan drugome): posve simetrične, pa će ovaj slučaj biti istovjetan drugome):  svugdje u domeni. svugdje u domeni.
E, sad,  je, kao što smo rekli, neprekidna funkcija. Stoga, po Bolzano-Weierstrasovom teoremu znamo da ona na zatvorenom intervalu je, kao što smo rekli, neprekidna funkcija. Stoga, po Bolzano-Weierstrasovom teoremu znamo da ona na zatvorenom intervalu 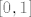 ima infimum koji se i postiže - zapravo, minimum. Neka je taj minimum ima infimum koji se i postiže - zapravo, minimum. Neka je taj minimum  . Iz prethodne diskusije znamo da je . Iz prethodne diskusije znamo da je 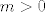 . .
Dakle, vrijedi 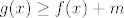 za sve za sve  . OK. Sad još dolazi završni korak (taj je vjerojatno nekako najbizarniji za sjetiti se . OK. Sad još dolazi završni korak (taj je vjerojatno nekako najbizarniji za sjetiti se  ): dokazat ćemo indukcijom da za svaki ): dokazat ćemo indukcijom da za svaki 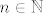 vrijedi vrijedi  za sve za sve  , pri čemu je , pri čemu je 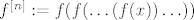 s s  "poziva" funkcije "poziva" funkcije  , čisto da bude kraće pisati (naravno, analogno za , čisto da bude kraće pisati (naravno, analogno za  ). ).
Pa dobro, baza očito vrijedi - gore smo ju argumentirali. Sad pretpostavljamo da vrijedi  za neki za neki 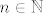 . Umjesto . Umjesto  uvrštavamo uvrštavamo 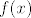 (kako tvrdnja mora vrijediti za sve (kako tvrdnja mora vrijediti za sve  , mora vrijediti i za sve , mora vrijediti i za sve 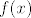 jer su i oni u tom intervalu). Dakle, jer su i oni u tom intervalu). Dakle, 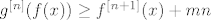 . Sad na lijevoj strani koristeći činjenicu da . Sad na lijevoj strani koristeći činjenicu da  i i  komutiraju (ako hoćeš, ovo formalno isto možeš dokazati indukcijom, ali dosta je očito iz definicije komutiraju (ako hoćeš, ovo formalno isto možeš dokazati indukcijom, ali dosta je očito iz definicije  ) dobivamo da je to jednako ) dobivamo da je to jednako 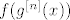 . Stoga, . Stoga,  za sve za sve  . E, sad koristimo tvrdnju koja je zapravo i baza ove indukcije (nju smo dokazali prije nego što smo ušli u indukciju, tako da s njenim korištenjem nemamo nikakvih problema): vrijedi . E, sad koristimo tvrdnju koja je zapravo i baza ove indukcije (nju smo dokazali prije nego što smo ušli u indukciju, tako da s njenim korištenjem nemamo nikakvih problema): vrijedi 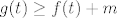 . No dobro, uzmimo . No dobro, uzmimo 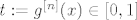 . Dakle, . Dakle, 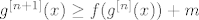 za sve za sve  iz domene. iz domene.
U ovom trenutku smo završili: imamo 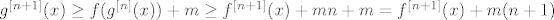 , čime smo legalno proveli korak indukcije. E, a sada zaključak direktno slijedi iz Arhimedovog aksioma: odaberimo , čime smo legalno proveli korak indukcije. E, a sada zaključak direktno slijedi iz Arhimedovog aksioma: odaberimo  takav da je takav da je  . U tom slučaju . U tom slučaju 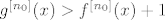 za svaki za svaki  iz domene. No, to je nemoguće budući da su i iz domene. No, to je nemoguće budući da su i 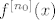 i i  iz iz 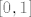 , pa je njihova razlika najviše , pa je njihova razlika najviše  . .
Sve u svemu, došli smo do kontradikcije (naravno, postupak za  je potpuno isti, to smo gore već argumentirali), a kako smo pretpostavili da tvrdnja zadatka ne vrijedi, ispada da ipak vrijedi. je potpuno isti, to smo gore već argumentirali), a kako smo pretpostavili da tvrdnja zadatka ne vrijedi, ispada da ipak vrijedi. 
Nadam se da je ovo točno... 
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
|













